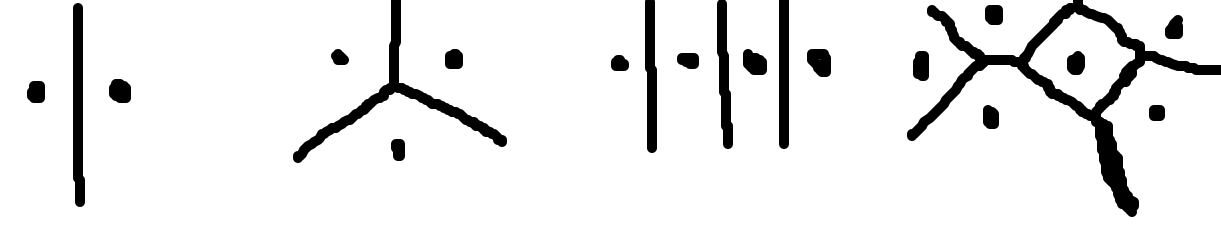Triangulating Polygons

Amongst most common kinds of meshes are those involving triangles.
For us a polygon will be a sequence of vertices in a list, with adjacent vertices in the list connected by edges, where the the first and last are connected, and no edges cross each other.
It is often useful to break a polygon into triangles for rendering. This is called triangulation.
For a convex polygon, this is easy, just add edges from the first point in the list to each other point in the list and this, together with the edges of the original polygon, will give a triangulation.
In order to triangulate a general polygon, we start with a polygon and succesively add edges between two of its vertices.
We now look at how to choose which two vertices.

Definition. A diagonal of a polygon `P` is a segment `\vec u \vecv` between two distinct vertices `vec u`, `vec v` of `P` whose interior is contained in `P`.

Diagonal Lemma

Every polygon `P` in `\mathbb{R}^2` with `n > 3` vertices has a diagonal.

Proof. Order the vertices of `P` by their x-coordinates and, of the left-most vertices, let `vec u` be the one with smallest y-coordinate. Let `vec v` and `vec w` be the two vertices of `P` adjacent to `vec u`. If `vec vw` is a diagonal we are done. Otherwise, let S be the set of vertices of `P` other than `vec u, vec v, vec w` that lie in the triangle `vec u vec v vecw`. Choose a vertex `vec u'` in `S` that is farthest from the line through `vec v`, `vec w`. We claim that `vec u vec u'` is a diagonal. To see this notice, that the line parallel to `vec v vec w` through `vec u'` divides the plane into two sides. The halfplane away from `vec u` must contain all the points of `S` and any edges between these points.

Triangulation Theorem

Every polygon can be triangulated. If the polygon has `n` vertices, then each of its triangulations will have `n-2` vertices.

Proof. Let `P` be a polygon in `mathbb{R}^2` with `n ≥ 3` vertices. The proof is by induction on `n`. The `n=3` case is trivial. For `n > 3` assume the theorem is true for all `3 \leq m < n`. By the previous lemma, `P` has a diagonal, and this diagonal divides `P` into two polygons, each have few than `n` vertices. Suppose `P_1, P_2` have respectively `n_1, n_2 < n` vertices. By induction, these polygons will have a triangulation on `n_1 -2` and `n_2 -2` vertices respectively. As `P_1, P_2` share two vertices we have `n_1 + n_2 = n + 2`. So the complete triangulation of `P` will have `n_1 -2 + n_2 -2 = n_1 + n_2 -4 = n - 2` vertices as desired.

The lemma and the theorem give an algorithm for doing triangulation, although it is quadratic. One can improve this to O(n log n) time with a little work.
We are next going to look at important ways that a collection of points in a space can be used to divide that space.
One of these ways will give another kind of way to do triangulation.

Voronoi Diagrams

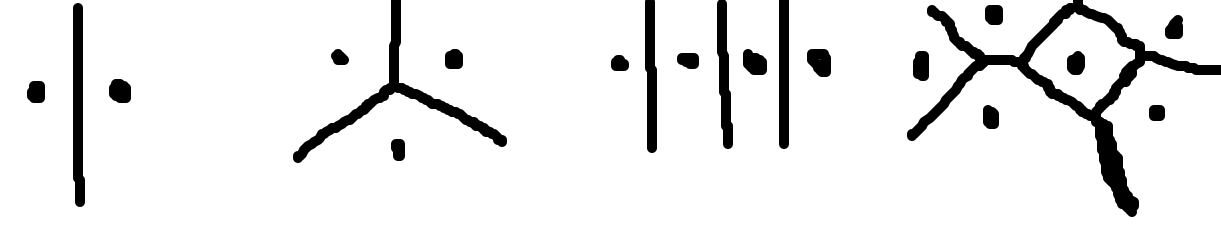
Let `S` be a set of points in a metric space `X` (a space with a distance function satisfying the triangle inequality).
Each point `vec p` in `S` defines a Voronoi cell of those points in `X` which are at least as close to `vec p` as any other `vec p'` in `S`.
Let `text{Vor}(S)`, the Voronoi Diagram of S, denote the set of Voronoi cells of points in `S`.
The above picture shows some examples of Voronoi diagrams: for two and three points, for co-linear points, as well as for a more general figure.
Voronoi diagrams are useful in databases for answering nearest neighbor queries with respect to a set of points. For instance, which is the nearest hospital to somewhere?
Voronoi Diagrams can be used to model many things.
For example, imagine you randomly dispersed tree seeds in a terrain.
Then you allowed the trees to grow to occupy as much space as possible, provided they don't "mess" with the other trees. This gives some kind of Voronoi diagram.
By taking the points `S` to be periodic in the plane (say some kind of lattice), the associated Voronoi diagram often looks like an interesting tiling of the plane.
If our points `S` are defining the boundary of an object, generalizing the notion of Voronoi diagram to non-discrete sets, then the Voronoi diagram is essentially giving the medial axis representation.

Delauney Triangulation

An example Delauney Graph which isn't a triangulation

Given a set of points `S` in the plane. The Delauney graph of `S` consists of the vertices of `S`, together with the edge set where there is an edge between `v` and `u` in `S` iff the Voronoi cells associated to those vertices share a common edge.
The Delauney Cell complex of `S` is the 2D-cell complex defined by the condition that its vertices and edges of each cell are vertices and edges of the Delauney graph.
2-cells in a Delauney Cell complex are called faces.
Voronoi diagrams and Delauney graphs are dual to each other: A Voronoi cell in a diagram `D` can be viewed a vertex in the Delauney Graph `G`. A vertex in `D` can be viewed as a cell `G` given by the edges in `G` which are crossed by edges from `D`.
Edges of the Delauney Triangulation will be orthogonal to the edges of the shared Voronoi cells.
It turns out if no four points of `S` lie on a circle, then each face of the Delauney cell complex is a triangle.
Otherwise, one can subdivide the faces into triangles to get a Delauney Triangulation.
One application of this is that if one have a terrain specified by the elevation values of a set of points, one natural way to get a mesh for this is to look at the Delauney Triangulation.
Three points of `S` are vertices of the same face of the Delauney cell complex iff the circle defined by them contains no point of `S` in its interior.
This gives us a way to find the largest empty circles amongst a set of points: Delauney triangulate and look for the cell that defines the largest circle.

Why the Delauney Triangulation is a Good Triangulation

Theorem Let `S` be a finite set of points in the plane and let `K` be a triangulation of `S`. Then `K` is a Delauney Triangulation iff the circle circumscribing any triangle in `K` does not contain any point `S` in its interior.

Definition. Let `S` be a finite set of points in the plane and let `K` be a triangulation of `S`. Suppose `K` has `m` triangles and order the `3m` angles `a_i` of these triangles in increasing order to create a so-called "angle vector": `(a_1, \ldots, a_(3m))`. The triangulation is called angle-optimal for `S` if `(a_1, \ldots, a_(3m)) \geq (b_1, \ldots, b_(3m))` for any other triangulation (lex-order).

Theorem. Let `S` be a finite set of points in the plane.

Any angle-optimal triangulation of `S` is a Delauney Triangulation of `S`.
Any Delauney Triangulation of `S` maximizes the minimal angles of the triangles in any triangulation of `S`. If no four points of S lie on a circle, then the Delauney Triangulation of `S` is angle optimal.

Computing a Voronoi Diagram

It can be shown that sorting can be reduced to computing Voronoi diagrams. So there is a `Ω(n cdot log n)` lower bound to the time needed to compute either Voronoi Diagrams or Delauney Triangulations.
One of the best algorithms for computing Voronoi Diagrams is that due to Fortune. It is based on a notion of a sweep line technique and intersections of cones above each point in `S`. It is a `O(n cdot log n)` algorithm.
A simpler algorithm which we will now describe is based on an incremental approach. We assume in the below that we are storing vertices, edges, cells using a winged-edge representation so it is easy to find the faces associated with an edge as well as find the edges of any face. (If you like, this could also be done with a half-edge or quad-edge representation).
To keep things simple we will sometimes allow infinite edges. For such edges, we use a "dummy vertex" whose value is floating point infinity. If both endpoints are at infinity, we also store a finte point on the edge and a direction vector (so we can get the line); if only one end point is at infinity we store the other end point and a direction vector as well as the dummy vertex at infinity.
The Voronoi diagram `D` for two point consists of the edge with endpoints at infinity of the line that bisects these points.
If `S` had three points, we could find the center of the circle they share and shoot out rays between this center bisecting points on the circle to get the Voronoi diagram.
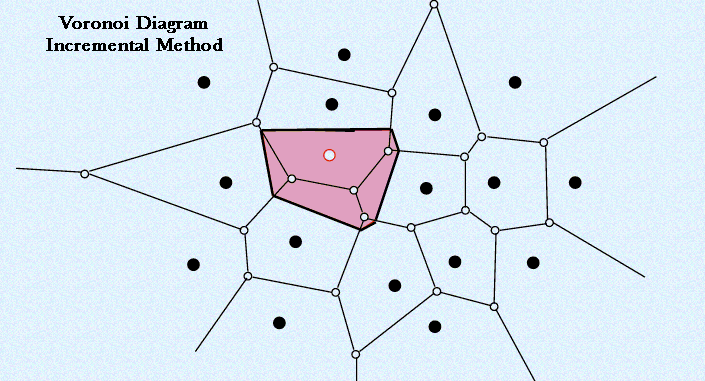
If we have constructed the Voronoi diagram of `k` points and we wish to add another point `vec p`, we first determine which old cell `vec p` belongs to. We will need to modify some of the cells adjacent to this cell and this cell to create the new diagram.
Let `\vec p'` be the point in `S` amongst these `k` first points that belongs to this cell.
Compute the line which bisects `vec p` and `\vec p'` and see which are the two nearest cells this intersects.
For each of these cells compute the bisecting line from `vec p` and the points from `S` they contain.
These bisecting lines can intersect at most one new cell each which we have not seen. For these new cells repeat the process.
This process terminates with the construction of the new cell for `vec p` .
See the diagram above (this come from http://www.personal.kent.edu/~rmuhamma/Compgeometry/MyCG/Voronoi/Incremental2/incremental2.htm).
Given the Voronoi diagram we can then use it to build the Delauney triangulation in a straightforward way making use of the fact that we have a winged-edge representation.

Voronoi Diagrams, Delauney Triangulation

Outline