Introduction

Last week, we went over the Voronoi diagram algorithm in more detail
Then we began talking about curvature and curvature on a surface.
We discussed how curvature is connected to the notion of what it means for a curve to be fair.
We described how a set of points can be approximated by a fair curve.
We also went into how in the recursive subdivision algorithm, the use of chordal distance is a fast proxy for measuring curvature.
Finally, we looked at the Frenet Frame and parallel transport.
Today, we begin by defining what a geodesic is and then go in to some algorithms.

Definition

Geodesics are often given one of a couple different "plain" language definitions:

The Kinematic Definition. A geodesic is a curve traversed by a particle whose acceleration vector at a point lies in the plane spanned by the velocity vector and the normal to the surface at the point. There is no side-to-side acceleration. Any acceleration is used to keep the particle in the surface or to speed it up or slow it down in the direction of the path.

The Static Force Definition. On a convex surface, a curve is called a geodesic if a thread stretched along the path it traces out on the surface is in static equilibrium with respect to any sideways tension on it.

Mathematical Definition

Let `vec phi:[c,d] \times [e,f] \rightarrow \vec S` be a surface.
To get a curve on this surface we can define `gamma(t) = vec phi(vec \alpha(t))` where `vec alpha:[a,b] \rightarrow [c,d]\times [e,f]`.
Let J denote the Jacobian of vector value function (matrix of first partial derivatives).We can compute the first and second derivative of this using the chain rule:
`gamma'(t) = \vec \alpha'(t) J\vec phi(\alpha(t))`
`gamma''(t) = \vec \alpha''J\vec \phi^T + \vec \alpha'(J\vec\phi)'^T`
Mathematically, we define a geodesic to be a curve satisfying the equations:
`\vec gamma''(t)\cdot \frac{del \vec phi}{del u}(vec \alpha(t)) = 0`,
`\vec gamma''(t)\cdot \frac{del \vec phi}{del v}(vec \alpha(t)) = 0`,
The definition of the previous slide turn out to be slight weakenings of this.
Let `\vec b(t) = \vec n(\vec \gamma(t)) \times \gamma'(t)` where `\vec n = \frac{del \vec phi}{del u} \times \frac{del \vec phi}{del v}` is the normal to the tangent plane.
Then the conditions of the last slide give:
`\vec gamma''(t)\cdot \vec b(t) = 0`.
The second condition is slightly weaker in that it doesn't guarantee, `\vec gamma''(t)` is normal to the surface.
As an example of a geodesic, take a sphere and any two points `vec x`,`vec y` on it. Cut this sphere the plane P through the origin of the sphere and these two points. Look at the circle on gets on the sphere, this is a geodesic. Note `vec \gamma''(t)` at `vec x` or `vec y` or at any point along this curve points at the center of the sphere. This in turn will be a normal to the tangent plane. As `vec b` is orthogonal to this normal the kinematic geodesic condition is satisfied.

Quiz

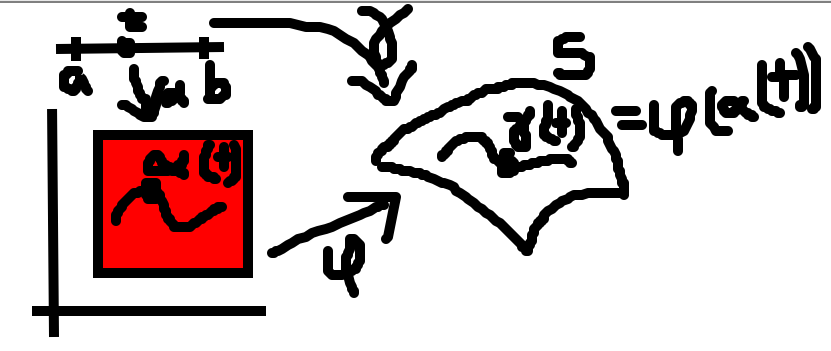
Which of the following statements is true?

We defined Gaussian curvature with respect to geodesic curvature.
Finding the nearest curve `vec q` comes to a point `vec p` amounts to solving the equation: `(\vec p - \vec q(u))\cdot vec q'(u) = 0`.
A parallel transport frame and a Frenet frame are the same thing.

Applications of Geodesics

One use of geodesics is to find the shortest path between two points on a surface.

For instance, maybe we want to model the path taken by a river down a jagged mountain. We could start by finding a geodesics then maybe adding a perpendicular meander.

Another use for geodesics is if we have a base curve and we want to create an offset of it moved over by a certain amount (an offset curve). This can be gotten by moving the curve over along a geodesic. Alternatively, you can think of this as moving the curve via parallel transport.

Discrete Geodesics

We will now look at how to solve this problem when our surfaces and polygonal. That is, described by polygon faces.

Definition. A piecewise linear (pwl) curve `p` in `mathbb{R}^n` is a sequence `(\vec p_0, \ldots, vec p_k)` of points. The length of `p` is the sum of the length `||p_(i+1) - p_(i)||`. The curve is closed if its first and last points are the same, and is simple if all other points are distinct.

Theorem. Let `vec S` be a connected compact polygonal surface. (1) any two points of `vec S` can be connected by a shortest pwl curve. (2) Every shortest pwl curve between two points in `vec S` is simple. (3) There is a `\delta > 0` so that for any two points `vec p` and `vec q` in `vec S` with `|| \vec p - \vec q|| < \delta`, there is a unique shortest pwl curve from `vec p` to `vec q`.

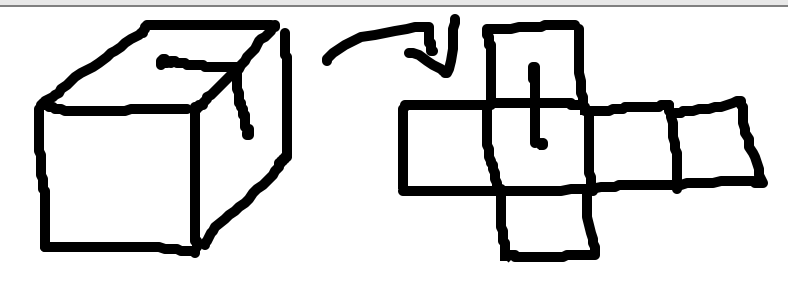
The idea of the proof is that by cutting the polygonal surface along edges, we can flatten it out so that it lies entirely in the plane. Then the theorem follows from shortest distance between points in the plane.

The Discrete Geodesic Problem

Our problem is: Given two points `vec p` and `vec q` on a polygonal surface, find a shortest pwl curve in `vec S` from `vec p` to `vec q`

WLOG, we will assume our surface is triangulated. For simplicity, we also assume it does not have a boundary.
Two faces are edge adjacent if they meet in a common edge.
We will write `(F_1, \ldots, F_k)` for a sequence of edge adjacent faces. Some faces might be repeated in this sequence.
A face sequence induces an edge sequence `(e_1, \ldots. e_(k-1))` of the shared edges.
The unfolding of the sequence `F_1` is just itself, otherwise the unfolding of `(F_1, \ldots F_k)` given the unfolding of `(F_1, \ldots F_(k-1))` consists in rotation the unfolding of `(F_1, \ldots F_(k-1))` into the plane of `F_k`.
It turns out a discrete geodesic on our surface is a curve that alternates between vertices and edge sequences such that the unfolded path along any edge sequence is a straight line segment. If the curve passes through any surface vertex, then the angle the curve makes at the vertex is greater than or equal to `\pi`.
If a discrete geodesic between two points is actually the shortest curve between those points, then no edge can appear in more than one edge sequence and each edge sequence must be simple.

Algorithm for Discrete Geodesic Problem

The basic idea of the algorithm is to start with the face containing one of the two points, say `vec p`, we are trying to connect.
Then using each face connected to this face by an edge (there are special case is `vec p` is a vertex or on an edge of our surface), we decide if we want to add it as a possible next face. i.e., we build a tree where paths in this tree are face sequences.
For a new face, we only add it if the shared edge with the previous face has a sub interval such that the triangle using this sub interval and the base point `vec p` is entirely within the unfolding along the given path's face sequence.
If the surface has n faces the geodesic will involve at most n faces so this algorithm will terminate when we find a path our tree of length at most `n` containing the point we are trying to get to.
The book describes how you can further prune this tree to get an `n^2` algorithm.
For non-convex polygonal surfaces you can actually be reduced to the convex case using Voronoi diagrams.

Geodesics

Outline