Outline
- Using First-Order Logic
- Quiz
- First-Order Theorem Proving Algorithms
Introduction
- We have been talking about first-order logic as a means to extend our logic-based agents to factored domains.
- Last week, we said how to figure out the truth of a statement in a model with respect to a variable assignment,
and how by model checking to determine if a first-order formula follows from a knowledge base.
- We will start today by looking at techniques to use first order logic, and look at algorithms for first-order logic theorem
proving.
- We will then consider one important use of such first order logic agents: Planning.
- This is the search problem of coming up with a sequence of actions which reach a desired goal state and at each time
step satisfy the constraints on the problem at hand.
- The particular planning language we use is a first-order logic called PDDL - Planning Domain Definition Language.
- This is an extension of an earlier language called STRIPS (one of the first famous planning languages from 1971).
Using First-Order Logic
- As in the propositional case, our logic-based agent will tell its knowledge base facts.
- For example,
`TELL(KB, K\i\ng(John))`.
`TELL(KB, Person(Richard))`.
`TELL(KB, forall x K\i\ng(x) => Person(x))`.
- In the course of deciding what to do next, the logic-based agent might ask the knowledge-base questions:
`Ask(KB, K\i\ng(John))`
- Such a question is called a query or a goal. The result in the case should be just True.
- We can ask more complicated questions such as:
`Ask(KB, exists x Person(x))`
- Again, from our knowledge base we can see the answer is True since Richard is a Person. In this case, it also useful to know this
witness to the truth of the question. So in addition to Ask questions like above, we also allow questions like:
`AskVars(KB, Person(x))`
- The response to such a query is a substitution (aka binding list) which makes the query statement true, in this case, {x/Richard}.
Example 1st Order Knowledge bases
- Any relational database.
- The Natural Numbers:
- Has one constant `0` and one function symbol `S`. (The Peano Axioms add to these `+`, and `times`).
- We have two predicate symbols: NatNum(x) which obeys the axioms:
`NatNum(0).`
`forall n, NatNum(n) => NatNum(S(n)))`
we also have equality `=` in our language.
- So `0`, `S(0)`, `S(S(0))`... are natural numbers
- To constrain the behavior of `S` we need to add the axioms:
`forall n, 0 ne S(n).`
`forall m,n, m ne n => S(m) ne S(n)`.
- Set theory:
- Has one constant `O/` (empty) and predicate symbols `in` (element of)
- No function symbols
- Knowledge base for set theory consists of formulas like `neg( O/ in O/)`, `exists x neg(x = O/)`, ...
- `=` abbreviates that `x` and `y` have the same elements.
- The book gives an example of reformulating the Wumpus World in the first-order setting.
KBs, First-Order Proofs
- Write `KB |== F` to mean for all structures `M`, such that `M |== KB`
we also have `M |== F`
- Proofs in 1st Order Logic are
very much like proofs in propositional logic except now we have some additional axioms.
- For example, some possible additional axioms might be:
`(forall x) (neg P) => neg((exists x) P)`
(for every pig, it can't fly = not there is a pig that can fly)
`neg(forall x P) =>(exists x) neg P`
(Not for every horse it is blue = there is a horse that is not blue)
`A(t) => (exists x) A(x)`
`A(x)=> (forall y) A(y)`
etc. In the above, `t` is an arbitrary term, and `x` is a variable.
- In many ways, one can treat the behavior of `forall x F(x)` as a big AND over the substitution of values `x` could take in the formula `F`.
- Similarly, one can treat the behavior of `exists x F(x)` as a big OR over the substitution of values `x` could take in the formula `F`.
- As with OR and AND we can have `exists` and `forall` introduction and elimination rules of inference:
Exists Introduction: `frac(A(t))((exists x) A(x))`
Forall Introduction: `frac(A(y))(forall x A(x))`
Forall Elimination: `frac(forall x A(x))(A(t))`
Exists Elimination: `frac((exists x) A(x) qquad A(y) => gamma)(gamma)`
Quiz
Which of the following is true?
- DPLL's early termination test causes it to return a satisfying assignment if at least one literal in each clause is true
according to the current partial assignment.
- A first order term is built up of constants and relations.
- Any first order formula can be made true in some model with some variable assignment.
Soundness and Completeness
- As with the propositional case one can show that for first-order logic,
`Gamma |-- F` then `Gamma |== F` for the proof system extended by axioms as on the last slide for exists and forall. (Soundness)
- Moreover, if we have a good initial set of propositional axioms, Godel (1930) showed that whenever our proof system can prove a statement
`Gamma |== F` then in fact `Gamma |-- F`. (Completeness)
- It is possible to do model checking in the first-order setting if the universe is finite, but the time complexity is just as bad/worse than the propositional setting.
- So let's consider for a moment how we could make a theorem prover for first-order logic.
Theorem Proving in First-Order Logic
The basic idea is we want to reduce the first-order case to the propositional case. To do this:
- Convert each formula in the set of formulas `KB cup {neg alpha}` using some of the operations previously described into prenex normal form:
`forall vec(x) exists vec(y) forall vec(z) ... G(vec(x), vec(y), vec(z), ...)`
where `G` does not involve quantifiers and may involve `neg, vee, wedge`. The reason why we are working with sets rather than the single formula `KB wedge neg alpha` is to allow for the case KB is an infinite set of formulas.
- Introduce new function symbols for `forall exists` blocks. For example,
`forall x_1 forall x_2, exists y_1, exists y_2, exists y_3 G(x_1, x_2, y_1, y_2, y_3) mbox(transforms to)
forall x_1 forall x_2,G(x_1, x_2, f_1(x_1, x_2), f_2(x_1, x_2), f_3(x_1, x_2))`
This process is called Skolemization. Given a formula `A` we denote its Skolemization as `A^S`. For a set of formula `Gamma` applying Skolemization to each formula yields a set `Gamma^S`. One can show `Gamma |== B` iff `Gamma^S |== B`, so if `KB cup { not alpha}` has refutation then so does `(KB cup {not alpha})^S`.
- If we have all variables bound, and only universal quantifiers, we can ditch the quantifiers and have an open formula with our variables all free.
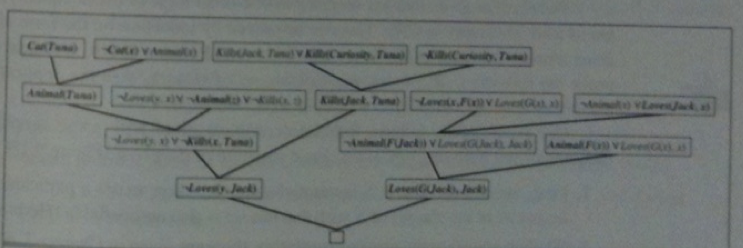
- Once we get open formulas without any quantifiers, convert to CNF and try to use resolution algorithm.
Some remarks on the above:
-
How do we handles formulas with just existentials quantifiers and no universal? Answer: we view these as functions from no arguments to a value. I.e., we replace these with fresh constants.
- How are the new function symbols related to the existing terms in the language before adding the function symbols? In general, a new function symbol `f` is connected to existing function and predicate symbols in the language but won't necessarily be expressible as a term in the original language. For example, Skolemizing an induction axiom:
`A(0, vec a) wedge forall x(A(x, vec a) => A(S(x), vec a)) => A(t(vec a), vec a)`
might yield a function of the predicate `A`, which when given a `t(vec a)` such that `A(0) and neg A(t(vec a))` holds, searches for a value `v` as a function of `vec a`
such that `A(v, vec a)` holds but `A(S(v), vec a)` does not. This search operation might not be expressible as a single term in the original language.
- To do resolution we might now also need to come up with substitution lists between two atomic formulas in `G`, say `F(vec(t))`, `F(vec(s))`,
for the terms `t_1, ..., t_n` and `s_1`, ..., `s_n` so that they are the same formula. This is so that after doing the substitution, we can resolve the two formulas. Unification is an algorithm for doing this.
Unification Algorithm
If x is a list let head(x) denote the first element of the list, x[0], and tail(x) denote x[1:].
The code below relies on Unify-var which is on the next slide.
Unify(x, y, S)
x - a variable, constant, term or list
y - a variable, constant, term, or list
S - a substitution so far
if(S == fail) return fail
if (x(S) == y(S)) return S
else if ( var? (x))
return Unify-var(x, y, S)
else if ( var? (y))
return Unify-var(y, x, S)
else if ( term? (x) and term? (y))
return (Unify(args (x), args(y), Unify( op(x), op(y), S))
else if (list? (x) and list? (y) )
return (Unify(tail(x), tail(y), Unify(head(x), head(y), S)))
else
return fail
As an example of what I mean by op and args, consider x:=((z*z) +35). Here op is the top operation. So op(x) := a + b as + is the outer most function symbol. Here a,b are new variables that don't appear elsewhere. args(x) := (z*z, 35),
so contains two terms: the left and right symbol of +.
Unify-var
Here Unify-var is defined as:
Unify-var(var, y, S)
var - a variable
y - an expression
S - a substitution
if(var |-> val) exists in S
return Unify(val, y, S)
else if (y |-> val) exists in S
return Unify(var, val, S)
else if (occur-ck? (var, y)) return fail;
else
return ( append((var |-> y), S))
Suppose x is f(var), then var occurs in f(var) in the above and occur-ck of (var, x) is true!
(note: prolog doesn't do occur-ck's)
Prolog Example
Prolog uses unification. Consider the Prolog program:
num(0).
num(s(X)) :- num(X).
From the prolog prompt we can then do a query like:
|?- num(Y).
It will unify Y with 0 initially and say
Y = 0
To indicate that num(Y) can be made true if we set Y = 0. If we type `n`, we
are indicating we don't want that solution and it will try to resatisfying the statement with
a different substitution. i.e., it is as if we did the query num(Y), not(Y = 0). To this
Prolog, will now make use of the second rule and return:
Y = s(0)
If Prolog did occurs checks then the following kind of query would fail:
|?- num(s (s (X)))
Example of Unify's Execution
As an example of unify in action, consider:
x' = g(h(x, y), z)
y' = g(w, t(v))
Initially, S is (). Since x' and y' are both terms, we return
Unify((h(x, y), z), (w, t(v)), Unify(g(a, b), g(a, b), ()))
Notice that a, b are new variable names.
The second Unify will return S = (), since both g(a, b) are the same thing.
So now we try to unify two lists (h(x, y), z), (w, t(v)).
So we will do Unify( (z), (t(v)), Unify (h(x, y), w, S)). S is still ().
Now we call Unify-var (w, h(x,y), S).
This statement will return (w |-> h(x, y)).
We now need to unify (z) and (t(v)) with respect to the substitution (w |-> h(x,y)). When we get the final recursive answer, we will have
( (z |-> t(v)), (w |-> h(x,y)) )
Equality
- So many knowledge bases make use of an equality predicate, `=`, that people have studied this predicate and how to handle it in detail.
- One simple approach that people had before people tried to do theorem proving was to just add equality axioms to the knowledge base:
`(forall x) x = x`
`(forall x, y) x = y => y = x`
For any predicate symbol `P`, and substitution slot in this symbol:
`(forall x, y) (x=y ^^ P(..., x, ...)) => P(..., y, ...)`
For any function symbol `f` and substitution slot in this symbol:
`(forall x, y) x=y => f(..., x, ...) = f(..., y, ...).`
- The above approach can entail adding lots of axioms to our knowledge base.
- For theorem proving, it is often more convenient to add fixed and simple rules of inference which have an equivalent effect. For resolution systems,
one rule that works is:
For any terms `r, s, t` where `t` appears somewhere in literal `M_i`, and where `r` and `t` can be unified via `theta`:
`(L_1 vv ...vv L_k vv r=s, qquad M_1 vv ...vv M_n)/(SUB(SUBST(theta, r), SUBST(theta, s), SUBST(theta, L_1 vv ...vv L_k vv M_1 vv ...vv M_n)).`
- The above inference is called paramodulation, the special case without `L_i`'s is called demodulation.
- An example use of this inference is if `theta = {x mapsto A, y mapsto B}`, then:
`(R(y) vv F(A,y)=y, qquad P(F(x,B),x) vv Q(x))/(R(B) vv P(B,A) vv Q(A))`