Introduction

On Monday we began talking about local search problems.
For these problems, the sequence of actions to a solution is not needed. For example, a solution to the 8-queens problem is eight non-attacking queens on a chess board -- we don't care so much how their positions were found.
A local search algorithm operates using a single current node and generally moves to neighbors of that node. We don't keep track of the path history.
We said local search is often used for optimization problems to find the best state with respect to some objective function.
We then discussed the hill climbing algorithm. This algorithm, from a given node, moves to the neighboring node that would result in the greatest upward movement with respect to an objective function.
We gave an example how for the eight queens problem this algorithm makes rapid progress towards finding boards with as few as possible pairs of attacking queens. Unfortunately, it might get stuck in a local maxima.
Let's begin today by looking at some variations on basic hill climbing that might help prevent this.

Variants of Hill-Climbing

One way to avoid local minima, and also to hopefully solve the plateaux problem, is to allow moves that move to the same value as the current state. i.e., a sideways move.
This could lead to an infinite loop, depending on the plateaux, so typically one puts limit on the total number of sideways moves.
With a limit of a 100 consecutive sideways moves, the chance of solving the 8-queens puzzle given a random starting configuration goes from 14% to 94%.
The average solution though takes much longer now 21 moves on success, 64 on failure.
Another variant of hill-climbing is stochastic hill climbing: Choose an uphill move at random from the uphill moves with probability proportional to the steepness of the move. This typically converges to a solution more slowly than deterministic hill-climbing, but tends to find better solutions.
One can make hill-climbing complete by allowing restarts. In random-hill climbing with restarts one runs the hill climbing algorithm from a randomly chosen initial state, sees if one gets a solution, and if not, picks a new random initial state and try again.
If each hill-climbing search has a probability `p` of find a solution than the expected number of restarts is `1/p`.
For the 8-queen problem with no sideways moves `p approx 0.14` and roughly 7 restarts on average are needed to find the goal.
This technique can be used to solve instances of the `n`-queens problems into the millions in under a minute.

Simulated Annealing

Hill-climbing doesn't allow for downwards moves.
We next consider an algorithm that does, simulated annealing.
In metallurgy, annealing is the process used to harden glass or metal by heating a substance to a high temperature and then gradually cooling it. This allows the material to reach a lower crystalline energy state.
In this context we are looking at a minimization problem rather than a maximization problem: We imagine our cost is the energy of the system and we are trying to get the system into as low an energy state as possible.
For example, one could imagine the problem of getting a ping pong ball into the deepest crevasse in a bumpy surface.
The way annealing tries to do this is to shake the surface a whole bunch initially, hoping the ball will go generally downloads and not "bump up" too often. Then one gradually slows down the shaking. Keeping some shaking allows us to climb out of local minima, but we gradually reduce the shaking as we get closer and closer to what we think is a minima.
Simulated annealing (Khachaturyan et al 1979 adapted from Metropolis et al 1953) is a computer simulation of this idea. It has been used in VLSI layout since the 1980s.

Simulated Annealing Algorithm

function SIMULATED-ANNEALING(problem, schedule) returns a solution state
    inputs: problem, a problem
            schedule, a mapping from time "temperature"
    current := MAKE-NODE(problem.INITIAL_STATE)
    for t = 1 to infty do
        T := schedule(t) //typically as t gets larger schedule(t) is smaller
        if(T == 0) return current //when Temperature is 0 return state
        next := a randomly selected successor of current
        DeltaE := next.value - current.value //estimated change in energy
        if(DeltaE < 0) current := next 
        else current := next with probability e^(-DeltaE/T)

In-Class Exercise

7	8	9
4	5	6
@ 1	2	3

Suppose we wanted to do stochastic hill climbing on the above table of utilities. The agent starts in the square with the @ in it. The goal square would be a square of locally maximal utility. We want our choice of action to have probability proportional to its utilities, so that each possible action from a given square to an adjacent square has non-zero probability. Suggest an algorithm to do this. Then run your algorithm by hand and say what it does at each step until you get to the 9 in the upper right corner.

Post your solutions to the Sep 20 In-Class Exercise Thread.

Local Beam Search

Rather than keep track of only one state at a time, one could imagine keeping track of `k` states.
This is what local beam search does (Reddy 1977). It begins with `k` randomly generated states.
At each step the successors of all these states are generated.
If any is the goal, it stops.
Otherwise, the `k` best successors are chosen for the next round.
Notice this is different from doing `k` random restarts as the `k` best states in a given round might not come from the successors of all `k` different current states, but instead may come from only some of them.
As with hill-climbing, beam search can be made stochastic.
The `k` states can be viewed as a pool of candidates and their successors as offspring.

Local Search via Genetic Algorithms

A genetic algorithm is a stochastic beam search in which successor states are generated by combining two parent states rather than by modifying a single state.
Again, an analogy can be made with natural selection, but, whereas, in the stochastic local beam search case offspring are generated by asexual reproduction, in the genetic algorithm case they are generated by sexual reproduction.
GAs begin with a set of `k` randomly generated states called the population.
Each state (individual) is represented as a string over a finite alphabet. For example in the 8-queens, the strings might consist of the position in each column of a queen.
The initial states are ranked according to some fitness function which should be higher for better states. For 8-queens, one might use the number of non-attacking queens.
One selects individuals at random according to fitness to "breed".
A cross-over point is chosen randomly from the positions in the string to generate new strings. A mutation might then be applied.
Finally, this whole process is repeated on the new strings or until a goal or closeness to a goal is achieved.
Genetic algorithms of various types have been explored as far back as Alan Turing in 1950.

Adversarial search

So far we have only been considering single agent environments.
We now switch to looking at multi-agent environments where each agent needs to consider the actions of other agents and how they affects its own welfare.
In particular, we are going to look at competitive environments, which are environments in which agents' goals are in conflict.
Such environments, give rise to adversarial search problems, which are often called games.
We will consider games that involve turn taking, have two players, and are zero sum with perfect information.
Here perfect information means the game is deterministic and the environment visible to all playing; zero sum means if Player 1 gets payoff (+a), then player 2 gets payoff (-a). It is possible for both players to get pay-off 0.

Games defined More Formally

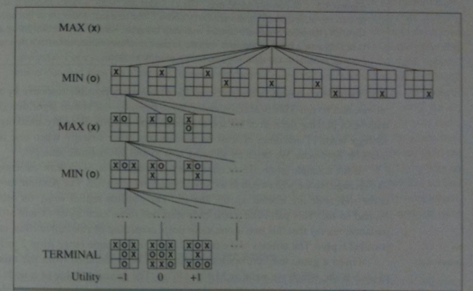
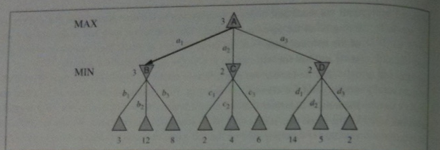
We consider games with two players MAX and MIN. A game consists of:

`S_0` the initial state which specifies how the game is set up at the start.
PLAYER(s): Defines which player has a move in a state `s`.
ACTIONS(s): Returns the set of legal moves in a state
RESULT(s, a): The transition model which defines the results of a move.
TERMINAL-TEST(s): A terminal test that determines when the game is over. States where this evaluates to true are called terminal states.
UTILITY(s, p): A utility function (aka an objective function) defines the final numeric value for a game that ends in terminal `s` for a player `p`. (Use to find out who won.)

Games Trees

The initial state, ACTIONS function, and RESULT function define the game tree for the game -- a tree where nodes are game states and the edges are moves.
Below is an example game tree for Tic-Tac-Toe:
From the initial state MAX has nine possible moves. MAX and MIN take turns, MAX placing X's, MIN placing O's, until we reach leaf nodes corresponding to terminal states.
The number on each leaf indicates the utility value of that terminal. High values are assumed to be good for MAX and bad for MIN.
The tic-tac-toe game is relatively small in that it has fewer than 9! = 362,880 terminal nodes.
Chess on the other hand has `10^(40)` or so nodes, so the game tree cannot be easily created in toto.
A search tree is a sub-tree of the full game tree, that contains enough nodes to allow a player to determine what move to make.

Optimal Strategies

In a normal search problem, the optimal solution is a sequence of actions leading to a goal state -- a terminal state that is a win.
In adversarial search, MAX has to worry about MIN's next move and vice-versa.
MAX, the player who moves first, wants to come up with a strategy for what to do contingent upon MIN playing his best.
An optimal strategy is a sequence of contingent decisions that will lead to outcomes at least as good as any other strategy when one is playing an infallible opponent.
In order to try to figure out an optimal strategy is useful to look at the game tree.

Minimax

To find the optimal strategy for a player, one can compute the minimax value, MINIMAX(n), of each node `n` in the game tree.
This value is the utility of being in the given state, assuming that both players play optimally from there to the end of the game.
`MINIMAX(s) := { ( UTILITY(s), if TERMINAL-TEST(s)), (max_(a in ACTION(s))MINIMAX(RESULT(s, a)),if PLAYER(s) = MAX), (min_(a in ACTION(s))MINIMAX(RESULT(s, a)),if PLAYER(s) = MIN):}`

Minimax Example

Consider the above two move game. In this area, each move is often called a ply.
The utility of each terminal node is listed under it. This would be the minimax value for that node.
At node B, it is MIN's turn, and there are three possible moves: `b_1`, `b_2`, and `b_3`. Of these, `b_1` has the smallest minimax value, so if MIN is playing optimally, MIN will choose `b_1` and so the minimax value of node B is 3.
In a similar fashion, we can compute the minimax values of node C as 2 and node D as 2.
If we move up to node A. Here it is MAX's turn. As MAX wants to get the highest payout possible, MAX will choose a_1 which leads to node B, as node B has the highest minimax value amongst B, C, D.
Thus, the minimax value of node A is 3.
Since A is the root of the current tree, the branch from A, namely `a_1`, which has the minimax value for A, tells MAX what to do next. So it is called the minimax decision for the node.

Local Search Algorithms

Outline