HW1 Solutions Page

Return to homework page.

I am posting solutions to problems 1, 2, and 4. The solution to problems 3 depends on the particular Wizard you chose.

1. (a)

Base Step: A complete 3-ary tree of height 0 is just a tree consisting of the root node. So such a tree has just 1 node. As (3⁰⁺¹-1)/2 = (3-1)/2 = 1, the base case holds.

Induction Step: Assume that any complete 3-ary tree of of height n has (3ⁿ⁺¹-1)/2 nodes. Consider now a complete 3-ary tree of height n+1. The root node of such a tree has three subtrees attached to it, each of these being complete 3-ary tree of height n. By the induction hypothesis, each of these trees has (3ⁿ⁺¹-1)/2 nodes. So the total number of nodes in the whole tree is 3×(3ⁿ⁺¹-1)/2 +1, the +1 is because we need to include the root node. This equals (3ⁿ⁺²-3)/2 + 2/2 which in turn equals (3ⁿ⁺²-1)/2 establishing the induction step and the result.

1. (b)

Base Step: We need to show there is no one-to-one map from a set A of size 1 into a set B of size 0. As the only set of size 0 is the empty set, this trivially holds because there is no place to map A's only element to.

Induction Step: Assume that there do not exists 1-1 maps from a set of n+1 elements into a set of n elements. Consider a function f: A --> B where |A|=n+2 and |B|=n+1. Pick some a∈ A and consider f as restricted to a map A-a --> B-{f(a)}. If f is 1-1, then this restricted function will also be 1-1. On the other hand, the restricted function maps a set of size n+1 into a set of size n. So by the induction hypothesis, it can't be 1-1. Therefore, f can't be 1-1, proving the induction step.

2. To show the binary relation on functions from the positive integers to the positive integers, f(n)=Θ(g(n)), is an equivalence relation, we need to show that it is reflexive, symmetric, and transitive.

Reflexivity: Let f(n) be an arbitrary function from the positive integers to the positive integers. For f(n)=Θ(f(n)) to hold, by definition we must have f(n)=O(f(n)) and O(f(n))=f(n). Both of these conditions are the same. For f(n)=O(f(n)) to hold, by definition we need to prove there is an positive integer N and a constant c> 0 such that for all n≥ N, f(n) ≤ c×f(n). But trivially for all n≥ 1, f(n) ≤ 1× f(n), so this condition holds.

Symmetry: Let f(n) and g(n) be arbitrary functions from the positive integers to the positive integers. We want to show that if f(n)=Θ(g(n)) holds then g(n)=Θ(f(n)) holds. Notice that f(n)=Θ(g(n)) means that the two conditions f(n) = O(g(n)) and g(n) = O(f(n)) hold. On the other hand g(n)=Θ(f(n)) means that the two conditions g(n) = O(f(n)) and f(n) = O(g(n)) hold. These are exactly the same two conditions just written in a different order, so if f(n)=Θ(g(n)) holds then we will have that g(n)=Θ(f(n)) holds.

Transitivity: Let f(n), g(n), and h(n) be arbitrary functions from the positive integers to the positive integers. We want to show that if both f(n)=Θ(g(n)) and g(n)=Θ(h(n)) hold, then f(n)=Θ(h(n)) holds. So if both f(n)=Θ(g(n)) and g(n)=Θ(h(n)) hold, we need to show that f(n)=O(h(n)) and h(n)=O(f(n)) hold. Assuming f(n)=Θ(g(n)) and g(n)=Θ(h(n)), we then have that f(n) = O(g(n)) and g(n)=O(h(n)). Therefore, there are constants b,c> 0, and integers N, M > 0 such that f(n) ≤ b× g(n) for all n≥N and such that g(m) ≤ c× h(m) for all m≥ M. Set K= max(N, M). Using these two inequalities, we then have that f(n) ≤ b×c×h(n) for all n ≥ K. i.e., we have shown f(n)=O(h(n)). On the other hand assuming both f(n)=Θ(g(n)) and g(n)=Θ(h(n)) we also have that g(n)=O(f(n)) and h(n)=O(g(n)). Therefore, there are constants b,c> 0, and integers N, M > 0 such that g(n) ≤ b× f(n) for all n≥N and such that h(m) ≤ c× g(m) for all m≥ M. Set K= max(N, M). Using these two inequalities, we then have that h(n) ≤ b×c×f(n) for all n ≥ K. i.e., we have shown h(n)=O(f(n)). Since from f(n)=Θ(g(n)) and g(n)=Θ(h(n)), we have shown both f(n)=O(h(n)) and h(n)=O(f(n)) follow, we have thus established under these assumptions that f(n)=Θ(h(n)).

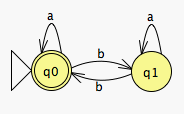
4. Here is an image of a JFLAP DFA for the language over {a,b} consisting of strings with an even number of b's.