Outline

• Regular Languages can be expressed by Regular Expressions
• Quiz
• Regular Grammars
• Classifying Regular Languages

Proof that regular implies the language of some regular expression

• We will split the proof into two parts:
  • We first define a new kind of finite automata called a generalized nondeterministic finite automata (GNFA) and show how to convert any DFA into a GNFA of a special form.
  • Then we show how to convert this special form GNFA into a regular expression.
• To begin we define a GNFA to be an NFA modified to allow transition arrows to have any regular expression as labels. For example `a^star b` would be a legal transition label.
• To make this more formal, we define the transition function of a GNFA to be a map `delta:(Q - {q_(mbox(accept))}) times (Q - {q_(mbox(start))}) rightarrow mathcal(R)` where `mathcal(R)` is the set of all regular expressions. (As we will say on the next slide we assume there is a single accept state.)

Converting DFAs to GNFA

• We will be interested in GNFAs that have the following special form:
  • The start state has transition arrows to every other state but no arrows coming in from other states.
  • There is a single accept state, and it has arrows coming in from every other state but no arrows going to any other state.
  • Except for the start and accepts state, one arrow goes from every state to every other state and also from each state to itself.
• To convert a DFA into a GNFA, we add a new start state with and `epsilon` arrow to the old start state and a new accept state with `epsilon` arrows from the old accept states.
• If any arrows have multiple labels (or if we have two or more arrows between the same two states) we replace each with a single label whose label is the union labels of the these arrows.
• Finally, we add arrows with labels `emptyset` between states which had no labels so as to satisfy the remaining conditions of our special form.

Converting GNFAs to Regular expressions

• Our conversion above gives a GNFA with `k geq 2` states.
• If `k > 2`, we will construct an equivalent GNFA with `k-1` states.
• To do this we pick some state `q_(mbox(rip))` other than the start or accept state, and we will rip it out of the machine.
• To compensate for the loss of this state, for any pair of states `q_i`, `q_j`. in this new machine we replace `delta(q_i, q_j)` with: `delta'(q_i, q_j) =(R_1R_2^star R_3)\cup(R_4)` where `delta(q_i, q_(mbox(rip))) = R_1`; `delta(q_(mbox(rip)), q_(mbox(rip))) = R_2`; `delta(q_(mbox(rip)), q_j) = R_3`; `delta(q_i, q_j) = R_4`.
• This machine will be equivalent to the old machine.
• Further, by repeatedly ripping out states in this fashion we can get down to the 2-state machine with just a regular expression on the single transition between these two states.
• This regular expression will be equivalent to the original NFA.

The proof of equivalence of finite automata and regular expressions is due to McNaughton and Yamada (1960).

Corollary

The regular languages are closed under union, `star`, and concatenation.

Proof. The regular languages are precisely those recognized by DFAs. We have shown in turn that the languages recognized by DFAs are precisely those recognized by NFAs, and these in turn are precisely the languages recognized by regular expression. As the languages of regular expressions are trivially closed under these operations, we get the regular languages are closed under these operations.

Quiz Sec 1

Which of the following is true?

1. Reversing the accepting and rejecting states of a NFA `M` yields a NFA recognizing `bar(L(M))`.
2. Given two `n` state DFAs, `M_1`, `M_2` there is a DFA recognizing `L(M_1) cup L(M_2)` that has at most `n^2` states.
3. It is possible for two states in a finite automata to be indistinguishable, yet one is accepting and the other rejecting.

Quiz Sec 3

Which of the following is true?

1. Our minimization procedure from class for a DFA `M` runs in linear time in the number of states of `M`.
2. Without change a 5-tuple which matches our definition of being a DFA is a 5-tuple matching our definition of being an NFA.
3. If DFA `M=(Q,Sigma, delta, q_0, F)` recognizes language `L`, then `M'=(Q, Sigma, delta, q_0, bar{F})` recognizes `bar(L)` because for DFAs `delta^\star` is a function to `Q` not `P(Q)`.

Grammars

• We now consider a different way to look at the regular languages based on grammars.
• A grammar is defined as a 4-tuple `G=(V, T, P, S)` where `V` is a finite set of variables, `T` is a finite set of terminal symbols, `S in V` is called the start variable, and `P` is a finite set of productions of the form `v rightarrow w` where `v` is in `(V cup T)^+` and `w` is in `(V cup T)^star`.
• For example, let `G=({<mbox(sentence)>, <mbox(noun)>, <mbox(verb)>}, {mbox(dog), mbox(cat), mbox(walks), mbox(eats)}, P, <sentence>)` where `P` is
  `<mbox(sentence)> rightarrow <mbox(noun)> \ <mbox(verb)> \ <mbox(sentence)>`
  `<mbox(sentence)> rightarrow <mbox(noun)> <mbox(verb)>`
  `<mbox(noun)> rightarrow mbox(dog) | mbox(cat)` /* we are using `|` to abbreviate two line `<mbox(noun)> rightarrow mbox(dog)` and `<mbox(noun)> rightarrow mbox(cat)` */
  `<mbox(verb)> rightarrow mbox(walks) | mbox(eats)`
  `<mbox(noun)> <mbox(verb)> rightarrow <mbox(sentence)>`
• Beginning with the start variable, a grammar can yield or generate a string over the alphabet of terminals via a finite sequence of substitutions:
  `<mbox(sentence)> => <mbox(noun)> <mbox(verb)> => mbox(dog) <mbox(verb)> => mbox(dog) \ mbox(walks)`
  we write `<sentence> =>^star dog \ walks` to indicate from the string <sentence> we can get dog walks via a finite sequence of substitutions.
• We write `L(G)` for the set of strings generated by a grammar.

Regular Grammars

• A grammar `G=(V, T, P, S)` is called right-linear if all its productions are of the form `A -> xB` or `A -> x` for some `A`, `B in V` and `x in T^star`.
• A grammar is called left-linear if all its productions are of the form `A -> Bx` or `A -> x` for some `A, B in V` and `x in T^star`.
• A grammar is called regular if it is either left or right linear.
• For example, `G=({S}, {a,b}, P, S)` where `P` contains `S -> abS | epsilon` is right linear. It generates the strings in `(ab)^star`.
• For example, `G=({S, A}, {a,b}, P, S)` where P contains `S -> Sab |A`, `A -> Aba | ba` is left linear. It generates the strings in `(ba)^+(ab)^star`.
• The set of rules `S ->A`, `A -> aB|epsilon`, `A -> Ab` are all linear (so could belong to a linear grammar). The second rule is right linear, and the third is left linear, so these rules together could not belong to either a right linear or left linear grammar.

Equivalence with Regular Languages

• To prove this we need to show every language generated by a regular grammar is regular and vice-versa.
• In class we will only look at right linear grammars, but a similar argument can be made for left linear grammars. To begin:

  Theorem. Let `G=(V, T, P, S)` be a right linear grammar. Then `L(G)` is a regular language.

  Proof. Let `V={V_0, ldots , V_n}`. Assume `S=V_0`. The alphabet of our NFA will be the set of terminals. The set of states of our NFA will consist of `V_0, ldots, V_n` together with some auxiliary states and the state `F` which will be the unique accepting state. The start state will be `V_0`. The transition function `delta` will be based on the productions of `G`. A production `V_i -> a_1 ldots a_m V_j` will map to the sequence of states and transitions:
  
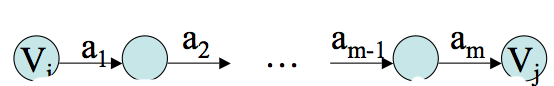
  where the unlabelled states are auxiliary states.
  A production of the form `V_i -> a_1 ldots a_m` is mapped to a set of transitions:
  
  Given this description of the NFA, one can observe that `V_0 =>^star w` if and only if `delta^star(V_0, w) = F` and so if and only if `w` is accepted by the NFA.

Regular implies Regular Grammar

Theorem. If `L` is a regular language, then it is generated by right linear grammar.

Proof. Let `M = (Q, Sigma, delta, q_0, F)` be a DFA for `L`. Assume `Q={q_0, ldots, q_n}` and `Sigma={a_0, ..., a_m}`. Let `G=(V, Sigma, P, S)` be the grammar with `V={q_0, ..., q_n}` and `S= q_0` and where for each transition `delta(q_i, a_j) = q_k` we have the production `q_i -> a_jq_k` and if `q_k` is in `F` we also have the production `q_k -> epsilon`. It is not hard to see that `w` is accepted by `M` iff it is generated by this right linear grammar.

Regular Grammars and the equivalences between their languages and the regular languages is due to Chomsky and Miller. Information and Control. Vol. 1. 1958. pp 91--112.

Classifying Regular Languages

• Besides giving a convenient format for describing a regular language, regular expressions can also be used to measure how hard a regular language is.
• If you think about our proof that NFAs can simulate each of the regular operations, only simulation of Kleene Star involved creating loops in the automata graph. So it natural to estimate "how complex" an automata is by counting nestings of Kleene Star.
• We define the star-height of a regular expression inductively. If `R` is `emptyset`, `epsilon` or an alphabet symbol `mbox(star)(R) := 0`. Given regular expressions `R_1` and `R_2`, `mbox(star)((R_1 cup R_2)) = mbox(star)((R_1R_2)) := \max(mbox(star)(R_1),mbox(star)(R_2))` and `mbox(star)(R_1^\star) := mbox(star)(R_1) + 1`.
• Hence, given a regular expression `R` there is a simple recursive algorithm to compute its star-height. On the other hand it is unclear whether one couldn't find an `R'` with the same language of smaller star-height.

Facts about Star-height

• Eggan (1963) showed that there are languages which require arbitrarily large star-height.
• Kirsten (2005) gives a double exponential-space algorithm for computing the minimal star-height of a language.
• Languages of star-height 0 have an abstract algebra characterization in terms of so-called aperiodic syntactic monoids, Schutzenberg (1965).
• For higher star-height, there are notions like locally testable, and piecewise testable expressions, which have characterizations in terms of pseudo-varieties of monoids (Eilenberg).
• A generalized regular expression is defined the same way as a regular expression but we also allow `cap`. This doesn't effect the class of languages since one can show that the regular language are closed under intersection via a Cartesian product construction.
• It is open whether star-height greater than 1 is needed for generalized regular expressions.