Outline

• CFG Closure Properties
• CFG algorithms
• HW Problem
• Turing Machines

Closure Properties of CFL

CFL are closed under union

Proof idea: Let `G` and `H` with start symbols `S` and `T` respectively, be two CFGs for the CFL's we want to take the union of. Make a new grammar with the same alphabet, with the union of the two grammars productions (after renaming) together with the new rules `S'->S|T` where `S'` is the new start variable.

CFLs are closed under intersection by regular languages

Proof idea: use the Cartesian product construction on a PDA for the CFL together with a DFA for the regular language.

CFLs are not closed under intersection or complementation

Proof: The languages `{a^nb^nc^m | n, m ge 0}` and `{a^mb^nc^n | n, m ge0}` are both context-free. Their intersection is `{a^nb^nc^n | n ge 0}` which is not CFL by the pumping lemma. CFLs are not closed under complementation as using deMorgan rules, intersection can be defined from union and complementation.

Algorithms for CFLs

• We have already given an algorithm (CYK) for checking if a string is in a CFL.
• We have also given algorithms for checking for useless variables in grammars, as well as, for eliminating `epsilon`-rules from grammars.
• Here are a couple of more things we have CFG algorithms for:

There is an algorithm, which given a grammar `G` written down formally as a 4-tuple, can decide whether or not `L(G)` is empty.

To do this, the algorithm check if the start variable is useless. If it is we know the language is empty; otherwise it is not.

There is an algorithm to check given G whether or not L(G) is infinite.

To do this, we first eliminate `epsilon`-rules, unit-productions, and useless symbols from `G`. We then construct a graph where `(A,B)` is an edge for two variables `A`, `B` in the graph iff `A->xBy` for some production in `G`. If there is a cycle in this graph then `C=>^star uCv` for some variable `C` in the original grammar. As there are no useless symbols in this grammar, we must have `C=>^star z`, for some string `z` of terminals. Hence, also, `S=>^star sCt =>^star szt, S=>^star sCt =>^star suCvt =>^star suzvt`, etc. Thus, one can argue there is a cycle in the graph iff `G'`s grammar is infinite.

Homework Problems (Sec 1) and (Sec 3)

Problem 2. Give a CFG for the language consisting of balanced parentheses. Use the algorithm from class to convert this CFG into a PDA. Show formally how this PDA would accept the string `(()())`.

Answer. A CFG for this language is:

Converting this to a PDA according to the method from class gives:

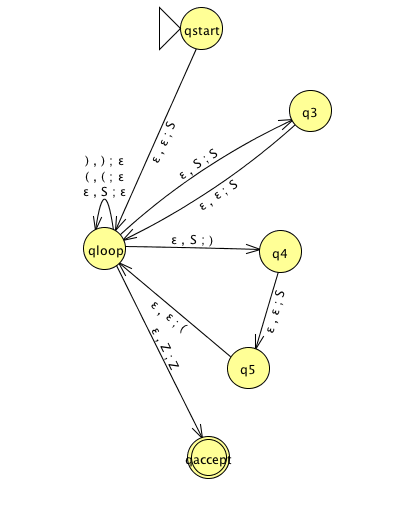
Given the input string `w=(()())` we need to come up with sequence `w_i`, `r_i` and `s_i` that match the definition of acceptance for a PDA. We list these below

`r_0 = q_(\mbox(start))` and `s_0 = Z`
`r_1 = q_(\mbox(loop))` and `s_1 = SZ` and `w_1 = epsilon`, using `(q_(\mbox(loop)), S) in delta(q_(\mbox(start)), epsilon, epsilon)`.
`r_2 = q_(4)` and `s_2 = )Z` and `w_2 = epsilon`, using `(``q_4, '``)``'``)`` in delta(q_(\mbox(loop)), epsilon, S)`.
`r_3 = q_5` and `s_3 = S)Z` and `w_3 = epsilon`, using `(q_5, S) in delta(q_4, epsilon, epsilon)`.
`r_4 = q_(\mbox(loop))` and `s_4 = (S)Z` and `w_4 = epsilon`, using `(q_(\mbox(loop)), '``(``'``)`` in delta(q_5, epsilon, epsilon)`.
`r_5 = q_(\mbox(loop))` and `s_5 = S)Z` and `w_5 = '('`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), '``(``', '``(``')`.
`r_6 = q_(3)` and `s_6 = S)Z` and `w_6 = epsilon`, using `(q_3, S) in delta(q_(\mbox(loop)), epsilon, S)`.
`r_7 = q_(\mbox(loop))` and `s_7 = SS)Z` and `w_7 = epsilon`, using `(q_(\mbox(loop)), S) in delta(q_3, epsilon, epsilon)`.
`r_8 = q_(4)` and `s_8 = )S)Z` and `w_8 = epsilon`, using `(``q_4, '``)``'``)`` in delta(q_(\mbox(loop)), epsilon, S)`.
`r_9 = q_5` and `s_9 = S)S)Z` and `w_9 = epsilon`, using `(q_5, S) in delta(q_4, epsilon, epsilon)`.
`r_(10) = q_(\mbox(loop))` and `s_(10) = (S)S)Z` and `w_(10) = epsilon`, using `(q_(\mbox(loop)), '``(``'``)`` in delta(q_5, epsilon, epsilon)`.
`r_(11) = q_(\mbox(loop))` and `s_(11) = S)S)Z` and `w_(11) = '('`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), '``(``', '``(``')`.
`r_(12) = q_(\mbox(loop))` and `s_(12) = )S)Z` and `w_12 = epsilon`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), epsilon, S)`.
`r_(13) = q_(\mbox(loop))` and `s_(13) = S)Z` and `w_(13) = ')'`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), '``)``', '``)``')`.
`r_(14) = q_(4)` and `s_(14) = ))Z` and `w_(14) = epsilon`, using `(``q_4, '``)``'``)`` in delta(q_(\mbox(loop)), epsilon, S)`.
`r_(15) = q_5` and `s_(15) = S))Z` and `w_(15) = epsilon`, using `(q_5, S) in delta(q_4, epsilon, epsilon)`.
`r_(16) = q_(\mbox(loop))` and `s_(16) = (S))Z` and `w_(16) = epsilon`, using `(q_(\mbox(loop)), '``(``'``)`` in delta(q_5, epsilon, epsilon)`.
`r_(17) = q_(\mbox(loop))` and `s_(17) = S))Z` and `w_(17) = '('`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), '``(``', '``(``')`.
`r_(18) = q_(\mbox(loop))` and `s_(18) = ))Z` and `w_18 = epsilon`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), epsilon, S)`.
`r_(19) = q_(\mbox(loop))` and `s_(19) = )Z` and `w_(19) = ')'`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), '``)``', '``)``')`.
`r_(20) = q_(\mbox(loop))` and `s_(20) = Z` and `w_(20) = ')'`, using `(q_(\mbox(loop)), epsilon) in delta(q_(\mbox(loop)), '``)``', '``)``')`.
`r_(21) = q_(\mbox(accept))` and `s_(21) = Z` and `w_(21) = epsilon`, using `(q_(\mbox(accept)), Z) in delta(q_(\mbox(loop)), epsilon, Z)`.

Problem 4. Consider the language `L` consisting of all strings over `{0,1}` of the form `0^{2n}1^{n}0^{n}1^{2n}` for any `n ge 0`. Show using the pumping lemma this language is not context-free.

Answer. Assume this language was CFL. Let `G` be a CFG generating it. Let `p` be the pumping length given by the pumping lemma. Consider the string `w=0^{2p}1^{p}0^{p}1^{2p}`. As `w in L`, by the pumping lemma, `w` can be written in the form `uvxyz` with `|vxy| < p`, `|vy| > 0` and such that `uv^jxy^jz` is in `L` for `j ge 0`. There are two main cases to consider: either (1) `v` or `y` contains both a `0`s and `1`s or (2) `v` is made up of only `0`s or only `1`s and `y` is made up of only `0` or only `1`'s. In case (1) the string `uv^2xy^2z` with have at least one more alternation between 0's and 1's than the string `w` and all other strings in `L` which should have only 3 alternations `0->^(1)1->^(2)0->^(3)1`, so we get a contradiction, despite the pumping lemma saying it should be in the language it is not in the correct format. For case (2), since `|vxy| < p` and `|w| = 6p` it is either within the first `3p` symbols, or within the last `3p` symbols, or within the middle `2p` symbols. By the pumping lemma the string `uv^0xy^0z` if `vxy` is within the first `3p` or last `3p` symbols then the other half will have too many `0`'s and `1`'s to be in the correct format for a string in the language since `|vy| > 0`. On the other hand, if `vxy` is from the middle `2p` symbols, then `uv^0xy^0z = 0^{2p}1^{k}0^{j}1^{2p}` where either `k` or `j` is strictly less than `p` so again the string does not have the correct format to be in `L`. Hence, for all ways we could split the string according to the pumping lemma we get a contradiction. Therefore, our assumption that the language was CFL must be false.

General Models of Computation

• So far we have looked at machines that either have bounded memory or access to memory limited to stack operations.
• We would like to consider models of computation which correspond to general purpose computers.
• In 1936 ("On Computable Numbers", London Math Society), Alan Turing presented such a general model of a computer, the Turing Machine.
• In this model, the machine has a finite control and an arbitrarily long tape of data consisting of squares able to hold one symbol. The machine also has a read head which can read one square at a time. Initially, this tape is blank except for the n first squares under and to the right of the tape head which have the input. The machine in one step is allowed to read what's under its tape head, write a new symbol, move left or right one square and change its state.
• The machine has special states which cause it to halt. The contents of the tape when these states are entered is the output of the machine.
• The first actual computer developed for code-breaking during World War II was partially based on his model.
• It turns out this model is actually equivalent to what can be done on modern computers.

A Real-Life Turing Machine

[YouTube video of above machine in action]

Example

• Let `B` be the language `{w\#w | w in {0,1}^star }`. This language is not context-free.
• A Turing Machine `M` that could accept this language might operate as follows:
  

   On input `w`:
  (1) Zig-zag across the tape to the corresponding positions on either 
  side of the # symbol to check whether these positions contain the 
  same symbol. If they do not, or if no # is found do into the 
  reject state. If they have the same symbol change the symbol 
  to a new symbol X.
  (2) When all the symbols on the left side of the # have been 
  X'd out, check if there are any more symbols to the right of the #. 
  If yes reject; if not accept.
  

• By accept or reject, I mean we view the halting states as further partitioned into those which are accepting and those which are rejecting and we enter the appropriate kind of halting state.

Formal Definition of Turing Machine

• A Turing Machine (TM)s a 6-tuple `(Q, Sigma, Gamma, delta, q_0, H)` where
  1. `Q` is a finite set of states
  2. `Sigma subseteq Gamma` are respectively the input and tape alphabets. `Gamma` contains a space symbol '`\square`' not in `Sigma`.
  3. `delta:Q times Gamma -> Q times Gamma times {L, R}` is the transition function. (JFLAP allows L,R,S where S is stay put).
  4. `q_0 in Q` is the start state.
  5. `H subseteq Q` is the set of Halting states of the machine
• A TM receives its input `w=w_1w_2 ldots w_n` on the `n` squares of its tape under and to the right of the tape head. The input is not allowed to contain blanks. The tape has arbitrarily many tape square to the right and to the left of the starting tape head location. Except for the input, the rest of the tape squares have the blank symbol. Once `M` starts, it follows the rules prescribed by the transition function. A rule `(q,a)->(q',b, L)` says in state `q` reading an `a` go to state `q'`, write a `b` in the current square then move the tape head left. `(q,a) ->(q',b, R)` would say the same thing except moves the tape head right. Computation continues until the machine enters a halt state.

Diagrams and Examples

• As you can see above, there is a diagrammatic notation for Turing Machines similar to that for PDA and DFAs.
• The states are drawn as circles; two concentric circles indicates a halt state (the book calls these final states).
• Each transition is labeled with a triple `mbox(x;y, D)`; where `x` is supposed to be the symbol being read, `y` is the symbol to write, and `D` is the direction to move.
• For example, the above machine when started on a string over the alphabet `{a,b}` converts it to a string of the same length consisting of only `b`'s, then stops on the rightmost character of the output string.

Configurations, Yields

• To specify the state of a computation at a given time (i.e., a configuration) one needs to specify the tape contents, the head position, and the current state.
• To do this it suffices to consider only the non-blank squares.
• One can use the notation `u q v` to represent this information. Here `u` is a string that represents the contents of the tape to the left of the tape head, `q` is the current state and `v` is a string consisting of what is under the tape head followed by the non-blank symbols to the right of the tape head.
• For example, one might have `0011q71100`. This says the tape contents are `00111100`, the machine is in state `q7`, and it is reading the third 1 in this string.
• We say configuration `C` yields `C'` if the TM can legally go from `C` to `C'` in one step. For instance, `ua q bv` yields `u q' acv` if `delta(q,b) =(q', c, L)`.

Accept, Reject, Recognize, Decide

• The start configuration of `M` on input `w` is the configuration `q_0 w`.
• An accepting configuration is one in which the state of the configuration is `q_mbox(accept)`, where `q_mbox(accept)` is some state in `H`.
• A rejecting configuration is one in which the state of the configuration is `q_mbox(reject)` where `q_mbox(reject)` is some state in `H`.
• A Turing machine `M` accepts `w` if a there is a sequence of configurations `C_1, C_2,ldots , C_k` such that `C_1` is the start configuration of `M` on `w`; for `i` between `1` and `k-1`, `C_i` yields `C_(i+1)` and `C_k` is an accept configuration.
• The collection of strings `M` accepts is denoted `L(M)` and is called the language recognized by `M`.
• A language is Turing-recognizable if some TM recognizes it.
• A language is called decidable if there is some TM that halts on all inputs and that recognizes the language.