Outline

• PDA to CFL
• Quiz
• Pumping Lemma for CFGs
• String Compression with CFGs

PDA to CFL

Let `P` be a PDA. We want to make a CFG `G` that generates the same language.

• For each pair of states `p`, `q` in `P` we will have in `G` a variable `A_(pq)`. This variable will be able to generate all strings that can take `P` in state `p` with the empty stack to state `q` with the empty stack.
• To simplify the problem we will assume `P` has been modified so that:
  • it has a single accept state
  • it empties its stack before accepting
  • each transition either pushes a symbol onto the stack or pops one off of the stack (but not both). (We might add states to make our machine have this property).
• `G` will have rules `A_(pp) -> epsilon` for each state `p` of `P`; `A_(pq) -> aA_(rs)b` for each `p`, `q`, `r`, `s` such that `delta(p,a, epsilon)` contains `(r,t)` and `delta(s,b, t)` contains `(q, epsilon)`, and `A_(pq) -> A_(pr)A_(rq)` for any state `r`.
• The start variable of `G` will be `A_(q_0,q_(mbox(accept)))`.

The proof that languages given by PDAs and the CFLs are the same is due independently to Chomsky (1962), Schutzenberger (1963), and Evey (1963).

Example PDA in JFLAP and of PDA to CFL conversion

• Consider the PDA:
  
• Notice the diagram comes from JFLAP. To make PDAs in JFLAP on the main button panel of JFLAP select "Pushdown Automata".
• This allows the user to create pushdown automata in much the same way as DFAs are made in JFLAP.
• When you choose Step-by-State menu item to run an automata on some inputs you will notice that the starting stack symbol is always "`Z`".
• The automata above recognizes the language `{a^nb^n | n >0}`.
• It has a single accept state and each transition either pushes or pops a symbol, so we can apply the construction.
• This machine empties the stack except for the start of stack symbol.
• The start variable given by the construction of the last slide will be `A_(q_0q_3)`. We'll abbreviate this as `A_(03)`.
• Many of the rules the construction would give are completely useless; nevertheless, one can check it does produce the rules `A_(03) -> epsilon A_(12) epsilon`, `A_(12)->aA_(12)b`, `A_(12)->aA_(11)b`, and `A_(11)->epsilon`.

Another Proof of the PDA to CFL result

• If you try to convert a PDA to a CFG in JFLAP you will notice that the algorithm is not the same as two slides back.
• Instead, JFLAP uses an algorithm based on the following proof:
  

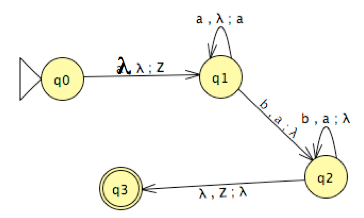
  Alternative Proof can convert from PDA to a CFG. Let `N` be a PDA. Without loss of generality we assume the final state of `N` is entered iff the stack is empty. We also assume that any move of `N` increases or decreases the stack content by a single symbol. We set the variables of the simulating CFG to be of the form `(q_iAq_j)` where `q_i` and `q_j` are states of `N`. Our grammar will have rules that ensure that:
  `(q_iAq_j) =>^\star v`
  iff `N` erases `A` from the stack while reading `v` and going from state `q_i` to `q_j`. If our grammar has this property, and we choose `q_(\mbox(start))zq_(\mbox(final))` as the start symbol, then
  `q_(\mbox(start))zq_(\mbox(final)) =>^star w`
  iff `N` accepts `w`. To complete our proof, we now say the rules of our grammar and leave it to the reader to verify they work. Our grammar consists of two types of rules: (1) rules to handle `N` moves that decrease the stack size by `1` -- these have the form: `(q_iAq_j) -> a` for every transition of `N` from some `q_i` to `q_j` which when reading some `a` pops an `A` symbol from the stack; (2) rules to handle transitions from `(q_i,a, A)` to `(q_j, BC)`, these have the form: `(q_iAq_k) -> a(q_jBq_l)(q_lCq_k)` for all possible values of `k` and `l` in the set of states of `N`.

Quiz (Sec 1)

Which of the following is true?

1. The CYK algorithm requires a grammar to be in Greibach Normal Form.
2. The PDA one gets from class for converting a CFG to an equivalent PDA has at least three states.
3. We gave an algorithm to convert nondeterministic PDAs into deterministic ones.

Quiz (Sec 3)

Which of the following is true?

1. The algorithm from class for converting CFGs to equivalent PDAs gives a PDA with at most three states.
2. The CYK algorithm from class makes use of a CFG in Chomsky Normal Form (CNF).
3. `epsilon`-rules on a non-start variable are allowed in CNF.

Pumping Lemma for Context Free Languages

Theorem. If `A` is a context free language, then there is a number `p` (the pumping length) where, if `s` is any string in `A` of length at least `p`, then `s` may be divided into five pieces `s = uvxyz` satisfying the conditions:

1. For each `i ge 0`, `uv^ixy^iz` is in `A`,
2. `|vy| > 0`, and
3. `|vxy| le p`.

Proof. Let `G` be a CFG for our context free language `A`. Let `|V|` be the number of variables in `G`. Let `b` be the maximum number of symbols on the right hand side of a rule. So the maximum number of leaves a parse tree of height `d` can have is `b^d`. We set the pumping length to `p = b^(|V|+1)`. So if `s` is in `A` of length bigger than `p`, its smallest parse tree must be of height greater than `|V|+1`. So some variable `R` must be repeated. So we can do the following kind of surgeries on the parse tree to show Condition 1 of the pumping lemma:
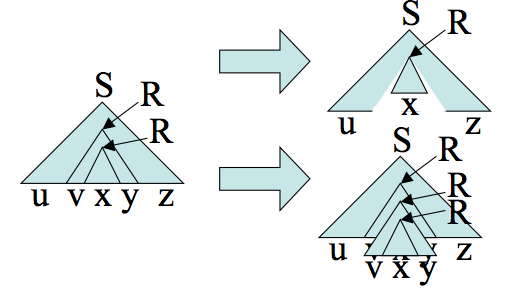Condition 2 of the pumping lemma will hold since if `v` and `y` were the empty string then the pumped down tree would be a smaller derivations of `s` contradicting our choice of parse tree. Condition 3 can be guaranteed by choosing `R` so both occurrence are among the last `|V|+1` nonterminals of the longest path in the tree. The upper `R` generates `vxy` is therefore of height at most `|V|+1` and so can generate a string of length at most `b^(|V|+1) = p`.

Remarks on the Pumping Lemma

• A stronger form of the pumping lemma for CFGs, commonly known as Ogden's Lemma, was proven by W.G. Ogden in Mathematical Systems Theory. Vol.2. 1968. pp. 191--194.
• Ogden's result states:
  Lemma. If a language `L` is context-free, then there exists some number `p > 0` such that for any string `w` of length at least `p` in `L` and every way of "marking" `p` or more of the positions in `w`, `w` can be written as `w = uvxyz` with strings `u`, `v`, `x`, `y`, and `z`, such that
  1. `x` has at least one marked position,
  2. either `u` and `v` both have marked positions or `y` and `z` both have marked positions,
  3. `vxy` has at most `p` marked positions, and
  4. `uv^ixy^iz` is in `L` for every `i ge 0`.
• Ogden's Lemma was originally used to try to understand inherent ambiguity in CFGs.
• Earlier work on showing that there are languages which are inherently ambiguous had been done by Parikh (1966) (Technical Report on same 1961). His main result (Parikh's Theorem) was to show the CFLs have a semi-linearity property.
• These results can also be used to show languages are not context-free.
• Another interesting technique to show languages are inherently ambiguous or are not context-free is based on the generating function of a language. For a language context-free language `L`, let `a_n =` the number of strings of length `n` in the language and consider the power series `f(z) = sum_(n=0)^\infty a_nz^n`. It turns out this series is algebraic (finitely many roots) if and only if `L` is unambiguous. Flajolet (1985/1987) uses this to get inherently ambiguous results.

Example use of the CFL Pumping Lemma

• Let `C={a^ib^jc^k |0 le i le j le k}`. We show `C` is not CFG using the pumping lemma.
• Suppose `C` was is CFL. Then it has a pumping length `p`. Consider the string `s=a^pb^pc^p`.
• By the pumping lemma `s` can be written as `uvxyz` satisfying the three condition of two slides ago.
• There are two cases to consider:
  1. Both `v` and `y` contain only one type of alphabet symbol. So one of `a`, `b`, or `c` does not appear in `v` or `y`. There are three subcases: (a) The `a`'s do not appear. By the pumping lemma, `uv^0xy^0z= uxz` must be in the language. This string has the same number of `a`'s but fewer `b`'s or `c`'s so cannot be in `C` giving a contradiction. (b) The `b`'s do not appear. Then either `a`'s or `c`'s must appear in `v` and `y`. If `a`'s appear, then `uv^2xy^2z` will have more `a`'s then `b`'s giving a contradiction. If `c`'s appear, then `uv^0xy^0z` will have more `b`'s then `c`'s giving a contradiction. (c) The `c`'s do not appear. Then `uv^2xy^2z` will have more `a`'s or `b`'s then `c`'s giving a contradiction.
  2. When either `v` or `y` contain more than one symbol `uv^2xy^2z` will not contain the symbols in the right order giving a contradiction.

Grammar-Based Compression Algorithms

• Besides their use in defining parsable programming languages, CFGs, can also be used in text compression algorithms.
• The Liv Zempel family of compression algorithms (Liv Zempel 1977 and 1978, Welch 1984) can be viewed as an example of this approach.
• The idea is given a string we want to compress, we try to come up with a small CFG that generates only that string. Then we encode the string by its grammar written in some suitable encoding for grammars.
• There are brute force algorithms (i.e., slow) algorithms to find the smallest CFG for a given string.
• LZ 78 is fast and known to be able to approximate the smallest grammar to within a factor `Omega(n^(2/3)/log n)` as lower bound and to within a factor an `O((n/log n)^(2/3))` factor as an upper bound.
• It is known to approximate the smallest grammar to within a `8569/8568` factor is NP-hard (Lehman and Shelat 2002).
• Charikar, et al. ( IEEE Transaction of Information Theory. 2005. pp. 2554--2576) give a compression algorithm that approximates the smallest grammar to within a factor of `O(log(n/g^star))` where `g^star` is the size of the smallest grammar for that string. (Rytter 2002 has a similar result by compressing to CNF grammars written to be AVL trees).
• We will present a simpler to describe grammar-based compression algorithm known as SEQUITUR (Nevill-Manning, Witten, Maulsby, 1997) which runs in linear time and space and also approximates the smallest grammar to within a `Omega(n^(1/3))` factor as a lower bound and `O((n/log n)^(3/4))` as an upper bound.

SEQUITUR

• For this algorithm we will make use of an auxiliary string `mbox(Aux)` that contains the results of the compression process so far.
• We will use a hash table called `mbox(Hash)` that supports deletion which will have pairs of symbols that appear in `mbox(Aux)`. This will allow fast look up of these pairs.
• We will also have a table of productions we have generated so far. The right hand side of these productions will always have length at most `2` before the final step of this algorithm is applied.
• At the start of the algorithm `mbox(Aux)` is empty, `mbox(Hash)` is empty, and our production table is empty. Let `w= w_1, ldots, w_n` be the string we'd like to compress. The algorithm proceeds on this input as follows:
  1. For `i = 1` to `n`: Add `w_i` to the end of `mbox(Aux)` and look at the last two symbols of `mbox(Aux)`. These might be a mix terminals and variables. If:
     1. The last two symbols can be found on the right-hand side of some production in our table, replace in `mbox(Aux)` these two symbols by the left hand side variable of the production in question. Mark the production as having been used more than once.
     2. The last two symbols occur somewhere else earlier in `mbox(Aux)` (we can check by looking up these two symbols in `mbox(Hash)`). Replace the two symbols with a new variable and a new production to our table consisting of this new variable going to these two symbols. Delete these two symbols from `mbox(Hash)`. Add to `mbox(Hash)` the two symbols starting from where we replaced the earlier occurrence.
     We then place the last two symbols of `mbox(Aux)` in `mbox(Hash)`. We perform the above two checks in sequence and might do both and repeat if we can still apply either.
  2. Remove rules that are only used once in the grammar by compressing them. So if `A->BC`, `B->de`, and `C->fg` and the latter two rules are only used once, then we delete these rules and add the rule `A->defg`.
  3. Finally, we output the grammar consisting of the rules in our production table together with a new start variable S that is used in the rule `S -> mbox(final value of Aux)`.

Example of Compressing with SEQUITUR

• Suppose the input string was `\a\b\b\a\b\a\b\b\a\b\b\a\b\b`. The following table shows the state of `mbox(Aux)` and the productions table after each letter is read:

  Letter	`mbox(Aux)`	Production Table	`mbox(Hash)`
  a	a	`{}`	`{}`
  b	ab	`{}`	`{ab}`
  b	abb	`{}`	{ab, bb}
  a	abba	`{}`	`{ab, \b\b, ba}`
  b	abbab becomes AbA	`{A->ab}`	`{Ab, bA}`
  a	AbAa	`{A->ab}`	`{Ab, bA, Aa}`
  b	AbAab becomes AbAA	`{A->ab` marked}	`{Ab, bA, \A\A}`
  b	AbAAb becomes BAB	`{A->ab` marked, `B->Ab}`	`{\B\A, \A\B}`
  a	BABa	`{A->ab` marked,`B->Ab}`	`{\B\A, \A\B, \B\a}`
  b	BABab becomes BABA becomes CC	`{A->ab` marked, `B->Ab`, `C->BA}`	`{\C\C}`
  b	CCb	`{A->ab` marked, `B->Ab`, `C->BA}`	`{\C\C, \C\b}`
  a	CCba	`{A->ab` marked, `B->Ab`, `C->BA}`	`{\C\C, \C\b, ba}`
  b	CCbab becomes CCbA	`{A->ab` marked, `B->Ab`, `C->BA}`	`{\C\C, \C\b, \b\A}`
  b	CCbAb becomes CCbB	`{A->ab` marked, `B->Ab` marked, `C->BA}`	`{\C\C, \C\B}`

• Initially, we get the grammar `{A->ab`, `B->Ab`, `C->BA`, `S->\C\Cb\B}`
• After removing rules that were used only once we have `{A->ab`, `B->Ab`, `S->\B\A\B\Ab\B}`.
• As a crude, not too efficient example of how we could encode this... If we used `R` to denote the start of a rule, # followed by a sequence of digits for `n` to denote the `n` variable, and let `t` denote the terminal `t` unless `t` is `R`, '#', '\', or a digit in which case we use `\\t` is used to denote `t`, then the string `\a\b\b\a\b\a\b\b\a\b\b\a\b\b` might be compressed as RabR#0bR#1#0#1#0b#1.
• We don't have to list the left hand side variable for a rule, because each variable appears at most once on the left hand side and we can count `R`'s to figure out which rule we are.
• It works better on longer strings. For example, a string of 64 `a`'s might be encoded as RaaR#0#0R#1#1R#2#2R#3#3R#4#4, a string of length 28.