Outline

• State Minimization
• Homework Problems
• Building new NFAs out of Old Ones
• Regular Expressions

State Minimization

• We say two states `p`, `q` of a DFA `M` are indistinguishable if `delta^star(p,w) in F` implies `delta^star(q,w) in F` and `delta^star(p,w) !in F` implies `delta^star(q,w) !in F`.
• Otherwise, `p`, `q` are said to be distinguishable.
• Let `p~_I q`,if `p` and `q` are indistinguishable. Notice this is an equivalence relation.
• We now present an algorithm to find the minimal DFA equivalent to `M`.
• The idea is to first compute the equivalence classes of the indistinguishable equivalence relation. Then make one state for each equivalence class, and make an appropriate new transition function.

Procedure for Equivalence

1. Remove all inaccessible states. This can be done by checking for each state if there is a simple path from the start state to it.
2. Consider all pairs `(p,q)` of states. If `p in F` but `q !in F` or vice versa, then mark the pair `(p,q)` distinguishable.
3. Repeat until no previously unmarked pairs are marked:
   1. For all pairs `(p,q)` and all `a in Sigma`, compute `delta(p,a) = p_a` and `delta(q,a) = q_a`. If the pair `(p_a,q_a)` is marked as distinguishable, mark `(p,q)` as distinguishable. Idea: if in `p` `q` on the same letter you transition to distinguishable states then `p` and `q` must be distinguishable.

Procedure to Build Minimal Automaton

1. Use procedure of last slide to generate state equivalence classes for original automata.
2. For each equivalence class `[p] = {q | p~_I q}` create a new state.
3. For each transition rule `delta(r,a)=s` of the original machine, add a transition `delta([r],a)=[s]`.
4. The initial state of the new machine is `[q_0]` where `q_0` was the state of the machine we are trying to minimize.
5. The final states of the new machine is the set `{[f] | f in F}`.

The first procedure for minimizing finite automata was given in Huffman 1954 (J. Franklin Institute. Vol 257. Iss. 3-4).

Our procedure above probably runs in quadratic time, the best known algorithm is `O(n log n)` due to Hopcroft 1971.

Example

• You can use JFLAP to take an NFA convert it to a DFA and then minimize the result.
• For example, we might start with the following NFA:
  
• We can then use JFLAP to get the following DFA (JFLAP will step you through the procedure if you like so you can learn it):
  
• In the above, I added the trap state with label emptyset and moved around the states to make it prettier looking (I hope).
• Finally, we can convert this last DFA to the minimal DFA:
  
• Since this is a DFA we know we can code it in C or Java. It is also as small as possible so it will be easier to code.

Indistinguishability and the Myhill-Nerode Theorem

• We used the notion of two states being distinguishable in our minimizing construction. One can similarly define the notion of two strings `u`, `v` being distinguishable with respect to a language if there are strings `t`, `w` such that `tuw in L` but `tvw !in L`.
• If two strings are not distinguishable we say they are indistinguishable with respect to `L`. We write `[v]_L` for the equivalent class of all strings equivalent to `v`.
• We can define a binary operation `[v]_L*[w]_L = [vw]_L` which is easy to show is associative with empty string as an identity `[epsilon]_L[v]_L = [v]_L[epsilon]_L =[v]_L`.
• The equivalence classes imbued with this operation are called the syntactic monoid of `L`.
• Notice in the case where one of the two strings is an alphabet symbol, the operation above can be viewed as a transition function: `delta([v]_L, a) = [va]_L`.
• If `v in L` then all members of `[v]_L` will be in `L` so it makes sense to call these the accept states of this automaton.
• We can let the set of equivalence classes `[v]_L` be our states.
• If `L` has a finite number of equivalence classes then this machine will be a DFA and `L` will be a regular language.
• If a language is regular, we can take a DFA for it and minimize it. For state `q`, `q'` of this machine, let `v_q` and `v_(q')` be strings that takes one to these states. Then `v_q` and `v_(q')` must be distinguishable with respect to `L`. On the hand, if two strings map one to the same state `q` then they will be indistinquishable with respect to `L`. So the states of this machine exactly correspond to the equivalence classes of `L` and so will be finite.
• This is the content of the Myhill Nerode theorem which is due to Nerode 1958 building on a paper of Myhill 1957: A language is regular iff the set of equivalence classes of `L` with respect to indistinguishability is finite.
• It shows the automata one gets from our construction is unique up to a renaming of states.

Homework Problems (Sec1 and Sec2 - same problems)

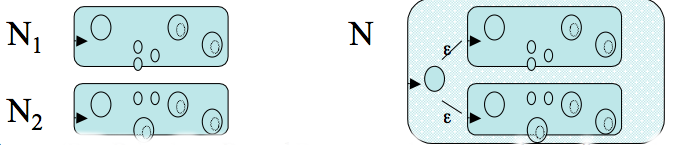
Problem 3. Apply the Cartesian product construction to (i) and (j) of exercise 1.6 to obtain an automata recognizing the union of their languages.

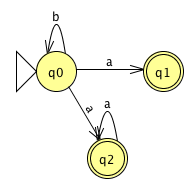
Answer. The following is an automaton which recognizes strings every odd position is a 1 (solving i):

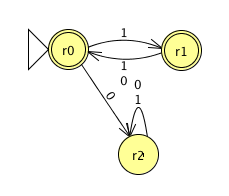
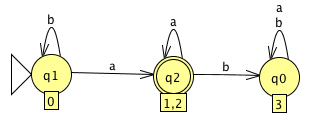
And the following is an automaton which recognizes those string which have at least two 0's and at most one 1 (solving j):

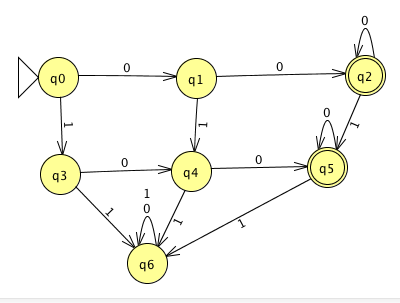
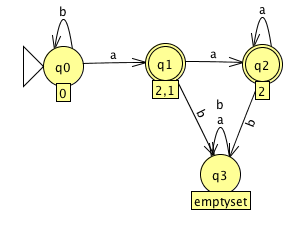
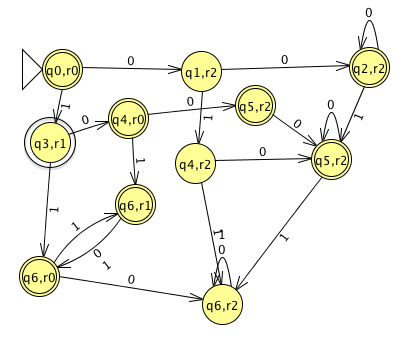
The machine coming from the Cartesian product construction where we consider only those states which are reachable from the start state is:

Problem 4. Consider the variant of Exercise 1.38 where rather than being in the language occurs if every possible state that M could be in after reading input x is accepting, we instead only require more than half of the states be accepting. Prove that the resulting class also recognizes exactly the regular languages.

Answer. Let PReg (probabilistic regular) denote the class of languages recognized by machines of the above kind. There are two parts to this problem: We need to show Reg `subseteq` PReg and PReg `subseteq` Reg. The fact that we used the word "exactly" requires us to prove both directions. To see Reg `subseteq` PReg, let `L` be a regular language. By definition, `L=L(M)` for some DFA `M = (Q, Sigma, delta, q_0, F)`. Consider the machine `N = (Q \cup {q'}, Sigma, delta', q_0, F)` where `delta'` and `F'` are defined as follows. For any `q in Q` and `a in Sigma` define `delta'(q, a) = {delta(q,a)}` this is a well-defined mapping from `Q times Sigma -> P(Q \cup {q'})`. For we define `delta'(q, epsilon) = {q'}` for some new state `q'` not in `Q`. Define `delta'(q', x) = {q'}` for `x in Sigma cup {epsilon}`. Observe by induction that `delta'^\star(q, w) = E(delta^\star(q,w)) ={delta^\star(q,w), q'}` and so consists of at most one accepting state. Now notice `w in L` iff `delta^\star(q_0,w) = f` for some `f in F` iff `delta'^\star(q_0,w) = {f,q'}` for some `f in F`. If less than half the states in `delta'^\star(q_0, v) = {s,q'}` are accepting then none of them must be accepting. Hence `s !in F` so `v !in L`. Similarly, if at least half of the states in `delta'^\star(q_0, v)` then `s in F`, so `v in L`. Therefore `N` shows `L` is in PReg. On the other hand, suppose `L` is a language in Preg via some machine `N`. Apply the Power set construction to `N = (Q, Sigma, delta, q_0, F)` to get a machine `M = (P(Q), Sigma, delta', {q_0}, F')`. Rather than define `F'` as in the original construction define
`F' = {X | X \subset P(Q) mbox( at least half of X elements are accepting)}`. The resulting machine is a DFA recognizing the same language as `N`.

Regular Expressions

• In arithmetic, we can use the operations `+` and `cdot` to build up expressions such as: `(5 + 3) cdot 4`.
• Similarly we can use the regular operations to build up expressions describing regular languages.
• For instance, `0(0 cup 1)^star`.
• This means the language which results from concatenating the language containing 0 with the language of `(0 cup 1)^star`. This in turn is the star of the union of the two languages one containing just `0`; the other containing just `1`.
• These kind of expressions are used in many modern programming languages: Perl, PHP, Python, Java, AWK, GREP.

Formal Definition of a Regular Expression

We say that `R` is a regular expression if `R` over some alphabet `Sigma` is:

1. `a` for some symbol `a` in the alphabet `Sigma`.
2. `epsilon`.
3. `emptyset`.
4. `(R_1 cup R_2)` where `R_1` and `R_2` are regular expressions. `R_1 + R_2` is used by JFLAP, most programming languages use `(R1 | R2)`.
5. `(R_1R_2)` where `R_1` and `R_2` are regular expressions.
6. `(R_1)^star` where `R_1` is a regular expression.

We write `R^+` as a shorthand for `R\ R^star`. Notice also we tend to be lazy on parentheses even thought to be fully well-formed everything has to be completely parenthesized.

We write `L(R)` for the language given by the regular expression.

Regular expressions were first considered in Kleene (1956).

In older books, you sometimes see regular expressions called rational expressions.

Examples of the Definition

• `0^star10^star={w| w \ mbox{contains a single} \ 1}`
• `(01 cup 10) = {01, 10}`
• `((0 cup 1) (0 cup 1))^star = {w| w \ mbox{is of even length}}`
• `(epsilon cup 0)(epsilon cup 1)= {epsilon ,0,1,01}`
• `1^star emptyset = emptyset`
• `emptyset^star = {epsilon}`

In a programming language like say PHP or Perl you might use things like: "\.|\,|\:|\;|\"|\'|\`|\]|\[|\{|\}|\(|\)|\!|\||\&" to match against, for instance, the punctuation symbols you want.

If you want to see regular expressions gone wild check out the Perl solution to the 99 bottles of beer song.

Some Regular Expression Identities

The following identities (`equiv` here meaning have the same language) are not too hard to verify:

• `(R cup R) equiv (emptyset cup R) equiv (R cup emptyset) equiv (epsilon R) equiv (R epsilon) equiv R`.
• `(R cup S) equiv (S cup R)`
• `R(S cup T) equiv (RS cup RT)` and `(S cup T)R equiv (SR cup TR)`.
• `R(ST) equiv (RS)T`
• `(R cup S)^\star equiv (R^\star S)^\star R^\star`
• `(R S)^\star equiv \epsilon \cup R(S R)^\star S`
• For any `n ge 1`, `R^\star equiv (epsilon cup R cup R^2 cup ... cup R^(n-1))(R^n)^\star`

Viewing emptyset as `0`, empty string as `1`, concatenation as multiplication, union as plus, the above show the regular expressions are a so-called semi-ring, and perhaps motivates why they are sometimes called rational expressions. It is not a ring because given `R` we can't easily define a regular expression `R'` such that `R cup R' equiv emptyset`.

Semi-rings don't typically have a star operation (there is a something called a star semi-ring). To reduce to the situation where one can get rid of star, one can look at languages which have the finite power property. That is, languages for which `L^\star = epsilon cup L cup ... cup L^(n-1)` for some `n ge 1`. Algorithms for checking this property have been given by Hashiguchi and Simon.

Equivalence with Finite Automata

• We want to show that a language is regular if and only if some regular expression describes it.
• We will do this in two steps:
  • Prove if a language is described by a regular expression, then it is regular
  • Prove if a language is regular, then it is described by a regular expression.

Proof that regular expression implies regular

• The proof is by induction on the complexity (number of uses of union, `star`, or concatenation) of the regular expression. In the base case, we have regular expressions which make no use of union, `star`, or concatenation.
  1. Let `R = a` for some `a` in `Sigma`. Then the following NFA recognizes the languages contain only a:
     
  2. Let `R = epsilon`. Then the following NFA recognizes it:
     
  3. Let `R = emptyset`. Then the following NFA recognizes it:
     

Proof cont'd

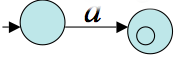
Assume now the result holds for languages for which the total number of uses of union, `*`, or concatenation is at most `n`. Consider `R` a regular language of complexity `n+1`. There are three cases to consider:

1. `R` is of the form `(R_1 cup R_2)` where `R_1` and `R_2` are regular expressions of complexity `leq n`. By induction let `N_1` and `N_2` be the machines for `R_1` and `R_2`. Define `N` for `R` as:
   
2. `(R_1R_2)` where `R_1` and `R_2` are regular expressions of complexity `leq n`. By induction let `N_1` and `N_2` be the machines for `R_1` and `R_2`. Define `N` for `R` as:
   
3. `(R_1)^star` where `R_1` is a regular expression of complexity `leq n`. By induction let `N_1` be the machine for `R_1`. Define `N` for `R` as: