Nondeterministic Finite Automata
CS154
Chris Pollett
Feb. 11, 2013











CS154
Chris Pollett
Feb. 11, 2013
If `A_1` and `A_2` are two regular languages, so is their union `A_1 cup A_2`.
Proof. Let `M_1=(Q_1, Sigma, delta_1, q_1, F_1)` and `M_2 =(Q_2, Sigma, delta_2, q_2, F_2)` be the DFAs recognizing languages `A_1` and `A_2`. We would like to make a new DFA, `M`, which simultaneously simulates both `M_1` and `M_2` and accepts a string `w` if either of `M_1` and `M_2` accepts. To simulate both machines at the same time we use a so-called "Cartesian product construction". To do this let `Q = Q_1 times Q_2`. `M`'s alphabet is `Sigma` like that of `M_1` and `M_2`. Define `delta((q, q'), a) = (delta_1(q,a), delta_2(q',a))`. Let the start state of `M` be `(q_1, q_2)`. Finally, let `F = (F_1 times Q_2 )cup (Q_1 times F_2 )`. Verify at home that `M` has the desired properties.
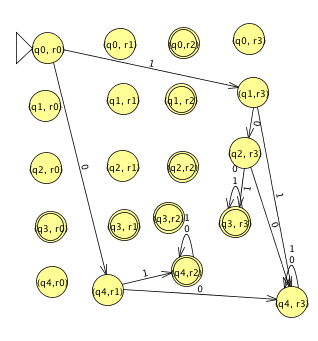
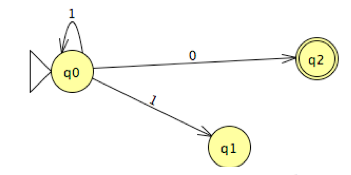
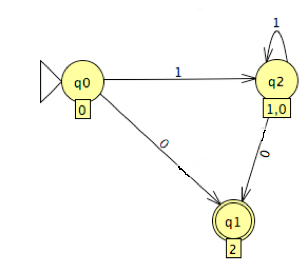
Which of the following is true?
Which of the following is true?
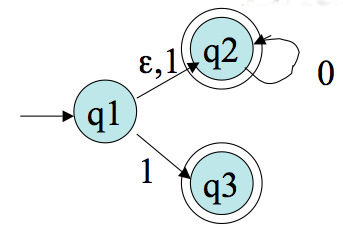
Theorem Any language recognized by an NFA is recognized by some DFA.
Proof: Given an NFA `N= (Q, Sigma, delta, q_0, F)` we want to simulate how it acts on a string `w` with a DFA, `M= (Q', Sigma, delta', q_0', F')`. The idea is we want to keep track of what possible states it could be in after reading the first `m` characters of `w`. Let `Q'= P(Q)`, the power set of `Q`. The alphabet is the same. For each `R in Q'` (i.e., `R subseteq Q`) and `a in Sigma`, let `delta'(R, a) = {q in Q | q in E(delta(r,a)) \ mbox{for some} \ r in R}`. Here `E(q')` is the set of states reachable from `q'` following 0 or more `epsilon` transitions, for a set of states `Q''`, `E(Q'')` is the union of `E(q'')` for `q'' in Q''`. Let the new start state be `q_0'=E(q_0)`. Let `F' = {R in Q'| R \ mbox{contains an accept state of} \ N}`.
This construction is from the original NFA paper of Rabin and Scott (1959).