Outline

• The Formal Definition of DFA again
• Example
• HW Problems
• Regular Languages
• Traps States
• Walks on Automata
• Product Construction

Formal Definition

At the end of Monday, we gave the following formal definition of deterministic finite automata (DFA):

• A deterministic finite automaton is a 5-tuple `(Q, Sigma, delta, q_0, F)`, where
  1. `Q` is a finite set called the states.
  2. `Sigma` is a finite set called the alphabet.
  3. `delta:Q times Sigma rightarrow Q` is the transition function.
  4. `q_0 \in Q` is the start state.
  5. `F subseteq Q` is the set of accept states.
• The transition function tells us if we are in a given state reading a given symbol what is the next state to go to.

Example of the Definition

• Consider the machine:
  
• The corresponding five tuple for this machine has:
  1. `Q = {q_1, q_2, q_3}`,
  2. `Sigma = {0, 1}`,
  3. `delta` is the function given by:
     `(q_1, 0) mapsto q_1`, `(q_2, 0) mapsto q_3`, `(q_3, 0) mapsto q_2`,
     `(q_1, 1) mapsto q_2`, `(q_2, 1) mapsto q_2`, `(q_3, 1) mapsto q_2`
  4. `q_1` as the start state,
  5. `F = {q_2}`.

Homework Problems (Sec 1)

Problem 1. Prove by induction that, `sum_(i=0)^n (3i^(2) +3i +1) = (n+1)^3`. Show carefully that this sum is `Theta(n^3)`.

Answer. As an aside whenever you see a sum like the above you should be suspicious that it comes from a telescoping series -- the technique of the ancients like Archimedes to do integration before the development of differentiation. A telescoping series is one of the form: `sum_{i=0}^{n}(a_(i+1) - a_i) = a_(n+1) - a_0`. The equality is because all except the first and last term in this series cancel. In particular, `sum_(i=0)^n ((i+1)^3 - i^3) = (n+1)^3`, but if we expand each summand we get `(3i^(2) +3i +1)`. To see that the original statement is true by induction, we need to show that it holds when `n=0` and that whenever it hold for some natural number `n > 0` it also holds of `n+1`. First consider the case when `n=0`. Then the sum above is:
`sum_(i=0)^0 (3i^(2) +3i +1) = 3 cdot 0^2 + 3cdot 0 + 1 = 1 = (0 + 1) ^3.`
Hence, the `n=0` case holds. Suppose the statement is true up to some `n > 0`. Consider the sum up to `n+1`:
`sum_(i=0)^(n+1) (3i^(2) +3i +1) = (3(n+1)^(2) +3(n+1) +1) + sum_(i=0)^n (3i^(2) +3i +1)`
Using the induction hypothesis we have:
`sum_(i=0)^(n+1) (3i^(2) +3i +1) = (3(n+1)^(2) +3(n+1) +1) + (n+1)^3`
`quad = (n+1)^3 + 3(n+1)^(2) +3(n+1) +1 = ((n+1) + 1)^3 = (n+2)^3.`
Hence, the induction hypothesis holds and the statement is proven.

Given `sum_(i=0)^n (3i^(2) +3i +1) = (n+1)^3`, we next want to show the sum on the LHS is `Theta(n^3)`. According to the definition, this means we need to show `(n+1)^3 = O(n^3)` and `n^3 = O((n+1)^3)`. To show the first statement, notice when `n geq 1` we have `n+1 leq n + n = 2n` and so `(n+1)^3 leq (2n)^3 = 8n^3`. So for all `m geq N = 1`, if `c=8`, `(m+1)^3 leq c m^3`. Therefore, `(n+1)^3 = O(n^3)`. To see the second statement notice `n leq n+1` and so since cubing is a nondecreasing function, `n^3 leq (n+1)^3`. So for all `m geq N = 1`, if `c=1`, `m^3 leq c (m+1)^3`. Therefore, `n^3 = O((n+1)^3)`.

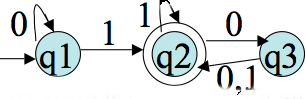
Problem 3. Draw a finite automata that accepts all string over `{0,1}` that have an even number of `1`'s.

Answer. In designing a finite automata, the first question we should ask is whether the start state is accepting or not. In this case, the empty string has zero 1's in it and zero is and even number, so the empty string should be accepted, and hence, the start state should be accepting. Next we should ask for each alphabet symbol `a`, if I had started with that alphabet symbol `a`, is there a string `v` such that my behavior on `epsilon v` should be different from `a v`. For the question at hand the machines behavior on `epsilon v` and `0 v` should be the same however for `epsilon v` and `1 v` the behavior should not always be the same. For example, if `v = epsilon`, then `epsilon v = epsilon ` is in the language, but `1 v = 1` is not. From this, we get that on a `0` we should remain in the same state, but on a `1` we should go to a different state. Continuing in this fashion, we could come up with the following machine:

Homework Problems (Sec 3)

Problem 2. Using the pigeonhole principle, show that every undirected graph without loops with two or more nodes contains two nodes that have equal degree.

Answer. The (injective) pigeonhole principle says that for every map `f: A->B` where `|A| > |B|`, there exists `x ne y in A` such that `f(x) = f(y)`. At home you should try to prove this statement by induction. Suppose we have an undirected graph `G = (V, E)` where `|V| geq 2` which has no loops. Recall for `v in V` the degree of `v`, `deg(v)`, is the number of edges leaving `v`. Since we are assuming there are no loops, each edge must be connected to some other vertex (we use vertex and node interchangeably). So the `deg(v) < |V|`. We can define a function `f:V-> {0,..., |V| - 1}` by `f(v) mapsto deg(v)`. Consider the case where there is a `v` such that `deg(v)=0`. If some other vertex `v'` also has `deg(v') = 0` we are done. Suppose not, then `f` restricted to `V - {v}` is a map from `V-{v} -> {1,... , |V| - 2}`. Since `|V-{v}| = |V| - 1`, by the pigeonhole principle we can find `v' ne v'' in V -{v}` such that `deg(v')=f(v')=f(v'')=deg(v'')`. Now suppose there is no `v in V` with `deg(v) = 0`. Then `f:V-> {1, ...,|V| - 1}`. I.e., it is a map of a set of size `|V|` into one of size `|V| -1`, so by the pigeonhole principle we can find `v' ne v'' in V -{v}` such that `deg(v')=f(v')=f(v'')=deg(v'')`. QED.

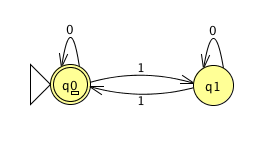
Problem 4. Write down the automata of the previous problem formally as a 5-tuple.

Answer. The following is a possible state diagram that solves Problem 3:

We can write this machine a 5-tuple: `(Q, Sigma, delta, q_0, F)` if we set:

• `Q = {q_0, q_1}`
• `Sigma = {0, 1}`
• `delta : Q times Sigma -> Q` according to the mappings:
  `(q_0, 0) mapsto q_0`
  `(q_0, 1) mapsto q_1`
  `(q_1, 0) mapsto q_1`
  `(q_1, 1) mapsto q_0`
• `F = {q_0}`.

Implementing Finite Automata -- Base Class

• Suppose we had the job of implementing a finite automata in Java.
• Typically, we would want to process strings according to how the finite automata would process them.
• To make our set-up as flexible as possible we should probably have a base class that implements the core string processing algorithm.
• Then in sub-classes specify the transition function, start state, and final states to use.
• An example base class might be:

  public abstract class Automata
  {
      public Automata()
      {
      }
  
      public void setState(int state)
      {
          currentState = state;
      }
  
      public boolean processString(String w) 
      {
         for(int i = 0; i < w.length(); i++)
         {
             currentState = delta(currentState, w.charAt(i));
         }
         boolean accept = finalState(currentState);
         return accept;
      }
  
      public abstract int delta(int state, char c);
      public abstract boolean finalState(int state);
  
      int currentState;
  }
  

Implementing Finite Automata -- Specific Automata

• Now if we wanted to implement the automata of a couple slides ago we could write:

  public class TestAutomata extends Automata
  {
      public TestAutomata()
      {
      }
  
      public int delta(int state, char c)
      {
          int outState = 1;
          switch(state)
          {
              case 1:
                  if(c == '0') 
                  {
                      outState = 1;
                  } 
                  else 
                  {
                      outState = 2;
                  }
              break;
  
              case 2:
                  if(c == '0')
                  {
                      outState = 3;
                  }
                  else 
                  {
                      outState = 2;
                  }
              break;
  
              case 3:
                  outState = 2;
              break;
          }
          return outState;
      }
  
      public boolean finalState(int state)
      {
          return (state == 2) ? true : false;
      }
  
      public static void main(String args[])
      {
          TestAutomata test = new TestAutomata();
          test.setState(1);
          if(args.length == 0 ){
              System.out.println("It is not recognized by this automata.");
          }
          System.out.println("Checking the string "+ args[0]);
          if(test.processString(args[0])) 
          {
              System.out.println("It is recognized by this automata.");
          }
          else
          {
              System.out.println("It is not recognized by this automata.");
          }
      }
  }
  

Comments on Code

• Notice the only memory requirements besides the input string are all constant. For example, 4 bytes to store the int for the currentState -- so DFAs are very memory efficient.
• Notice also to determine if the string was in the language we made a single scan on the input string and at each step while scanning only process a fixed number of instructions.
• So the processing was linear time in the input length. i.e., very fast.

Formal Definition of Accepting a String

• Let `M= (Q, Sigma, delta, q_0, F)` be a finite automaton and let `w=w_1 w_2 ldots w_n` be a string. Then `M` accepts `w` if a sequence of states `r_0 r_1 ... r_n` in `Q` exist satisfying:
  1. `r_0=q_0`
  2. `delta(r_i, w_(i+1)) = r_(i+1)`, for `i=0,1, ldots , n-1`,
  3. `r_n in F`.
• That the string `0100` is accepted by the automata of a few slides ago is witnessed by the sequence of states `q_1 q_1 q_2 q_3 q_2`. Notice this is a walk on the automata viewed as a labeled graph.
• We write `L(M)` for the language that `M` accepts. That is, those strings that `M` accepts.
• Given a set of strings `S`, we say `M` recognizes `S` if `L(M)=S`.
• So `M_1` of a couple slides back recognizes `{ w | w \ mbox{contains at least one 1 and an even number of 0s follow the last 1}}`
• A language is called a regular language if some finite automaton recognizes it.

The Extended Transition Function

• Let `M= (Q, Sigma, delta, q_0, F)` be a finite automaton and let `w=w_1w_2 ldots w_n` be a string.
• We define the extended transition function `delta^star:Q times Sigma^star rightarrow Q` inductively:
  1. `delta^star(q, epsilon) rightarrow q`
  2. `delta^star(q, wa) rightarrow delta(delta^star(q,w),a)`
• Intuitively, the equation `delta^star(q, w) =q'` tells us that if we are in state `q` when we begin to process the string `w`, then after processing `w` we will be in state `q'`.
• An equivalent to the last slide's way to define `M` accepts `w` is to say, `M` accepts `w` if for some `q in F` we have `delta^star(q_0, w)=q`. i.e., we start in the start state `q_0`, process `w`, and end up in an accept state.
• In more formal treatments of automata theory, the extended transition function can be used to define the so-called transformational monoid of the automata.
• Basically, we view strings as acting on the set of states. i.e., a string `v` defines a functions from `Q -> Q` via `v(p) = delta^star(p, v)=q`. Composition is then a binary operation with the function defined by the empty string serving as an identity.

Designing Automata

• Suppose we want to recognize the language that consists of an odd number of 1s.
• One approach is to "pretend to be the automaton".
• You get symbols from {0,1} one by one.
• Ask how much of the string so far do we need to remember in order to decide whether to accept or not? In this particular case, we just need to remember if we are currently even or currently odd.
• Now we make each of these possibilities states. Next we pretend we are in one of the states and see a symbol. What do we do?
  
• Finally, we figure out what our accept and final states are:
  

Trap States

• For DFA, we require `delta` to be a total function.
• This means for every state `q` and every alphabet symbol `a`, `delta(q,a)` must return some state `q'`.
• That `delta` is total will force `delta^star` to be total as well.
• Consider the problem of designing an automaton for the language: `{w | w = a^nb \ mbox{for some}\ n geq 0}`.
• On a string like `aabab`, after the third `a` we know the string is not in the language; nevertheless, since the transition function is total we still need to continue processing the string until it is done.
• This can be done with a trap state, which has a loop back to itself for every alphabet symbol.

Walks on Automata

Theorem

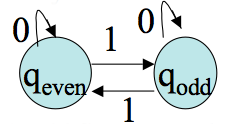
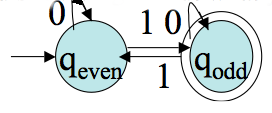
Let `M= (Q, Sigma, delta, q0, F)` be a DFA, and GM be its associated transition graph. Then for every `q_i`, `q_j` in `Q` and `w` in `Sigma^star` , `delta^star(q_i,w) = q_j` iff there is in GM a walk with label `w` (that is, the edge labels written down as a string are `w`) from `q_i` to `q_j`.

Proof. We give a proof by induction on the length `n geq 0` of `w`. Notice `delta^star(q, epsilon)=q` corresponds exactly with a walk of length `0` in GM . So the `|w|=0` case holds. Assume the statement is true up to some `n`. Let `w=va` where `|v|=n`. (The induction step case.) Suppose `delta^star(q_i,v) = q_k` . By the induction hypothesis there is a walk `W` of length `n` in GM from `q_i`,to `q_k`. If `delta^star(q_i,w) = q_j` we must have `delta^star(q_i,w) = delta (delta^star(q_i,v), a) = q_j` by the definition of `delta^star.` So we have `delta(q_k,a) = q_j`. Thus, if we add to `W` the edge `(q_k, q_j)`, the label on the resulting walk will be `va=w` as desired. This new walk has length `n+1`. It is also not hard to turn this argument around to show if one stated with a walk of length `n+1` with label `w`, that one could show `delta^star(q_i,w) = q_j`. You should do this at home.

Regular Operations

• Just as the natural number are closed under operations like addition and multiplication, the regular languages enjoy some closure properties:
  • Union `A cup B = {x| x in A or x in B}`.
  • Concatenation `AB = {xy | x in A ^^ y in B}`
  • Star `A^star = {x_1 x_2 ldots x_k| k geq 0 \ mbox{and each} \ x_i in A }`
• This closure conditions require proof. We will prove the first one today. We will show the last two after we introduce nondeterministic finite automata.