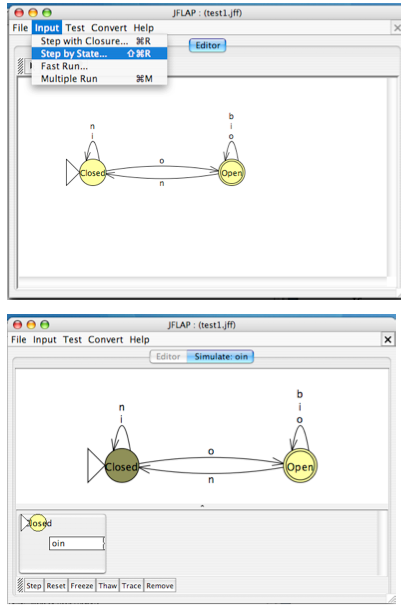
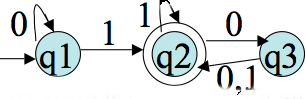
Finite Automata
CS154
Chris Pollett
Feb. 3, 2014











CS154
Chris Pollett
Feb. 3, 2014
Which of the following is true?
Which of the following is true?
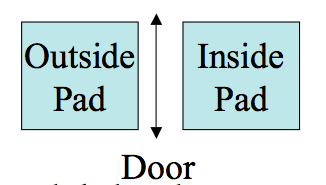
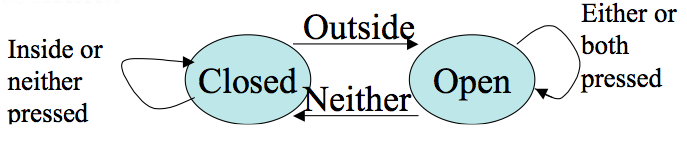
| Neither | Outside | Inside | Both | |
|---|---|---|---|---|
| Closed | Closed | Open | Closed | Closed |
| Open | Closed | Open | Open | Open |