Outline

• Ways of Building Bigger Machines
• HW Problems
• More JFLAP
• Church-Turing Thesis

Transducers

• We now have defined it means for a TM to recognize and to decide a language.
• Another useful thing that we can do with a Turing Machine is to compute functions. We call these kinds of TMs tranducers.
• For example, we might need to compute a function to convert the problem of deciding membership for one language into the problem of deciding membership in another language.
• We say a function `f` with domain `D` is computable, if there is some TM `M` which when started on inputs `w` from `D`, halts with `f(w)` on the tape.
• We next describe a TM which on `w` computes `w square w`. The book shows how to do several languages which we showed couldn't be done on a PDA.

Ways of Building Larger Turing Machines

• We now turn our attention to how to build larger Turing Machines from little Turing Machines.
• You can think of this process as very much like building larger and larger functions starting with little functions.

A Simple Turing Machine

• The transition function is the most important part of a TM's description.
• We will sometimes use a graphical notation to describe TM's and in particular this function.
• Given `a in Sigma` define a machine `M_a ={{s,h}, Sigma, Sigma\cup{ square }, delta, s, {h}}`, where for each `b in Sigma\cup{ square }`, `delta(s,b) = (h, a, R)`.
• That is, if `a` is a symbol, the only thing `M_a` does is write that symbol, move right, and halt.
• Similarly, for `a` either `L` or `R` we can build a machine such that the only thing `M_a` does is either move one square left or right.

Building Bigger TMs

• Given three TMs with a common alphabet: `M`, `N`, `P`, we can build a new machine `M'` which operates as follows:
  • Start in the initial state of `M`; operate as `M` until `M` would halt, then
  • If the currently scanned symbol is a `b`, start `N`
  • If the currently scanned symbol is an `a`, start `P`.
  • Halt otherwise.
• Diagrammatically we write:
  
• As an exercise you should work out what `M'`'s transition function would look like.
• This shows TMs can do if-then-else statements
• If one of `N` or `P` was instead a loopback to `M` we would have a while- loop. Hence, it should become clear we are starting to be able to simulate many programming language constructs.

More on Diagrams

• Similar to the if-else type diagram of the last slide we can have diagrams like:
  `M -> N`
• Notice there is no label on the arrow. This means that if machine M is about to transition to its halt state `h` we instead have it transition to the start state of `N`.
• We can also generalize the two branch construction of the previous slide to any fixed finite number of branches. This would allow us to simulate switch-case like commands.

Examples

• We sometimes abbreviate `M_R` as `R` and `M_a` as `a`. We might also make abbreviations like `Ra` for the machine which does `M_R`, then reading any symbol writes an `a`. Similarly, we might have `\R\R` or `La`.
• Let `mbox{!=}a` denote all the symbols in `Sigma` except `a`.
• Here is a machine `R_\square` that scans right to the first space:
  
• Here is a machine `L_\square` that scans left to the first space:
  

More Examples

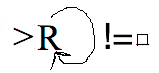
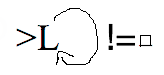
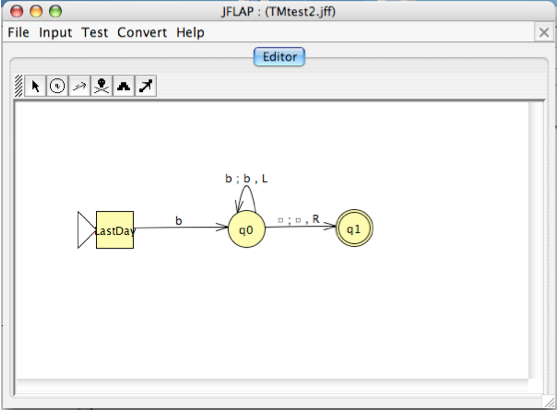
Here is a machine which when started with a string `w` on the tape halts with `w\square w` on the tape.

• In the above, `a` is some symbol of the tape alphabet. Each place we use it though we mean the same alphabet symbol.
• The loop back to R is somewhat awkwardly drawn, we do all of `\square(R_square)^2a(L_square)^2a` before looping.
• Suppose the input was `bcd`. Here are some of the significant tape configurations:

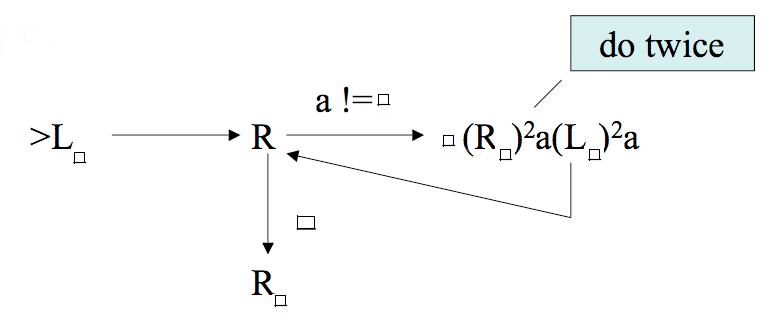
  `q_{mbox{start}}bcd`
  `q_{mbox{done L rewind}}\square bcd`
  `\square q_{mbox{done R}}bcd`
  `\square q_{mbox{read }b mbox{ wrote space}} cd`
  `\square \square cd \square q_{mbox{right two spaces wrote b}} b`
  `\square q_{mbox{left two spaces wrote b}}bcd \square b`
  `\square b q_{mbox{done R}}cd \square b`
  `\square b q_{mbox{read }c mbox{ wrote space}}\square d \square b`
  `\square b \square d \square b q_{mbox{right two spaces wrote c}}c`
  `\square b q_{mbox{left two spaces wrote c}}c d \square b c`
  `\square b c q_{mbox{read }d mbox{ wrote space}} \square \square b c`
  `\square b c\square \square b c q_{mbox{right two spaces wrote d}}d `
  `\square b cq_{mbox{left two spaces wrote d}} d \square b c d `
  `\square b c d q_{mbox{done R}} \square b c d `
  `\square b c d \square b c d q_{mbox{done advance right space and halted}} \square`
  

Homework Problems

Problem 1. Show step-by-step how the string 0001010001 would be compressed by the SEQUITUR algorithm.

Answer. The following table shows the state of `mbox(Aux)` and the productions table after each letter is read:

We next remove any rule used only once (an unmarked rule), and add a rule `S -> mbox(Aux)`. This gives the grammar. `{S->0A0101A1, A->00}`. This could be represented as the string R\0\0R\0#0\0\1\0\1#0\1.

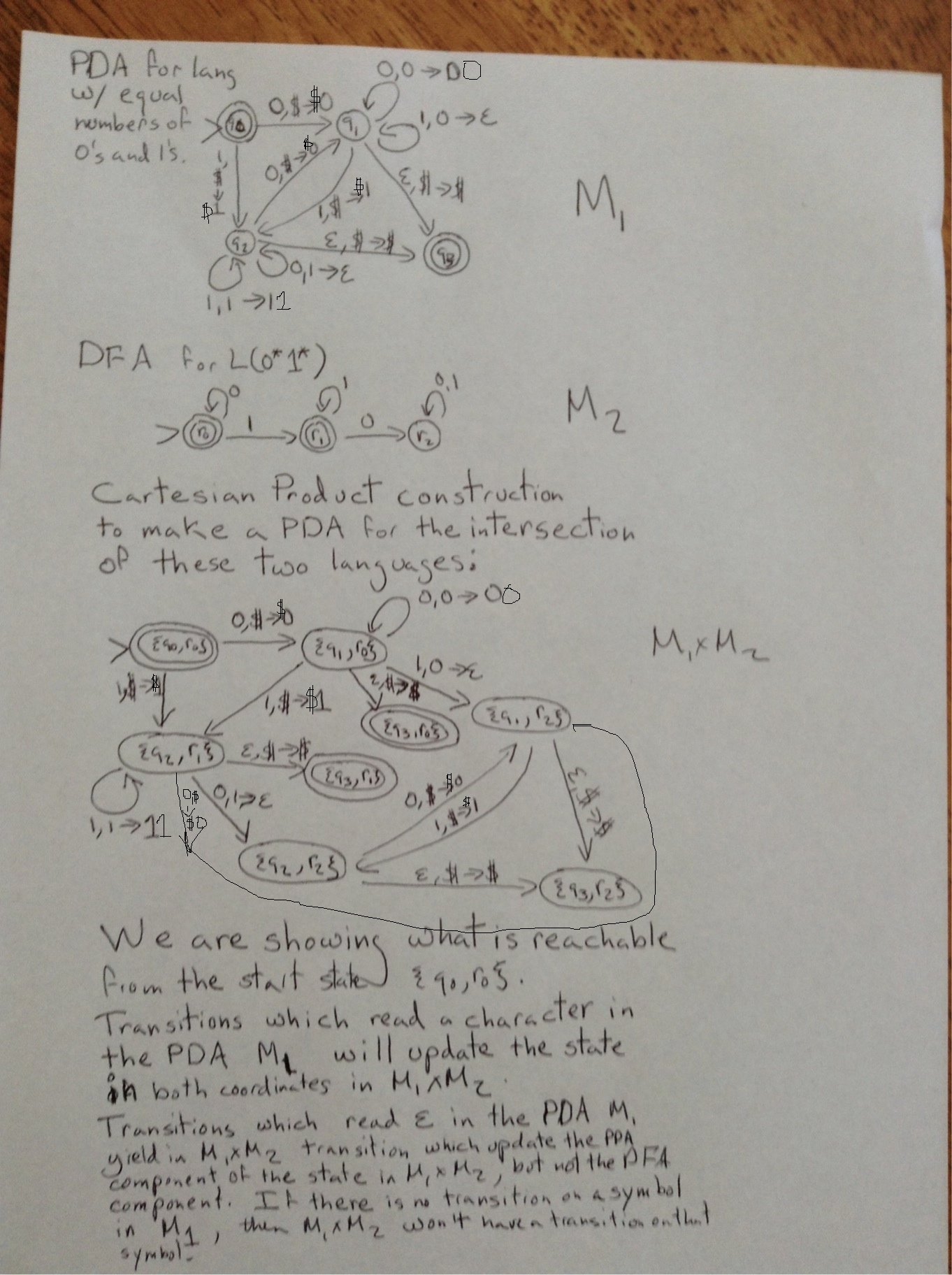
Problem 2. Draw a PDA for the language L over `{0,1}` consisting of strings with an equal number of 0's and 1's. So 010011 would be in this language. Next draw a DFA recognizing `0^\star1^\star`. Use the algorithm from class to draw a PDA for the intersection of these two languages.

Here is an image of the relevant diagrams and resulting construction:

JFLAP

• JFLAP supports building larger machines out of smaller machines.
• If one clicks on the Turing Machine button in JFLAP, one can start building a Turing Machine.
• The two rightmost buttons:
  
  Allow one to respectively import Turing Machines you've already created as building blocks, and allow you to set up transitions between Turing Machines.

JFLAP Example

• For example, earlier today we built a machine in JFLAP that converts strings over `a`'s and `b`'s into one over just `b`'s.
• It finishes with the tape head on the rightmost symbol.
• We can combine this machine with a machine to rewind the tape to finish with the tape head on the leftmost symbol:
  

The Church-Turing Thesis

• This thesis is that any computational process that can be effectively carried out on a real-world computational device can be simulated by a Turing Machine.
• It was first called "Church's Thesis" by Kleene, "Recursive Predicates and Quantifiers," Trans. of the AMS. Vol. 53. No. 1. 1943.
• Since you can always come up with new computational devices, it is not something you can prove.
• However, so far no one since it was proposed in the 1940s has come up with a model which is both physically implementable which cannot be simulated by a Turing Machine.
• Over the next week, we will look at some of the models that have been considered.
• These include: multi-tape variants of Turing Machines, multi-stack PDAs, RAMs (computers with machine code instructions), cellular automata, lambda calculus (based on functional programming approaches like in LISP or scheme), rewrite systems, classical and quantum physics based processes, etc.