Outline

• Pumping Lemma
• Context-free Grammars
• In-Class Exercise
• Formal Definitions
• Examples / Designing
• Parsing

The Pumping Lemma

• At the end of last day, we introduced the Pumping Lemma. Let's refresh our memory on the inntuition for this lemma before giving some examples of its use.
• Suppose we have a machine `M` with `k` states. Feed in some input string `w` of length `n>k`. At some point in the computation, by the pigeonhole principle, the machine must repeat a state.
• Suppose `M` accepts `w`. Then we can imagine `M`'s computation splitting `w` into 3 pieces, `w=xyz`, according to the diagram:
  

More on the Pumping Lemma

• But this implies that `M` accepts the strings `xz`, `xyyz`, `xyyyz`, etc.
• We have thus established the Pumping Lemma:
  Lemma (Pumping Lemma). If `A` is a regular language, then there is a number `p` (the pumping length) where, if `s` is any string in `A` of length at least `p`, then `s` may be divided into three pieces `s=xyz`, such that: for each `i geq 0`, `xy^iz` is in `A` for `|y| > 0`, and `|xy| leq p`.
• The pumping lemma first appeared in Bar-Hillel, Perles, and Shamir. "On formal properties of simple phrase structure grammars," Z. Phonetik. Sprachwiss. Kommunikationsforsh. Vol 14. (1961). pp.143--172.

Using the Pumping Lemma

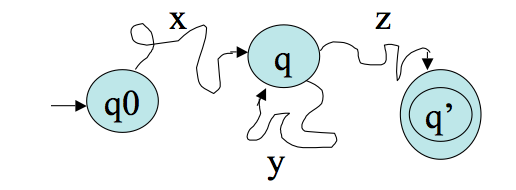
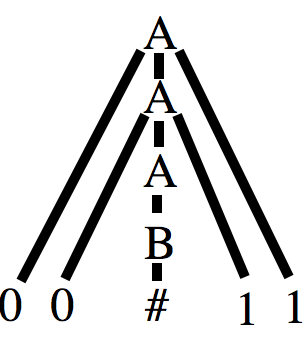
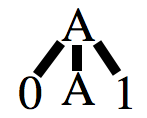
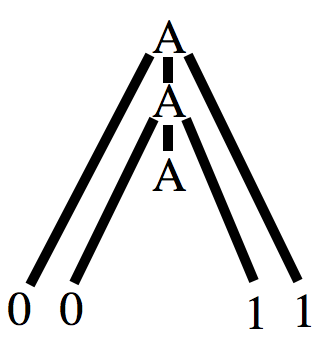
We can use the pumping lemma to show there are languages that are not regular. For example, let `C={ w| w \ mbox(has an equal number of 0's and 1's)}`. To prove `C` is not regular:

• Suppose DFA `M` that recognizes `C`.
• Consider the string `w = 0^p1^p`. This string is in the language and has length greater than `p`.
• So by the pumping lemma `w = xyz`, where `|xy| leq p`, `|y| > 0`, and where `xy^iz` is in the language for all `i geq 0`. That means `x = 0^k` and `y=0^j` where `k+j leq p` and `j>0`. But then taking `i=0`, `xz = 0^(p-j)1^p` should be in `C`. As `p-j` is not equal to `p` this give a contradiction. So `C` is not regular.

More Examples

• Show `L = {ww^R | w in Sigma^star}` is not regular.
  • Suppose `M` is a DFA that recognizes `L`.
  • Let `p` be `M`'s pumping length
  • Consider the string `w = 0^p110^p`. This string is in the language and has length greater than `p`.
  • So by the pumping lemma `w = xyz`, where `|xy| leq p`, `|y|> 0`, and where `xy^iz` is in the language for all `i geq 0`. That means `x = 0^k` and `y=0^j` where `k+j leq p` and `j>0`. But then taking `i=0`, `xz = 0^(p-j)110^p` should be in `L`. The two `11`'s not occur on the left hand half of `xz` and there are no `1`'s on the right hand half. So `xz` is not of the form string followed by reverse of the same string so in not in `L`, contradicting the pumping lemma. So L is not regular.
• Show that `L = {w in Sigma^star | \ n_a(w) < n_b(w) }` is not regular. Here `n_x(w)` denotes the number of occurrences of alphabet symbol `x` in `w`.
  • Suppose `M` is a DFA that recognizes `L`.
  • Let `p` be `M`'s pumping length
  • Consider the string `w = a^pb^(p+1)`. This string is in the language and has length greater than `p`.
  • So by the pumping lemma `w = xyz`, where `|xy| leq p`, `|y| > 0`, and where `xy^iz` is in the language for all `i geq 0`. That means `x = a^k` and `y=a^j` where `k+j leq p` and `j>0`. But then taking `i=2`, `xy^2z = a^(p+j)b^(p+1)` should be in `L`. As `j>0`, `n_a(xy^2z) = p+j` is not less than `n_b(xy^2z )= p+1`. So `xy^2z` is not in `L`, contradicting the pumping lemma. So `L` is not regular.

In-Class Exercise

Let `k: NN -> NN` be a function such that `k(n) > n`. We know by the surjective pigeonhole principle that any function from `f:{0,1}^n -> {0,1}^{k(n)}` where `k(n) > n` must miss some point in `{0,1}^{k(n)}` (i.e., is not onto). Suppose `f:{0,1}^{\star} -> {0,1}^{\star}` maps string of length `n` to one's of length `k(n)`. Such a function `f` is a hard with respect to a class of adversary languages `mathcal{A}` and stretch `k` if there is no `A in mathcal{A}` such that for all `n` and for all `y in {0,1}^{k(n)}`, `y in A` iff there is an `x in {0,1}^n` such that `f(x) = y`. Such an `f` is a pseudo-random number generator with respect to `mathcal{A}` if the odds an `A in mathcal{A}` guesses which strings of length `k(n)` are in the image of `f` cannot be bounded away from a half. In cryptography, one might study techniques for converting hard functions into pseudo random ones.

Consider the function `f:{0, 1}^\star -> {0, 1}^\star` which maps strings `w=w_0... w_n` to `w' = w_0... w_nz` where `z` has the same value as `w_{lfloor n/2 rfloor}`. To make this function defined for all strings we define `f(epsilon) = 1`. Show this function is hard with respect to adversaries which are regular languages.

Post your solution to the Mar 4 In-Class Exercise Thread.

Using the Myhill Nerode Theorem to Show a Language is not Regular

• Recall the Myhill Nerode Theorem says: A language is regular iff the set of equivalence classes of L with respect to indistinguishability is finite.
• Consider the language `L={0^{2^i}| i \geq 0}`. This is a unary language, so it would be hard to use the pumping lemma to show it is not regular.
• On the other we can see for each `i ne j`, the string `0^{2^i}` is distinguishable from `0^{2^j}`. This is because if we add concatenate `0^{2^i}` to itself we get
  `0^{2^i}0^{2^i} = 0^{2^{i}+2^{i}} = 0^{2\cdot 2^{i}}= 0^{2^{i+1}}`
  which is in the language, but `0^{2^j}0^{2^i} = 0^{2^{j}+2^{i}}` is not in the language for any other `j`. So `[0^{2^i}]_L ne [0^{2^j}]_L` for all `i ne j `.
• So the number of equivalence classes of `L` with respect to distinguishability is not finite. So `L` is not regular by the Myhill Nerode Theorem.

Context Free Languages

• We saw that regular languages were useful for doing things like string matching.
• This might occur in practice as the so-called lexical analysis phase of compiler. That is, the phase in which we recognize tokens like language reserved words, variable names, constants, etc.
• We now turn to ways of specify programming languages or even aspects of natural languages.
• The key to this is to have some way to recognize the underlying structures such as nouns and verbs, or control blocks, etc of the language.
• Context Free Grammars (CFGs), which are a less restricted form of grammar than a regular grammar, and their languages will provide us with the tools to do this.

Example CFG

• Recall a grammar consists of a collection of substitution rules (aka productions). For instance: `A -> 0A1`, `A -> B`, `B -> #`
• Usually, we'll write variables using uppercase letters or in brackets like `<mbox(variable)>`. Terminals are supposed to be strings over the alphabet of the language we are considering.
• In a CFG, the left hand side of each rule has one variable; the right hand side can be a string of variables and terminals.
• Variables can be substituted for; terminals cannot. One variable denoted by S is usually distinguished as a start variable.
• An example sequence of substitutions (aka a derivation) in the above grammar might be: `A => 0A1 => 00A11 => 00B11 => 00#11`

More on CFGs

• Such a derivation might also be drawn as a parse tree:
  
• Here the derivation `A => 0A1` gives the tree portion:
  
• `A => 0A1 => 00A11` gives
  

Formal Definitions

• A context free grammar is a 4-tuple `(V, Sigma, R, S)` where:
  1. `V` is a finite set called the variables.
  2. `Sigma` is a finite set, disjoint from `V` called the terminals.
  3. `R` is a finite set of rules. Here each rule being a pair consisting of a variable and a string of variables and terminals.
  4. `S in V` is a start variable.
• For a rule `A -> w` where `w` is a string over `(V cup Sigma)`, and for other strings `u` and `v`, we say uAv yields uwv, written `uAv => uwv`. We say `u` derives `v`, written `u=>^star v`, if there is a finite sequence: `u => u_1 => u_2 => ... => u_k=> v`.
• The language of a CFG is the set of strings over `Sigma^star` derivable from its start symbol.
• A language given by a context-free grammar (CFG) is called a context-free language (CFL -- aka Canadian Football League).
• Sometimes we abbreviate multiple rules with same left hand side using a `|`. For example, `A -> 0A1 | B` .
• Context-free grammars were first defined by Chomsky, N. "Three Models for the Description of Language," I R E Trans. on Information Theory. Vol. 2. Iss. 3. 1956. pp. 113--124.
• Backus (1959) and Naur (1960) later developed a notation for CFG which is often used in the context of computer languages (so-called Backus-Naur form).

Example

• Consider the grammar `G= (V, Sigma, R, <EXPR>)` where `V` is `{<EXPR>, <TERM>, <FACTOR>}` and `Sigma` is `{a, +, times, (, )}` and the rules are: `<EXPR> -> <EXPR> + <TERM> | <TERM>`, `<TERM> -> <TERM> times <FACTOR> | <FACTOR>`, and `<FACTOR> -> (<EXPR>) | a`.
• One can verify that `<EXPR> =>^star (a+a) times a`.
• This is true since `<EXPR> =><TERM> =><TERM> times <FACTOR>`
  `=><FACTOR> times <FACTOR> =>(<EXPR>) times <FACTOR>`
  `=>(<EXPR> + <TERM>)times <FACTOR> =>(<TERM>+<TERM>) times <FACTOR>`
  `=>(<FACTOR> + <TERM>) times <FACTOR> =>(a+ <TERM>) times <FACTOR>`
  `=>(a+ <FACTOR> ) times <FACTOR> =>(a+a) times <FACTOR> =>(a+a) times a`