Outline
- Star Height
- Homomorphism and Quotients
- Quiz
- Algorithms for Regular Languages
- Pumping Lemma
Introduction
- Last week, we were talking about different equivalent ways to classify the regular languages.
- So far we have shown the regular languages can be defined equivalently as those languages given by:
- DFA
- NFA
- Regular Expression
- Left-Linear or Right-linear grammars
- We said regular expressions are a convenient notation for specifying languages, and we have good algorithms to convert regular expression to NFAs and somewhat less efficient algorithms to convert these DFAs.
- Finally, we have given linear time constant space algorithms for checking if a string is accepted by a DFA.
- Today, we begin by looking at a way to classify how hard a regular expression is before we move on to talk some more about additional closure properties of the regular langugaes and string algorithms.
- Finally, we show their exists some languages not recognized by DFAs.
Classifying Regular Languages
- Besides giving a convenient format for describing a regular language, regular expressions can also be used to measure how hard a regular language is.
- If you think about our proof that NFAs can simulate each of the regular operations, only simulation of Kleene Star involved creating loops in the automata graph. So it natural to estimate "how complex" an automata is by counting nestings of Kleene Star.
- We define the star-height of a regular expression inductively. If `R` is `emptyset`, `epsilon` or an alphabet symbol `mbox(star)(R) := 0`. Given regular expressions `R_1` and `R_2`, `mbox(star)((R_1 cup R_2)) = mbox(star)((R_1R_2)) := \max(mbox(star)(R_1),mbox(star)(R_2))` and `mbox(star)(R_1^\star) := mbox(star)(R_1) + 1`.
- Hence, given a regular expression `R` there is a simple recursive algorithm to compute its star-height. On the other hand it is unclear whether one couldn't find an `R'` with the same language of smaller star-height.
Facts about Star-height
- Eggan (1963) showed that there are languages which require arbitrarily large star-height. (For example, strings over `{a,b}` such that the number of `a`'s is congruent to the number of `b` mod `2^{n-1}` requires star-height `n`)
- Kirsten (2005) gives a double exponential-space algorithm for computing the minimal star-height of a language.
- Languages of star-height 0 have an abstract algebra characterization in terms of so-called aperiodic syntactic monoids, Schutzenberg (1965). Here aperiodic just means they don't contain a non-trivial proper syntactic monoid.
-
For higher star-height, there are notions like locally testable, and piecewise testable expressions, which have characterizations in terms of pseudo-varieties of monoids (Eilenberg).
- A generalized regular expression is defined the same way as a regular expression but we also allow `cap`. This doesn't effect the class of languages since one can show that the regular language are closed under intersection via a Cartesian product construction.
- It is open whether star-height greater than 1 is needed for generalized regular expressions.
Quiz
Which of the following is true?
- The construction from class of an NFA from a regular expression of length `m` produces an NFA with `O(m)` states.
- `((ab)^{\star}\cap(a\cup b)^{\star))` is a regular expression.
- Our proof that the language of any DFA is the language of a regular expression was a proof by contradiction.
Introduction to Homomorphisms
- From time to time it is useful to be able to translate things from one language to another.
- In the simplest case this might involve transliterating character by character, as when we convert Russian spellings of proper names into English. For example, Сталин -> STALIN.
- As another example, we might want to encode our alphabet using an error correcting code.
- In converting from one such language to another we have to be sensitive to the fact that sometimes an exactly equivalent string might not exist. For example, in English we have the words blue and turquoise which in some other language might both be translate to blue.
- Homomorphisms allow us to do these kind of mappings for regular languages.
Definition of Homomorphism
- Given two alphabets `Sigma` and `Sigma'`. A function `h:Sigma ->(Sigma')^star` is called a homomorphism. The domain of `h` can be extended to all strings over `Sigma^star` as follows: if `w=a_1a_2 ldots a_n` then `h(w) = h(a_1)h(a_2) ldots h(a_n)`.
- Given a language `L`, its homomorphic image is defined to be `h(L) = {h(w)| w in L}`.
- For example strings over `{a,b}` might be encoded to strings over `{0,1}` via the homomorphism: `h(a) = 000`, `h(b) = 111`.
- In this case the language `L={aa, baba}` has as its homomorphic image: `h(L) = {000000, 111000111000}`.
- A homomorphism does not have to be one to one. One could map `{a, b}` to the alphabet `{a}` via `h(a)=a`, `h(b) =a`. In which case `h(ababa) = aaaaa`.
Closure under Homomorphism
Theorem. Let `L` be a regular language over `Sigma` and let `h:Sigma ->(Sigma')^star` be a homomorphism. Then `h(L)` is a regular language over `Sigma'`.
Proof. We have shown that every regular language can be represented by a regular expression. Let `R` be the regular expression for `L`. We prove by induction on the complexity of `R` that `h(L)` will be regular. In the base `R` is either a symbol a of `Sigma` or it is the empty string, or it is the empty set. In the latter two cases `L(R) = L(h(R))`, so we are done. In the first case, we note that `h(a)` is a string over `Sigma'` and so will be a regular expression over the `Sigma'` alphabet. for the induction step, `R` is
either of the form `R = (R_1R_2)`, `R = (R_1 cup R_2)`, or `R = (R_1)^star`. In each of these cases, we have by the induction hypothesis a regular expressions `R_1'` and `R_2'` for the homomorphic images of the languages of the subexpressions. So to make regular expressions for the homomorphic
image of the language for `R` we can take either: `R' = (R_1'R_2')`, `R' = (R_1' cup R_2')`, or `R' = (R_1')^star`.
A generalization of closure under homomorphism, closure under substitutions, was first proven in Bar-Hillel, Perles, and Shamir 1961.
Quotients
- A common problem in the computer processing of natural languages is to come up with stems of a given sequence of words.
- For example, if we do a search engine search on fished, fishing, fishes, etc. as a preprocessing step this might be stemmed to just the word 'fish'.
- We will next consider a notion of the quotient of two languages which allows us to formally consider things like stemming.
Definition. If `A` and `B` are two languages, their quotient `A/B` is the language: `{v | vw in A \ mbox(and)\ w in B}`.
- So if `A={mbox(fished, fish, fishes, fishing, jumping, oranges)}` and `B={mbox(ing, ed)}` then `A/B = {mbox(fish, jump)}`.
Closure under Quotients
Theorem. If `A` and `B` are regular languages, then `A/B` is also a regular language.
Proof. Let `M=(Q, Sigma, delta, q_0, F)` be a DFA for `A` and let `M'` be a DFA for `B`. So a string `v` is in `A/B = (L(M))/(L(M'))` if `delta^star(q_0,v)=q_i` for some `i`, `delta^star(q_i,w) in F`, and `w in L(M')`. Let `M_i = (Q, Sigma, \delta, q_i, F)` , then `L(M_i) cap L(M')` is regular by a cartesian product construction. Notice `L(M_i) cap L(M')` is nonempty iff the two conditions `delta^star(q_i, w) in F`, and `w in L(M')` hold for some `w`. Further, we can check if `L(M_i) cap L(M')` is nonempty by seeing if some accepting state of this language is reachable from the start state. Hence, we can make a machine for `A/B` as `(Q, Sigma, delta, q_0, F')` where `F'` are those state in `Q` such that `L(M_i) cap L(M')` is nonempty.
This result is due to Ginsberg and Spanier 1963.
Membership, Emptiness and Finiteness Checking
Theorem. Given a regular language `L` in standard representation and a
string `w`, there are algorithms which can check: (a) if `w` is in `L`, (b) if `L` is empty, and (c) if `L` is finite.
Proof. The first step of each algorithm is to obtain a DFA for L. For (a) we can just use the Java program (modified
with the correct transition table) we wrote a few
lectures back to simulate a DFA on a input string. For (b), we view the transition function of the finite automata for `L`
as specifying a labeled graph and we use the algorithm we gave earlier for reachability in a graph to check if an accept state is
reachable from the start state. If it is, following the edge labels would give an element in `L` and so would mean `L` was non-empty.
If no accept state was reachable, the language would be empty. For (c), let `M = (Q, Sigma, delta, s, F)` be a DFA for `L` .
An algorithm to check if `L` is finite could cycle through each state `q` of `Q` and check if `q` is reachable from `s`. If it is
it then check is `q` reachable from `q`. If it is, it finally checks whether any accepting state is reachable from`q`. If any
`q` meets all three of these conditions then by cycling over the `q` to `q` path differing numbers of times we can show arbitrarily many
strings are in the language. This is because `M` is a DFA so the loop must involve traversing some alphabet letters. So the language will not be finite. If no such `q` exists then we know that no accept state is reachable
from any state associated with a cycle so the language must be finite.
The above Theorem is due to Moore (1956).
Remark. Suppose our regular language was presented as a regular expression `R`. The way we have been suggesting to perform check if `w` is in `L`
is to convert `R` to an NFA `N`, do the powerset construction to get a DFA `D`, minimize the DFA, run the algorithm on the DFA. If `N` has `m` states then the size of D might be as large as `O(2^m)` which might mean a lot of space is used even after minimization. To see this consider the language {`w \in {0,1}^star`| the `m`th last character of `w` is a `0`}. This has an `m` state NFA but requires `Omega(2^m)` states as a DFA. For this reason, people often try to simulate `w` directly on the NFA, keeping a list of states which one might be in at an given step.
That is, suppose CurrentStates is a list of states we might be in after processing the first `t` characters from a string `w`. Let `w_{t+1}` be the `t+1`st character of `w`. Initial NextStates to be the empty set of states. Then for each state `q` in CurrentStates, we use our NFAs transition `delta`, and add the states `E(delta(q, w_{t+1}))` to NextStates. Once we have done this for all states in CurrentStates. We set CurrentStates = NextStates and proceed to the next character. If after processing the whole string our last set of CurrentStates has an accept state in it we accept, otherwise, we reject.
One can verify the runtime of this algorithm is `O(m cdot |w|)` and it uses at most `O(m log m)` space.
Remark. For some particular regular expressions, rather than use an NFA, we can just use a DFA. For example, if we have a regex only involving concatenation and alphabet symbols of length `n` (corresponding to searching for a pattern like "chris" within a string), then we can make a DFA with n+1 states with appropriate back arrows. If we have a pattern of star height 0, we can use the distributive property of regex's to rewrite this as a union of fixed strings. For example, `(a cup b)(a cup b)` becomes `(aa\cup ab \cup ba\cup \b\b)`. If we simulate an NFA on each of the union'd strings, we only have to keep track of states proportional to the number of unions rather than the number of symbols in the regex.
The question of minimizing regular expressions for finite languages is an active area of research as evidenced by Gruber , Holzer, Wolfsteiner 2020 results on the time complexity of approximating the smallest regular expression for a finite language.
The Pumping Lemma
- Suppose we have a machine `M` with `k` states. Feed in some input string `w` of length `n>k`. At some point in the computation, by the pigeonhole principle, the machine must repeat a state.
- Suppose `M` accepts `w`. Then we can imagine `M`'s
computation splitting `w` into 3 pieces, `w=xyz`,
according to the diagram:
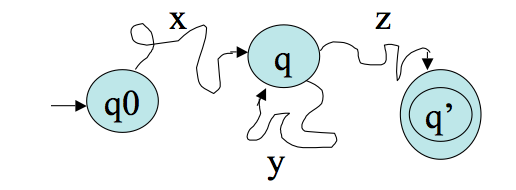
More on the Pumping Lemma
- But this implies that `M` accepts the strings `xz`, `xyyz`, `xyyyz`, etc.
- We have thus established the Pumping Lemma:
Lemma (Pumping Lemma). If `A` is a regular language, then
there is a number `p` (the pumping length) where, if `s` is any string in `A` of length at least `p`,
then `s` may be divided into three pieces `s=xyz`, such that: for each `i geq 0`, `xy^iz` is in `A` for `|y| > 0`, and
`|xy| leq p`.
- The pumping lemma first appeared in Bar-Hillel, Perles, and Shamir. "On formal properties of simple phrase structure grammars," Z. Phonetik. Sprachwiss. Kommunikationsforsh. Vol 14. (1961). pp.143--172.
Using the Pumping Lemma
We can use the pumping lemma to show language are not regular.
For example, let `C={ w| w \ mbox(has an equal number of 0's and 1's)}`. To prove `C` is not regular:
- Suppose DFA `M` that recognizes `C`.
- Consider the string `w = 0^p1^p`. This string is in the language and has length greater than `p`.
- So by the pumping lemma `w = xyz`, where `|xy| leq p`, `|y| > 0`, and where `xy^iz`
is in the language for all `i geq 0`. That means `x = 0^k` and `y=0^j` where `k+j leq p` and `j>0`. But then taking `i=0`,
`xz = 0^(p-j)1^p` should be in `C`. As `p-j` is not equal to `p` this give a contradiction. So `C` is not regular.
More Examples
- Show `L = {ww^R | w in Sigma^star}` is not regular.
- Suppose `M` is a DFA that recognizes `L`.
- Let `p` be `M`'s pumping length
- Consider the string `w = 0^p110^p`. This string is in the language and has length greater than `p`.
- So by the pumping lemma `w = xyz`, where `|xy| leq p`, `|y|> 0`, and where `xy^iz`
is in the language for all `i geq 0`. That means `x = 0^k` and `y=0^j` where `k+j leq p` and `j>0`.
But then taking `i=0`, `xz = 0^(p-j)110^p` should be in `L`. The two `11`'s not occur on the
left hand half of `xz` and there are no `1`'s on the right hand half. So `xz` is not of the form string followed by reverse of the same string so in not in `L`, contradicting the pumping lemma. So L is not regular.
- Show that `L = {w in Sigma^star | \ n_a(w) < n_b(w) }` is not regular. Here `n_x(w)` denotes the number of occurrences of alphabet symbol `x` in `w`.
- Suppose `M` is a DFA that recognizes `L`.
- Let `p` be `M`'s pumping length
- Consider the string `w = a^pb^(p+1)`. This string is in the language and has length greater than `p`.
- So by the pumping lemma `w = xyz`, where `|xy| leq p`, `|y| > 0`, and where `xy^iz`
is in the language for all `i geq 0`. That means `x = a^k` and `y=a^j` where `k+j leq p` and `j>0`.
But then taking `i=2`, `xy^2z = a^(p+j)b^(p+1)` should be in `L`. As `j>0`, `n_a(xy^2z) = p+j` is not
less than `n_b(xy^2z )= p+1`. So `xy^2z` is not in `L`, contradicting the pumping lemma. So `L` is not regular.






















