Outline

• Regular Languages and Regular Expressions
• Quiz
• Regular Grammars
• Classifying Regular Languages

Regular Expressions

• At the end of last day, we briefly introduced regular expressions. Let me now give a quick refresher before starting new stuff.
• In arithmetic, we can use the operations `+` and `cdot` to build up expressions such as: `(5 + 3) cdot 4`.
• Similarly we can use the regular operations to build up expressions describing regular languages.
• For instance, `0(0 cup 1)^star`.
• This means the language which results from concatenating the language containing 0 with the language of `(0 cup 1)^star`. This in turn is the star of the union of the two languages one containing just `0`; the other containing just `1`.
• These kind of expressions are used in many modern programming languages: Perl, PHP, Python, Java, AWK, GREP.

Formal Definition of a Regular Expression

We say that `R` is a regular expression if `R` over some alphabet `Sigma` is:

1. `a` for some symbol `a` in the alphabet `Sigma`.
2. `epsilon`.
3. `emptyset`.
4. `(R_1 cup R_2)` where `R_1` and `R_2` are regular expressions. `R_1 + R_2` is used by JFLAP, most programming languages use `(R1 | R2)`.
5. `(R_1R_2)` where `R_1` and `R_2` are regular expressions.
6. `(R_1)^star` where `R_1` is a regular expression.

We write `R^+` as a shorthand for `R\ R^star`. Notice also we tend to be lazy on parentheses even thought to be fully well-formed everything has to be completely parenthesized.

We write `L(R)` for the language given by the regular expression.

Regular expressions were first considered in Kleene (1956).

In older books, you sometimes see regular expressions called rational expressions.

Examples of the Definition

• `0^star10^star={w| w \ mbox{contains a single} \ 1}`
• `(01 cup 10) = {01, 10}`
• `((0 cup 1) (0 cup 1))^star = {w| w \ mbox{is of even length}}`
• `(epsilon cup 0)(epsilon cup 1)= {epsilon ,0,1,01}`
• `1^star emptyset = emptyset`
• `emptyset^star = {epsilon}`

In a programming language like say PHP or Perl you might use things like: "\.|\,|\:|\;|\"|\'|\`|\]|\[|\{|\}|\(|\)|\!|\||\&" to match against, for instance, the punctuation symbols you want.

If you want to see regular expressions gone wild check out the Perl solution to the 99 bottles of beer song.

Some Regular Expression Identities

The following identities (`equiv` here meaning have the same language) are not too hard to verify:

• `(R cup R) equiv (emptyset cup R) equiv (R cup emptyset) equiv (epsilon R) equiv (R epsilon) equiv R`.
• `(R cup S) equiv (S cup R)`
• `R(S cup T) equiv (RS cup RT)` and `(S cup T)R equiv (SR cup TR)`.
• `R(ST) equiv (RS)T`
• `(R cup S)^\star equiv (R^\star S)^\star R^\star`
• `(R S)^\star equiv \epsilon \cup R(S R)^\star S`
• For any `n ge 1`, `R^\star equiv (epsilon cup R cup R^2 cup ... cup R^(n-1))(R^n)^\star`

Viewing emptyset as `0`, empty string as `1`, concatenation as multiplication, union as plus, the above show the regular expressions are a so-called semi-ring, and perhaps motivates why they are sometimes called rational expressions. It is not a ring because given `R` we can't easily define a regular expression `R'` such that `R cup R' equiv emptyset`.

Semi-rings don't typically have a star operation (there is a something called a star semi-ring). To reduce to the situation where one can get rid of star, one can look at languages which have the finite power property. That is, languages for which `L^\star = epsilon cup L cup ... cup L^(n-1)` for some `n ge 1`. Algorithms for checking this property have been given by Hashiguchi and Simon.

Quiz

Which of the following is true?

1. A DFA defined using our five tuple notation for DFAs is an NFA defined using our five tuple notation for NFAs without any modification.
2. If two states in a DFA are indistinguishable with respect to the extended transition function, then they will be combined in our DFA minimization procedure.
3. The automata derived from the syntactic monoid of a language as we did last day is always a DFA.

Equivalence with Finite Automata

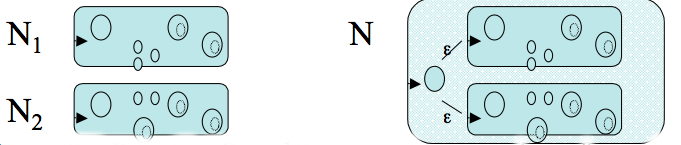
• We want to show that a language is regular if and only if some regular expression describes it.
• We will do this in two steps:
  • Prove if a language is described by a regular expression, then it is regular
  • Prove if a language is regular, then it is described by a regular expression.

Proof that regular expression implies regular

• The proof is by induction on the complexity (number of uses of union, `star`, or concatenation) of the regular expression. In the base case, we have regular expressions which make no use of union, `star`, or concatenation.
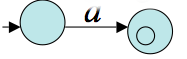
  1. Let `R = a` for some `a` in `Sigma`. Then the following NFA recognizes the languages contain only a:
     
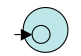
  2. Let `R = epsilon`. Then the following NFA recognizes it:
     
  3. Let `R = emptyset`. Then the following NFA recognizes it:
     

Proof cont'd

Assume now the result holds for languages for which the total number of uses of union, `\star`, or concatenation is at most `n`. Consider `R` a regular language of complexity `n+1`. There are three cases to consider:

1. `R` is of the form `(R_1 cup R_2)` where `R_1` and `R_2` are regular expressions of complexity `leq n`. By induction let `N_1` and `N_2` be the machines for `R_1` and `R_2`. Define `N` for `R` as:
   
   Roughly, we make a new machine that has a copy of each of the two machines `N_1` and `N_2` together with a new start state for the overall machine. From this new start state we have two `epsilon` transitions: one to what had been the start state of `N_1` and one to what had been the start state of `N_2`.
2. `(R_1R_2)` where `R_1` and `R_2` are regular expressions of complexity `leq n`. By induction let `N_1` and `N_2` be the machines for `R_1` and `R_2`. Define `N` for `R` as:
   
   The idea is we make a new machine with copies of `N_1`, `N_2`. In this new machine the start state will be the start state of the copy of `N_1`. The `N_1` copy will no longer have accept states; however, we will have an `epsilon` transistiton from each former accept state of `N_1` to a what had been the start state of `N_2`.
3. `(R_1)^star` where `R_1` is a regular expression of complexity `leq n`. By induction let `N_1` be the machine for `R_1`. Define `N` for `R` as:
   
   That is, we make a new machine `N` which consists of a new start state that is accepting. From this, we add an `epsilon` transition to what had been the start state of a copy of `N_1`. For each accept state in this `N_1` copy, we add an `epsilon` transition back to what had been the start state of `N_1`.