Outline

• Nondeterministic Finite Automata
• Equivalence of DFAs and NFAs
• Quiz
• State Minimization

Nondeterministic Finite Automata

• We begin today by looking at a second abstract machine model for representing single-pass, constant memory, string algorithms.
• One problem with DFAs is that, as we've seen, a simple construction like taking the union of two languages, results in a machine with the product of the two sub-machines number of states.
• So if even we had a progamming language with 50 distinct kinds of syntactic units and keywords, each of which are recognizable each by a small machine of say 4 states, then a machine to recognize any of the union of these keywords would have `4^{50}=2^{100}` states -- not really practical.
• This issue boils down to that having trap states, and transitions, in general, for every alphabet symbol, can make one's diagrams messy, painful to maintain, and huge.
• To get around this one could imagine using a rule which says a string is automatically rejected if it ever happens that one cannot transition out of a state by reading the next symbol of the string.
• It is also sometimes convenient if we want to build bigger automata out of smaller automata, to allow two transitions with the same alphabet symbol out of a state. Or even to allow transitions where we don't read a symbol at all!
• These ideas motivate the concept of nondeterministic machine.

Example NFA

• Notice we have more than one transition out of a state, we can have `epsilon`-transitions, and we don't need to have a transition from every alphabet symbol from a state.
• We say the NFA accepts `w` roughly if there is some sequence of transitions beginning with the start state, that processes each character of w, and ends in an accept state.
• For instance, the machine above accept `\epsilon`, `0`, `00`, `000`, `1`; but rejects `01`, `11`, `0001`. It rejects `01` because although it can get to state `q_2` after seeing `epsilon 0 = 0`, it has nowhere to go when it sees a `1` so it can't process the `1` so it rejects. No other path in the machine processes `01` even this far.

Formal Definition of an NFA

• Recall the power set of a set `Q`, `P(Q)`, is the set of all subsets of `Q`.
• A nondeterministic finite automaton is a 5-tuple `(Q, Sigma, delta, q_0, F)` where:
  1. `Q` is a finite set of states
  2. `Sigma` is an alphabet
  3. `delta: Q times Sigma cup {epsilon} rightarrow P(Q)` is the transition function
  4. `q_0 in Q` is the start state
  5. `F subseteq Q` is the set of accept states.
• NFAs were proposed in a paper of Rabin and Scott in 1959. (IBM J. Research and Development. Vol. 3 Iss. 2)

Example

• The machine a couple slides back is defined as `(Q, Sigma, delta, q_1, F)` where:
  1. `Q={q_1, q_2, q_3}`
  2. `Sigma={0,1}`
  3. `delta` is given by:
     `delta(q_1, epsilon)rightarrow {q_2} quad delta(q_1, 0)rightarrow {} quad delta(q_1, 1) rightarrow {q_2,q_3}`
     `delta(q_2, epsilon)rightarrow {} quad delta(q_2, 0)rightarrow {q_2} quad delta(q_2, 1)rightarrow {}`
     `delta(q_3, epsilon)rightarrow {} quad delta(q_3, 0)rightarrow {} quad delta(q_3, 1)rightarrow {}`
  4. `q_1` is the start state
  5. `F = {q_2, q_3}`

Formal Definition of Accepts

• To define what it means for an NFA to accept we can modify the definition of `delta^star` so that it works on a set of states. i.e., `delta^star(q_i, w) =Q_j`, where `Q_j` is the set of possible states one could be in after processing `w` starting in state `q_i`.
• We say `M` accepts `w` then if `delta^star(q_0, w) cap F` is nonempty.
• We write `L(M)` for the set of strings `M` accepts.

Equivalence of NFAs and DFAs -- The Power Set Construction

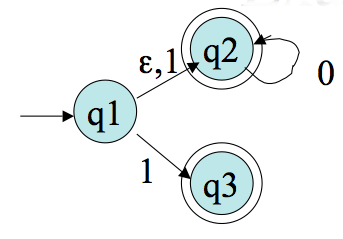
Theorem Any language recognized by an NFA is recognized by some DFA.

Proof: Given an NFA `N= (Q, Sigma, delta, q_0, F)` we want to simulate how it acts on a string `w` with a DFA, `M= (Q', Sigma, delta', q_0', F')`. The idea is we want to keep track of what possible states it could be in after reading the first `m` characters of `w`. Let `Q'= P(Q)`, the power set of `Q`. The alphabet is the same. For each `R in Q'` (i.e., `R subseteq Q`) and `a in Sigma`, let `delta'(R, a) = {q in Q | q in E(delta(r,a)) \ mbox{for some} \ r in R}`. Here `E(q')` is the set of states reachable from `q'` following 0 or more `epsilon` transitions, for a set of states `Q''`, `E(Q'')` is the union of `E(q'')` for `q'' in Q''`. Let the new start state be `q_0'=E(q_0)`. Let `F' = {R in Q'| R \ mbox{contains an accept state of} \ N}`.

This construction is from the original NFA paper of Rabin and Scott (1959).

Example Conversion

• Here is an initial NFA:
  
• Here is the result of the conversion, where unreachable states have been removed:
  
• JFLAP let's you step through the conversion process
• The subscript beneath a state after the conversion corresponds to a set of states from the original NFA
• Notice what JFLAP gives you actually is still an NFA. What's missing in the above is a transition from the state {q_2} to a trap state {} on either a 0 or a 1.

Quiz

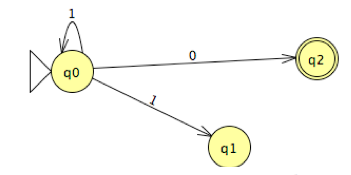
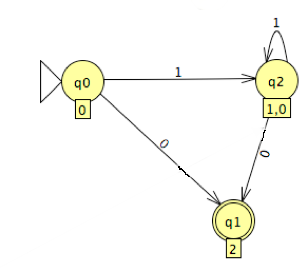
Which of the following is true?

1. The state set of a DFA is allowed to be infinite.
2. All transitions starting from a trap state map to the trap state.
3. Our proof that regular languages are closed under union directly used the pigeonhole principle.

State Minimization

• We say two states `p`, `q` of a DFA `M` are indistinguishable if `delta^star(p,w) in F` implies `delta^star(q,w) in F` and `delta^star(p,w) !in F` implies `delta^star(q,w) !in F`.
• Otherwise, `p`, `q` are said to be distinguishable.
• Let `p~_I q`,if `p` and `q` are indistinguishable. Notice this is an equivalence relation.
• We now present an algorithm to find the minimal DFA equivalent to `M`.
• The idea is to first compute the equivalence classes of the indistinguishable equivalence relation. Then make one state for each equivalence class, and make an appropriate new transition function.

Procedure for Equivalence

1. Remove all inaccessible states. This can be done by checking for each state if there is a simple path from the start state to it.
2. Consider all pairs `(p,q)` of states. If `p in F` but `q !in F` or vice versa, then mark the pair `(p,q)` distinguishable.
3. Repeat until no previously unmarked pairs are marked:
   1. For all pairs `(p,q)` and all `a in Sigma`, compute `delta(p,a) = p_a` and `delta(q,a) = q_a`. If the pair `(p_a,q_a)` is marked as distinguishable, mark `(p,q)` as distinguishable. Idea: if in `p` `q` on the same letter you transition to distinguishable states then `p` and `q` must be distinguishable.

Procedure to Build Minimal Automaton

1. Use procedure of last slide to generate state equivalence classes for original automata.
2. For each equivalence class `[p] = {q | p~_I q}` create a new state.
3. For each transition rule `delta(r,a)=s` of the original machine, add a transition `delta([r],a)=[s]`.
4. The initial state of the new machine is `[q_0]` where `q_0` was the state of the machine we are trying to minimize.
5. The final states of the new machine is the set `{[f] | f in F}`.

The first procedure for minimizing finite automata was given in Huffman 1954 (J. Franklin Institute. Vol 257. Iss. 3-4).

Our procedure above probably runs in quadratic time, the best known algorithm is `O(n log n)` due to Hopcroft 1971.