










Designing DFAs - Product Construction
CS154
Chris Pollett
Feb. 12, 2020











CS154
Chris Pollett
Feb. 12, 2020
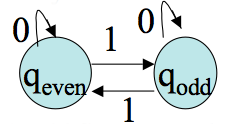
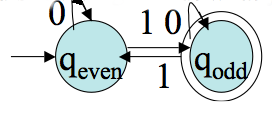
Let `M= (Q, Sigma, delta, q_0, F)` be a DFA, and `G_M` be its associated transition graph. Then for every `q_i`, `q_j` in `Q` and `w` in `Sigma^star` , `delta^star(q_i,w) = q_j` iff there is in `G_M` a walk with label `w` (that is, the edge labels written down as a string are `w`) from `q_i` to `q_j`.
Proof. We give a proof by induction on the length `n geq 0` of `w`. Notice `delta^star(q, epsilon)=q` corresponds exactly with a walk of length `0` in `G_M` . So the `|w|=0` case holds. Assume the statement is true up to some `n`. Let `w=va` where `|v|=n`. (The induction step case.) Suppose `delta^star(q_i,v) = q_k` . By the induction hypothesis there is a walk `W` of length `n` in `G_M` from `q_i`,to `q_k`. If `delta^star(q_i,w) = q_j` we must have `delta^star(q_i,w) = delta (delta^star(q_i,v), a) = q_j` by the definition of `delta^star.` So we have `delta(q_k,a) = q_j`. Thus, if we add to `W` the edge `(q_k, q_j)`, the label on the resulting walk will be `va=w` as desired. This new walk has length `n+1`. It is also not hard to turn this argument around to show if one stated with a walk of length `n+1` with label `w`, that one could show `delta^star(q_i,w) = q_j`. You should do this at home.
If `A_1` and `A_2` are two regular languages, so is their union `A_1 cup A_2`.
Proof. Let `M_1=(Q_1, Sigma, delta_1, q_1, F_1)` and `M_2 =(Q_2, Sigma, delta_2, q_2, F_2)` be the DFAs recognizing languages `A_1` and `A_2`. We would like to make a new DFA, `M`, which simultaneously simulates both `M_1` and `M_2` and accepts a string `w` if either of `M_1` and `M_2` accepts. To simulate both machines at the same time we use a so-called "Cartesian product construction". To do this let `Q = Q_1 times Q_2`. `M`'s alphabet is `Sigma` like that of `M_1` and `M_2`. Define `delta((q, q'), a) = (delta_1(q,a), delta_2(q',a))`. Let the start state of `M` be `(q_1, q_2)`. Finally, let `F = (F_1 times Q_2 )cup (Q_1 times F_2 )`. Verify at home that `M` has the desired properties.
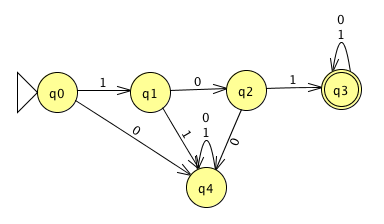
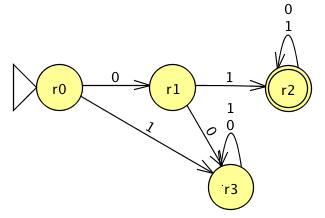
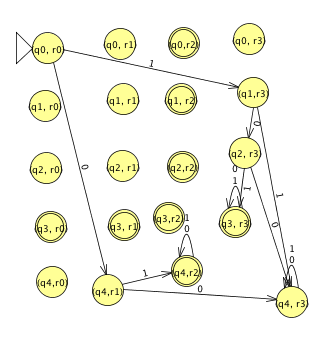
Draw automata for each of the following languages:
Show the automata that results from the product construction.
Post your solutions to the Feb 12 In-Class Exercise Thread.