Outline

• State Minimization
• Building new NFAs out of Old Ones
• Regular Expressions

State Minimization

• We say two states `p`, `q` of a DFA `M` are indistinguishable if `delta^star(p,w) in F` implies `delta^star(q,w) in F` and `delta^star(p,w) !in F` implies `delta^star(q,w) !in F`.
• Otherwise, `p`, `q` are said to be distinguishable.
• Let `p~_I q`,if `p` and `q` are indistinguishable. Notice this is an equivalence relation.
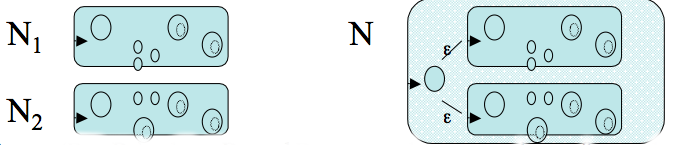
• We now present an algorithm to find the minimal DFA equivalent to `M`.
• The idea is to first compute the equivalence classes of the indistinguishable equivalence relation. Then make one state for each equivalence class, and make an appropriate new transition function.

Procedure for Equivalence

1. Remove all inaccessible states. This can be done by checking for each state if there is a simple path from the start state to it.
2. Consider all pairs `(p,q)` of states. If `p in F` but `q !in F` or vice versa, then mark the pair `(p,q)` distinguishable.
3. Repeat until no previously unmarked pairs are marked:
   1. For all pairs `(p,q)` and all `a in Sigma`, compute `delta(p,a) = p_a` and `delta(q,a) = q_a`. If the pair `(p_a,q_a)` is marked as distinguishable, mark `(p,q)` as distinguishable. Idea: if in `p` `q` on the same letter you transition to distinguishable states then `p` and `q` must be distinguishable.

Procedure to Build Minimal Automaton

1. Use procedure of last slide to generate state equivalence classes for original automata.
2. For each equivalence class `[p] = {q | p~_I q}` create a new state.
3. For each transition rule `delta(r,a)=s` of the original machine, add a transition `delta([r],a)=[s]`.
4. The initial state of the new machine is `[q_0]` where `q_0` was the state of the machine we are trying to minimize.
5. The final states of the new machine is the set `{[f] | f in F}`.

The first procedure for minimizing finite automata was given in Huffman 1954 (J. Franklin Institute. Vol 257. Iss. 3-4).

Our procedure above probably runs in quadratic time, the best known algorithm is `O(n log n)` due to Hopcroft 1971.

There is an important related result known as the Myhill Nerode theorem which is due to Nerode 1958 building on a paper of Myhill 1957. This result can be used to show the automata one gets from our construction is unique up to a renaming of states.

Example

• You can use JFLAP to take an NFA convert it to a DFA and then minimize the result.
• For example, we might start with the following NFA:
  
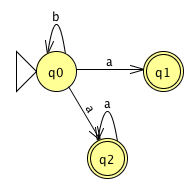
• We can then use JFLAP to get the following DFA (JFLAP will step you through the procedure if you like so you can learn it):
  
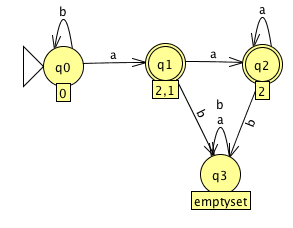
• In the above, I added the trap state with label emptyset and moved around the states to make it prettier looking (I hope).
• Finally, we can convert this last DFA to the minimal DFA:
  
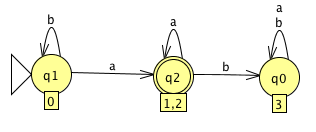
• Since this is a DFA we know we can code it in C or Java. It is also as small as possible so it will be easier to code.

Regular Expressions

• In arithmetic, we can use the operations `+` and `cdot` to build up expressions such as: `(5 + 3) cdot 4`.
• Similarly we can use the regular operations to build up expressions describing regular languages.
• For instance, `0(0 cup 1)^star`.
• This means the language which results from concatenating the language containing 0 with the language of `(0 cup 1)^star`. This in turn is the star of the union of the two languages one containing just `0`; the other containing just `1`.
• These kind of expressions are used in many modern programming languages: Perl, PHP, Python, Java, AWK, GREP.

Formal Definition of a Regular Expression

We say that `R` is a regular expression if `R` over some alphabet `Sigma` is:

1. `a` for some symbol `a` in the alphabet `Sigma`.
2. `epsilon`.
3. `emptyset`.
4. `(R_1 cup R_2)` where `R_1` and `R_2` are regular expressions. `R_1 + R_2` is used by JFLAP, most programming languages use `(R1 | R2)`.
5. `(R_1R_2)` where `R_1` and `R_2` are regular expressions.
6. `(R_1)^star` where `R_1` is a regular expression.

We write `R^+` as a shorthand for `R\ R^star`. Notice also we tend to be lazy on parentheses even thought to be fully well-formed everything has to be completely parenthesized.

We write `L(R)` for the language given by the regular expression.

Regular expressions were first considered in Kleene (1956).

Examples of the Definition

• `0^star10^star={w| w \ mbox{contains a single} \ 1}`
• `(01 cup 10) = {01, 10}`
• `(Sigma Sigma)^star = {w| w \ mbox{is of even length}}`
• `(epsilon cup 0)(epsilon cup 1)= {epsilon ,0,1,01}`
• `1^star emptyset = emptyset`
• `emptyset^star = {emptyset}`

In a programming language like say PHP or Perl you might use things like: "\.|\,|\:|\;|\"|\'|\`|\[|\]|\{|\}|\(|\)|\!|\||\&" to match against, for instance, the punctuation symbols you want.

If you want to see regular expressions gone wild check out the Perl solution to the 99 bottles of beer song.

Equivalence with Finite Automata

• We want to show that a language is regular if and only if some regular expression describes it.
• We will do this in two steps:
  • Prove if a language is described by a regular expression, then it is regular
  • Prove if a language is regular, then it is described by a regular expression.

Proof that regular expression implies regular

• The proof is by induction on the complexity (number of uses of union, `star`, or concatenation) of the regular expression. In the base case, we have regular expressions which make no use of union, `star`, or concatenation.
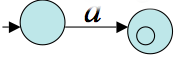
  1. Let `R = a` for some `a` in `Sigma`. Then the following NFA recognizes the languages contain only a:
     
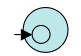
  2. Let `R = epsilon`. Then the following NFA recognizes it:
     
  3. Let `R = emptyset`. Then the following NFA recognizes it:
     

Proof cont'd

Assume now the result holds for languages for which the total number of uses of union, `*`, or concatenation is at most `n`. Consider `R` a regular language of complexity `n+1`. There are three cases to consider:

1. `R` is of the form `(R_1 cup R_2)` where `R_1` and `R_2` are regular expressions of complexity `leq n`. By induction let `N_1` and `N_2` be the machines for `R_1` and `R_2`. Define `N` for `R` as:
   
2. `(R_1R_2)` where `R_1` and `R_2` are regular expressions of complexity `leq n`. By induction let `N_1` and `N_2` be the machines for `R_1` and `R_2`. Define `N` for `R` as:
   
3. `(R_1)^star` where `R_1` is a regular expression of complexity `leq n`. By induction let `N_1` be the machine for `R_1`. Define `N` for `R` as: