










More PDAs, Pumping Lemma for CFGs, Compression
CS154
Chris Pollett
Mar 14, 2011











CS154
Chris Pollett
Mar 14, 2011
Let `P` be a PDA. We want to make a CFG `G` that generates the same language.
The proof that languages given by PDAs and the CFLs are the same is due independently to Chomsky (1962), Schutzenberger (1963), and Evey (1963).
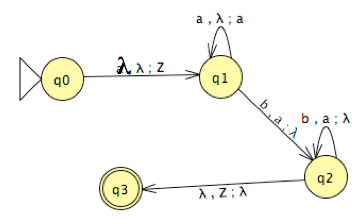
Alternative Proof can convert from PDA to a CFG. Let `N` be a PDA. Without loss of generality we assume the final state of `N` is entered iff the stack is empty. We also assume that any move of `N` increases or decreases the stack content by a single symbol. We set the variables of the simulating CFG to be of the form `(q_iAq_j)` where `q_i` and `q_j` are states of `N`. Our grammar will have rules that ensure that:
`(q_iAq_j) =>^* v`
iff `N` erases `A` from the stack while reading `v` and going from state `q_i` to `q_j`. If our grammar has this property, and we choose `q_(\mbox(start))zq_(\mbox(final))` as the start symbol, then
`q_(\mbox(start))zq_(\mbox(final)) =>^star w`
iff `N` accepts `w`. To complete our proof, we now say the rules of our grammar and leave it to the reader to verify they work. Our grammar consists of two types of rules: (1) rules to handle `N` moves that increase the stack size by `1` -- these have the form: `(q_iAq_j) -> a` for every transition of `N` from some `q_i` to `q_j` which when reading some `a` pops an `A` symbol from the stack; (2) rules to handle transitions from `(q_i,a, A)` to `(q_j, BC)`, these have the form: `(q_iAq_k) -> a(q_jBq_l)(q_lCq_k)` for all possible values of `k` and `l` in the set of states of `N`.
Which of the following is true?
Theorem. If `A` is a context free language, then there is a number `p` (the pumping length) where, if `s` is any string `A` of length at least `p`, then `s` maybe divided into five pieces `s = uvxyz` satisfying the conditions:
Proof. Let `G` be a CFG for our context free language `A`. Let `|V|` be the number of variables in `G`. Let `b` be the maximum number of symbols on the right hand side of a rule. So the maximum number of leaves a parse tree of height `d` can have is `b^d`. We set the pumping length to `p = b^(|V|+1)`. So if `s` is in `A` of length bigger than `p`, its smallest parse tree must be of height greater than `|V|+1`. So some variable `R` must be repeated. So we can do the following kind of surgeries on the parse tree to show Condition 1 of the pumping lemma:
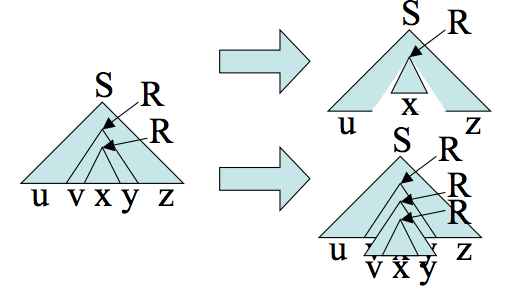 Condition 2 of the pumping lemma will hold since if `v` and `y` were the empty string then the pumped down tree would be a smaller derivations of `s` contradicting our choice of parse tree. Condition 3 can be guaranteed by choosing `R` so both occurrence are among the last `|V|+1` nonterminals of the longest path in the tree. The upper `R` generates `vxy` is therefore of height at most `|V|+1` and so can generate a string of length at most `b^(|V|+1) = p`.
Condition 2 of the pumping lemma will hold since if `v` and `y` were the empty string then the pumped down tree would be a smaller derivations of `s` contradicting our choice of parse tree. Condition 3 can be guaranteed by choosing `R` so both occurrence are among the last `|V|+1` nonterminals of the longest path in the tree. The upper `R` generates `vxy` is therefore of height at most `|V|+1` and so can generate a string of length at most `b^(|V|+1) = p`.
| Letter | `mbox(Aux)` | Production Table | `mbox(Hash)` |
|---|---|---|---|
| a | a | `{}` | `{}` |
| b | ab | `{}` | `{ab}` |
| b | abb | `{}` | `{ab, bb}` |
| a | abba | `{}` | `{ab, bb, ba}` |
| b | abbab becomes AbA | `{A->ab}` | `{Ab, bA}` |
| a | AbAa | `{A->ab}` | `{Ab, bA, Aa}` |
| b | AbAab becomes AbAA | `{A->ab` marked} | `{Ab, bA, \A\A}` |
| b | AbAAb becomes BAB | `{A->ab` marked, `B->Ab}` | `{\B\A, \A\B}` |
| a | BABa | `{A->ab` marked,`B->Ab}` | `{\B\A, \A\B, \B\a}` |
| b | BABab becomes BABA becomes CC | `{A->ab` marked, `B->Ab`, `C->BA}` | `{\C\C}` |
| b | CCb | `{A->ab` marked, `B->Ab`, `C->BA}` | `{\C\C, \C\b}` |
| a | CCba | `{A->ab` marked, `B->Ab`, `C->BA}` | `{\C\C, \C\b, ba}` |
| b | CCbab becomes CCbA | `{A->ab` marked, `B->Ab`, `C->BA}` | `{\C\C, \C\b, \b\A}` |
| b | CCbAb becomes CCB | `{A->ab` marked, `B->Ab` marked, `C->BA}` | `{\C\C, \C\B}` |