Formal Definition

At the end of Monday, we gave the following formal definition of deterministic finite automata (DFA):

A deterministic finite automaton is a 5-tuple `(Q, Sigma, delta, q_0, F)`, where
1. `Q` is a finite set called the states.
2. `Sigma` is a finite set called the alphabet.
3. `delta:Q times Sigma rightarrow Q` is the transition function.
4. `q_0 \in Q` is the start state.
5. `F subseteq Q` is the set of accept states.
The transition function tells us if we are in a given state reading a given symbol what is the next state to go to.

Example of the Definition

Consider the machine:
The corresponding five tuple for this machine has:
1. `Q = {q_1, q_2, q_3}`,
2. `Sigma = {0, 1}`,
3. `delta` is the function given by:
  `(q_1, 0) mapsto q_1`, `(q_2, 0) mapsto q_3`, `(q_3, 0) mapsto q_2`,
  `(q_1, 1) mapsto q_2`, `(q_2, 1) mapsto q_2`, `(q_3, 1) mapsto q_2`
4. `q_1` as the start state,
5. `F = {q_2}`.

Implementing Finite Automata -- Base Class

Suppose we had the job of implementing a finite automata in Java.
Typically, we would want to process strings according to how the finite automata would process them.
To make our set-up as flexible as possible we should probably have a base class that implements the core string processing algorithm.
Then in sub-classes specify the transition function, start state, and final states to use.

An example base class might be:

public abstract class Automata
{
    public Automata()
    {
    }

    public void setState(int state)
    {
        currentState = state;
    }

    public boolean processString(String w) 
    {
       for(int i = 0; i < w.length(); i++)
       {
           currentState = delta(currentState, w.charAt(i));
       }
       boolean accept = finalState(currentState);
       return accept;
    }

    public abstract int delta(int state, char c);
    public abstract boolean finalState(int state);

    int currentState;
}

Implementing Finite Automata -- Specific Automata

Now if we wanted to implement the automata of a couple slides ago we could write:

public class TestAutomata extends Automata
{
    public TestAutomata()
    {
    }

    public int delta(int state, char c)
    {
        int outState = 1;
        switch(state)
        {
            case 1:
                if(c == '0') 
                {
                    outState = 1;
                } 
                else 
                {
                    outState = 2;
                }
            break;

            case 2:
                if(c == '0')
                {
                    outState = 3;
                }
                else 
                {
                    outState = 2;
                }
            break;

            case 3:
                outState = 2;
            break;
        }
        return outState;
    }

    public boolean finalState(int state)
    {
        return (state == 2) ? true : false;
    }

    public static void main(String args[])
    {
        TestAutomata test = new TestAutomata();
        test.setState(1);
        if(args.length == 0 ){
            System.out.println("It is not recognized by this automata.");
        }
        System.out.println("Checking the string "+ args[0]);
        if(test.processString(args[0])) 
        {
            System.out.println("It is recognized by this automata.");
        }
        else
        {
            System.out.println("It is not recognized by this automata.");
        }
    }
}

Comments on Code

Notice the only memory requirements besides the input string are all constant. For example, 4 bytes to store the int for the currentState -- so DFAs are very memory efficient.
Notice also to determine if the string was in the language we made a single scan on the input string and at each step while scanning only process a fixed number of instructions.
So the processing was linear time in the input length. i.e., very fast.

Formal Definition of Accepting a String

Let `M= (Q, Sigma, delta, q_0, F)` be a finite automaton and let `w=w_1 w_2 ldots w_n` be a string. Then `M` accepts `w` if a sequence of states `r_0 r_1 ... r_n` in `Q` exist satisfying:
1. `r_0=q_0`
2. `delta(r_i, w_(i+1)) = r_(i+1)`, for `i=0,1, ldots , n-1`,
3. `r_n in F`.
That the string `0100` is accepted by the automata of a few slides ago is witnessed by the sequence of states `q_1 q_1 q_2 q_3 q_2`. Notice this is a walk on the automata viewed as a labeled graph.
We write `L(M)` for the language that `M` accepts. That is, those strings that `M` accepts.
Given a set of strings `S`, we say `M` recognizes `S` if `L(M)=S`.
So `M_1` of a couple slides back recognizes `{ w | w \ mbox{contains at least one 1 and an even number of 0s follow the last 1}}`
A language is called a regular language if some finite automaton recognizes it.

The Extended Transition Function

Let `M= (Q, Sigma, delta, q_0, F)` be a finite automaton and let `w=w_1w_2 ldots w_n` be a string.
We define the extended transition function `delta^star:Q times Sigma^star rightarrow Q` inductively:
1. `delta^star(q, epsilon) rightarrow q`
2. `delta^star(q, wa) rightarrow delta(delta^star(q,w),a)`
Intuitively, the equation `delta^star(q, w) =q'` tells us that if we are in state `q` when we begin to process the string `w`, then after processing `w` we will be in state `q'`.
An equivalent to the last slide's way to define `M` accepts `w` is to say, `M` accepts `w` if for some `q in F` we have `delta^star(q_0, w)=q`. i.e., we start in the start state `q_0`, process `w`, and end up in an accept state.

Designing Automata

Suppose we want to recognize the language that consists of an odd number of 1s.
One approach is to "pretend to be the automaton".
You get symbols from {0,1} one by one.
Ask how much of the string so far do we read to remember in order to decide whether to accept or not? In this particular case, we just need to remember if we are currently even or currently odd.
Now we make make each of these possibilities states. Next we pretend we are in one of the states and see a symbol. What do we do?
Finally, we figure out what our accept and final states are:

Trap States

For DFA, we require `delta` to be a total function.
This means for every state `q` and every alphabet symbol `a`, `delta(q,a)` must return some state `q'`.
That `delta` is total will force `delta^star` to be total as well.
Consider the problem of designing an automaton for the language: `{w | w = a^nb \ mbox{for some}\ n geq 0}`.
On a string like `aabab`, after the third `a` we know the string is not in the language; nevertheless, since the transition function is total we still need to continue processing the string until it is done.
This can be done with a trap state, which has a loop back to itself for every alphabet symbol.

Walks on Automata

Theorem

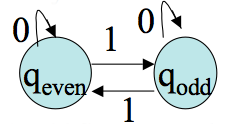
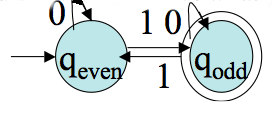
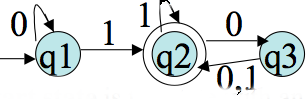
Let `M= (Q, Sigma, delta, q0, F)` be a DFA, and GM be its associated transition graph. Then for every `q_i`, `q_j` in `Q` and `w` in `Sigma^star` , `delta^star(q_i,w) = q_j` iff there is in GM a walk with label `w` (that is, the edge labels written down as a string are `w`) from `q_i` to `q_j`.

Proof. We give a proof by induction on the length `n geq 0` of `w`. Notice `delta^star(q, epsilon)=q` corresponds exactly with a walk of length `0` in GM . So the `|w|=0` case holds. Assume the statement is true up to some `n`. Let `w=va` where `|v|=n`. (The induction step case.) Suppose `delta^star(q_i,v) = q_k` . By the induction hypothesis there is a walk `W` of length `n` in GM from `q_i`,to `q_k`. If `delta^star(q_i,w) = q_j` we must have `delta^star(q_i,w) = delta (delta^star(q_i,v), a) = q_j` by the definition of `delta^star.` So we have `delta(q_k,a) = q_j`. Thus, if we add to `W` the edge `(q_k, q_j)`, the label on the resulting walk will be `va=w` as desired. This new walk has length `n+1`. It is also not hard to turn this argument around to show if one stated with a walk of length `n+1` with label `w`, that one could show `delta^star(q_i,w) = q_j`. You should do this at home.

Regular Operations

Just as the natural number are closed under operations like addition and multiplication, the regular languages enjoy some closure properties:
- Union `A cup B = {x| x in A or x in B}`.
- Concatenation `AB = {xy | x in A ^^ y in B}`
- Star `A^star = {x_1 x_2 ldots x_k| k geq 0 \ mbox{and each} \ x_i in A }`
This closure conditions require proof. We will prove the first one today. We will show the last two after we introduce nondeterministic finite automata.

More Deterministic Finite Automata

Outline