Outline

• Three methods of solving recurrences
• Quiz
• Heaps

Introduction

• Last week, we tried to argue that analyzing divide-and-conquer algorithms frequently involves solving recurrences.
• Therefore, it is important to be able to solve recurrences.
• As evidence for this, we gave divide-and-conquer algorithms for merge sort, maximum subarray, matrix multiply, and Strassen's matrix multiply.
• For each, the run time analysis in turn involved solving a recurrence.
• We said there were three common techniques for solving recurrences: the substitution method, the recursion tree method, and the master method.
• We started talking about the substitution method and that is where we resume our story today.

The Substitution Method

• Last day, we used the substitution method to solve `T(n) = 2T(lfloor n/2 rfloor) +n`
• Recall we often omit the base case when we state such recurrence and assume for small `n` that `T(n)` is `Theta(1)`.
• The idea to solve this recurrence was we guess the answer `T(n) = O(n log n)`, then used induction to prove `T(n) le c nlog n` for an appropriate choice of `c >0`.
• So how do you make a good guess?
• Well, if the recurrence is similar to one you have seen before then you might guess a similar answer.

More on Substitution Guess Choice

• For example, consider the recurrence `T(n) = 2T(lfloor n/2 rfloor +17 ) +n`.
• This is almost identical to the recurrence of the last slide.
• Further adding a constant to `lfloor n/2 rfloor` we yield a number close to `lfloor n/2 rfloor` when `n` is large.
• So we might guess `T(n) = O(n log n)`.
• It turns out this correct.
• Another way to come up with a guess is to look for an initial lower and upper bound then try to zero in on a guess.
• For example, in the above recurrence, we add `+n` even at the `T(n)` stage, so we know the answer is `Omega(n)`.
• It is also not to hard to give an initial upper bound of `O(n^2)`. From these two initial bounds we can then try to hone in towards the correct answer.

Subtleties

• Consider `T(n) = T(lfloor n/2 rfloor) + T(|~n/2~|) +1`.
• As a guess we might try `T(n) = O(n)` and try to show `T(n) le cn` for some `c>0`.
• Substituting our guess gives:
  `T(n) le c lfloor n/2 rfloor + c|~ n/2 ~| +1 = c n+1`
• Unfortunately, this does not imply `T(n) le cn` for any choice of `c`.
• However, the correct is `O(n)`. So how do we make the argument go through?
• Instead, of trying to show `T(n) le cn` we instead try to show `T(n) le cn -d` for some `d ge 1`. Notice this will imply `T(n) le cn`.
• But now, substituting gives:
  `T(n) le c(lfloor n/2 rfloor -d) + c(|~ n/2 ~| - d) + 1`
  `= cn - 2d + 1`
  `le cn - d`.
  So the argument goes through.

Changing Variables

• Sometime we can make an unfamiliar recurrence into a familiar one by doing a change of variables.
• For example, consider the recurrence
  `T(n) = 2T(lfloor sqrt(n) rfloor) + log n`.
• Letting `m = log n` and rewriting the recurrence in terms of `m` gives
  `T(2^m) = 2T(2^(m/2)) + m`.
• Letting `S(m) = T(2^m)` we get the recurrence
  `S(m) = 2S(m/2) +m`
  which we solved before
• So we know `S(m) = O(m log m)`
• Changing back from `S(m)` to `T(n)` gives
  `T(n) = T(2^m) = S(m) = O(mlog m) = O(log n log log n)`.

Quiz (Sec 5)

Quiz (Sec 6)

The Recursion Tree Method

• We have already seen this method a couple of times.
• When we tried to analyze merge sort, we expanded out the recursion tree and worked out the amount of work performed at each level.
• Adding these together gave us the run-time bounds.
• We used a similar analysis for matrix multiplication, and Strassen's algorithm.
• A recursion tree is a tree where each node represents the cost of a single subproblem somewhere in the set of recursive function invocations.
• We sum the costs within each level of the tree to obtain a set of per-level costs, and then we sum all the per-level costs to determine the total cost.

Recursion Tree Example

• Consider the recurrence `T(n) = 3T(lfloor n/4 rfloor) +Theta(n^2)`.
• We want to use the recursion tree to get us a good guess which we can verify using the substitution method.
• Above is the recursion tree for `T(n) = 3T(n/4) + cn^2` for some `c > 0`.
• To keep things simple, we assume `n = 4^k` for some `k`. (a) where we have done no expansion, (b) represents expanding 1 level, (c) represents expanding two levels, and the bottom figure represents expanding the whole tree.
• At depth `i`, the subproblem size is `n/4^i`. So when `i= log_4 n` the problem size will be `1` and the expansions will stop.
• Thus, the tree has `log_4 n +1` levels. There are `3^i` nodes at level `i` and for each node at level `i` we do `c(n/4^i)^2` work before splitting into subproblems. So the total cost of level `i` is `(3/16)^ic n^2`.
• The bottom node each has cost `T(1)` and there `3^(log_4 n)= n^(log_4 3)` many nodes. So the cost of the last row is `Theta(n^(log_4 3))`.

More on the example

• Summing up all the levels gives the equations
  `T(n) = sum_(i=0)^(log_4 n - 1)(3/16)^icn^2 + Theta(n^(log_4 3))`
  using our formula for geometric series
  `= ((3/16)^(log_4 n) - 1)/((3/16) - 1)c n^2 + Theta(n^(log_4 3))`.
• This last formula seems messy if our goal is to come up with a good bound for the recurrence, so we back up a step and notice
  `T(n) = sum_(i=0)^(log_4 n - 1)(3/16)^icn^2 + Theta(n^(log_4 3))`
  `< sum_(i=0)^(infty)(3/16)^icn^2 + Theta(n^(log_4 3))`
  `= 1/(1 - (3/16))cn^2 + Theta(n^(log_4 3))`
  `= 16/13 c n^2 + Theta(n^(log_4 3))`
  `= O(n^2)`
• So we guess `T(n) = O(n^2)` for our recurrence.
• So we want to show `T(n) le dn^2` for some constant `d >0`.
• We have
  `T(n) le 3T(lfloor n/4 rfloor) +cn^2`
  `le 3d (lfloor n/4 rfloor)^2 + cn^2`
  `le 3d(n/4)^2 + c n^2`
  `= 3/16 dn^2 + cn^2`
  `le d n^2` provided `d > (16/13)c`.

The Master Method

• The master method allows one to solve recurrences of the form
  `T(n) = a T(n/b) + f(n)` where `a ge 1` and `b > 1` and `f(n)` is an asymptotically positive function.
• To use this method you need to memorize the three cases of the following theorem.

Master Theorem

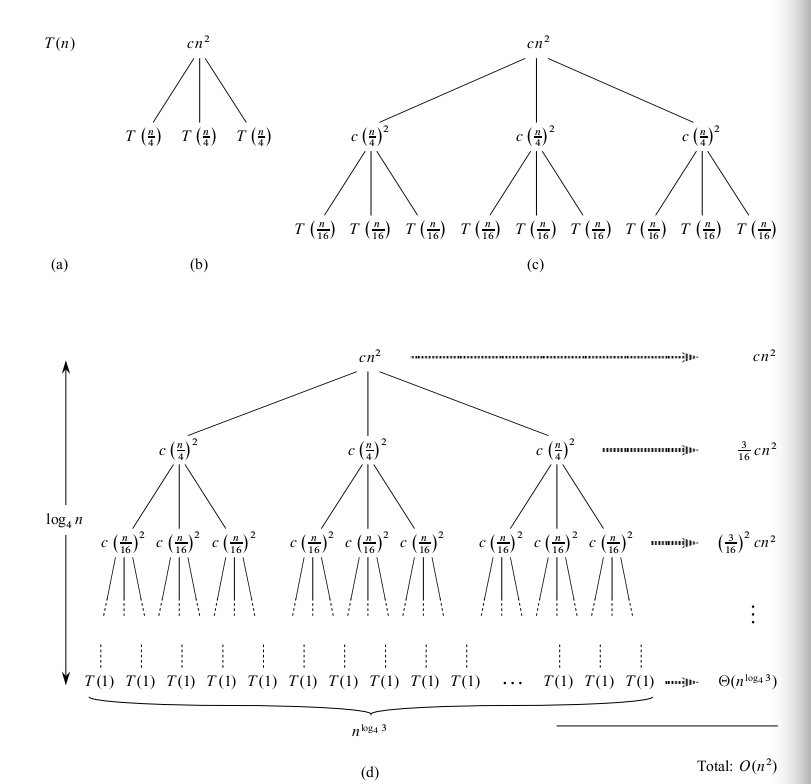
Let `a ge 1` and `b > 1` be constants, let `f(n)` be a function, and let `T(n)` be defined on the nonnegative integers by the recurrence
`T(n) = aT(n/b) + f(n)`, where we interpret `n/b` to mean either `lfloor n/b rfloor` or `|~n/b~|`. Then `T(n)` has the following asymptotic bounds:

1. If `f(n) = O(n^(log_b a - epsilon))` for some `epsilon > 0`, then `T(n) = Theta(n^(log_b a))`.
2. If `f(n) = Theta(n^(log_b a))`, then `T(n) = Theta(n^(log_b a)log n)`.
3. If `f(n) = Omega(n^(log_b a + epsilon))` for some `epsilon > 0`, and if `af(n/b) le c f(n)` for some constant `c <1` and all sufficiently large `n`, then `T(n) = Theta(f(n))`.

• We will not prove the Master Theorem in this class, but will give some intuitions on it on the next slide.

Remarks on the Master Theorem

• In each of the three cases, we compare `f(n)` with the function `n^(log_b a)`.
• Intuitively, the larger of the two functions determines the solution to the recurrence.
• Case (1) is when `n^(log_b a)` is larger. In this case the solution is `Theta(n^(log_b a))`.
• Case (2) they are asymptotically the same size, in which case we get a log factor tacked on `Theta(n^(log_b a)log n)`
• Case (3), `f(n)` is larger in which case the recurrence grows as `T(n) = Theta(f(n))`.
• The `epsilon` in the exponent of case (1) and (3) requires that the difference between `n^(log_b a)` and `f(n)` must be at least a polynomial factor

Examples Using the Master Method

• Consider `T(n) = 9 T(n/3) + n`. So `a=9`, `b=3`, and `f(n) = n`. `n^(log_b a) = n^(log_3 9)= Theta(n^2)`. Since `f(n) in O(n^(log_3 9 -epsilon))`, where `epsilon = 1`, we can apply case 1 of the Master theorem and conclude `T(n) = Theta(n^2)`.
• As a second example, consider `T(n) = T((2n)/3) + 1`, `a = 1`, `b = 3/2`, `f(n) = 1`, and `n^(log_b a) = n^(log_(3/2) 1) = n^0 = 1`. Case 2 applies since `f(n) = Theta(n^(log_b a)) = Theta(1)`, and thus the solution to the recurrence is `T(n) = Theta( log n)`.
• Suppose `T(n) = 3T(n/4) + n log n`. Then we have `a=3`, `b=4`, `f(n) = n log n`, and `n^(log_b a) = n^(log_4 3) = O(n^(0.793))`. Since `f(n) = Omega(n^(log_4 3 + epsilon))` where `epsilon approx 0.2`, case 3 applies if we can show the regularity condition holds for `f(n)`. For sufficiently large `n`, we have that `a f(n/b) = 3(n/4) log(n/4) le (3/4) nlog n = cf(n)` for `c= 3/4`. So by case, 3, `T(n) = Theta(n log n)`.

Heaps

• We are now going to look at a data structure, called a heap which will help us come up with another `Theta(n log n)` sorting algorithm.
• Heaps have many other uses besides sorting and we will also look at these over the next day or so.
• A (binary) heap is a nearly complete binary tree. All rows must be filled except for perhaps the last.
• An array `A` that represents a heap is an object with two attributes `A.text(length)`, which gives the number of lements in the array, and `A.\text(heap-size)`, which represents how many elments in the heap are stored within array `A`.
• The root of the tree is `A[1]`, and given the index `i` of a node the indices of its parent, left child, and right child are computed as follows:
  Parent(i) := `lfloor i/2 rfloor`
  Left(i) := `2i`
  Right(i) := `2i+1`

Max/Min Heaps

• There are two kinds of binary heaps: max-heaps and min-heaps.
• A max-heap is a heap that satisfies the max heap property, that is, that for every node `i`, A[Parent(i)] `ge` A[i].
• A min-heap is a heap that satisfies the min heap property, that is, that for every node `i`, A[Parent(i)] `le` A[i].
• In this class, we will present our algorithms using max-heaps, but they could just as easiliy have been presented using min-heaps.
• We will present some algorithms on Wednesday.