Outline

• Rotations of Red Black Trees
• Insert

Introduction

• Last week, we discussed binary search trees (BSTs) and gave `O(h)` time algorithms, where `h` is the height of the tree, for each of the dynamic set operations when done a BST.
• In the worst case, this height though might be linear in the number of items in the tree.
• On Monday, we said the expected height of a BST that results from inserting a randomly permuted set of input values is `O(log n)` where `n` is the number of values.
• Ideally, we want to modify our BSTs so that we can be sure that they are always logarithmic height. This leads to the idea of self-balancing trees, trees whose insert/delete operations preserve that the height of the tree will tend to be logarithmic.
• There are many kinds of self-balancing trees: AVL trees, splay trees, 2-3 trees, 2-3-4 trees, B-trees.
• The book presents red-black trees. These are BSTs where each node is labelled as being either red or black, the root and nil pointer leaves are all black, all paths in a tree starting at the same node will traverse the same number of black nodes before hitting a leaf, and where the child of a red node is always black.
• We proved last day that red-black trees have height `2log(n + 1)`.
• We said that the ingredient needed to modify insert and delete so that they preserve the red-black property was the concept of rotation.
• The reason why red black trees are superior in a RAM setting to the other self-balancing tree types mentioned above is that: (1) insert and delete on a RB-tree requires only constantly many rotations (as opposed to non-constantly many for AVL and splay-tree), (2) the node structure is of fixed size (the same as that of a BST except for a field for color) for all elements in the tree (2-3, 2-3-4, and B-trees)) So RB-trees will tend to be faster.
• Let's continue the story...

Pseudo-code for Left-Rotate

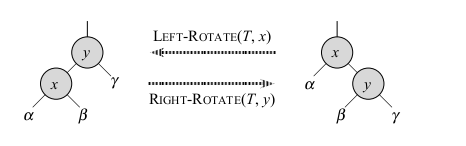
• The picture above illustrates the tree surgery needed to do a left/right rotation of a tree. Notice if the tree was a BST before the operation, it will be a BST afterwards.
• Below is the pseudo-code for LEFT-ROTATE. The pseudo-code for RIGHT-ROTATE is completely analogous except the words left and right would be reversed everywhere:

  LEFT-ROTATE(T,x)
  01 y = x.right  //set y
  02 x.right = y.left  //turn y's left subtree into x's right subtree
  03 if y.left != T.nil
  04    y.left.p = x
  05 y.p = x.p  // link x's parent to y
  06 if x.p == T.nil
  07    T.root = y
  08 elseif x == x.p.left
  09    x.p.left = y
  10 else x.p.right = y
  11 y.left = x  //put x on y's left
  12 x.p = y
  

Insertion

• We next give a procedure for inserting into an `n`-node red-black tree in `O(log n)` time.
• To do this we modify our TREE-INSERT procedure for BSTs. We do TREE-INSERT(T,z) first, color the node `z` red, and then call as fix-up procedure to recolor nodes and perform rotations to make the tree back into a red-black one.
• We assume the key value has already been filled into the node `z` we are about to insert into the tree. Here is the procedure:

  RB-INSERT(T, z)
  01 y = T.nil
  02 x = T.root
  03 while x != T.nil //find where to insert
  04    y = x
  05    if z.key < x.key
  06        x = x.left
  07    else x = x.right
  08 z.p = y  //insert node
  09 if y == T.nil //tree empty
  10    T.root = z
  11 elseif z.key < y.key
  12    y.left = z
  13 else y.right = z
  14 z.left = T.nil
  15 z.right = T.nil
  16 z.color = RED // add color then fix red black property
  17 RB-INSERT-FIXUP(T,z)
  

RB-INSERT-FIXUP

• Let's consider how we might need to fix-up the tree to make it a red-black tree again.
• First, let's look at the fix-up code:

  RB-INSERT-FIXUP(T,z)
  01  while z.p.color == RED
  02     if z.p == z.p.p.left
  03         y = z.p.p.right
  04         if y.color == RED
  05             z.p.color = BLACK  //case 1
  06             y.color = BLACK    //case 1
  07             z.p.p.color = RED  //case 1
  08             z = z.p.p          //case 1
  09         else if z == z.p.right
  10                  z = z.p            //case 2
  11                  LEFT-ROTATE(T, z)  //case 2
  12             z.p.color = BLACK      //case 3
  13             z.p.p.color = RED      //case 3
  14             RIGHT-ROTATE(T, z.p.p) //case 3
  15      else (same as then clause with "right" and "left" exchanged
  16  T.root.color = BLACK
  

Fix-up Remarks

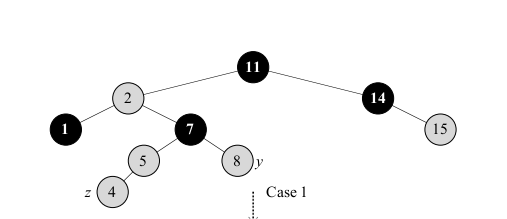
• After the initial TREE-INSERT, every node will still be red or black (so Property 1 or RB-tree will hold).
• The leaves (T.NIL) will still be black so Property 3 holds.
• Property 5 says that the number of black nodes along any path starting at a given node is the same. Since we added a red node. This property will also hold.
• Property 2 requires the root to be black. Before our fix-up, this might fail if the `z` inserted ends up as the root.
• Property 4 might fail if both children of `z` are not black. The insert of `z` in the image above shows this case.

Fix-Up Loop Invariant

• The while loop, lines 1-15 of the fix-up code maintain the following three-part loop invariant: At the start of each iteration of the loop:
  1. Node z is red.
  2. If z.p is the root, then z.p is black
  3. If the tree violates any of the red-black properties, then it violates at most one of them, and the violation is of either property 2 or property 4. If the tree violates property 2, it is because `z` is the root and z is red. If the tree violates property 4, it is because both `z` and `z.p` are red.
• Part (3) will be useful in showing our fix-up code restores the red-black property
• Part (1) is useful so we know the color of the node we are working with.
• Part (2) will be useful in showing that z.p.p exists when we need to reference it in the fix-up code.

Proof of Loop Invariant

To show the loop invariance of the property of the last slide, we need to prove Initialization, Maintenance, and Termination conditions. We will prove these slightly out of order on the next few slides, starting below

Initialization: Prior to the first iteration of the loop, we started with a red-black tree with no violations and we added the red node `z`. We show each part of the invariant holds at the time RB-INSERT-FIXUP is called:

1. When RB-INSERT-FIXUP is called, `z` is the red node that was added.
2. If z.p is the root, then z.p started out black and did not change prior to the call of RB-INSERT-FIXUP.
3. We have already seen that properties 1, 3, and 5 hold when RB-INSERT-FIXUP is called. If the tree violates property 2, then the red root must be the newly added node `z`, which is the only internal node in the tree. Because the parent and both children of `z` are the sentinel, which is black, the tree does not violate property 4. Thus, this violation of property 2 is the only violation of red-black properties in the entire tree. If the tree violates property 4, then, because the children of node `z` are black sentinels and the tree had no other violations prior to `z` being added, the violation must be because both `z` and `z.p` are red. Moreover, the tree violate no other red black properties.

Termination

When the loop terminates, it does so because `z.p` is black. (If `z` is the root, then `z.p` is the sentinel T.nil, which is black). Thus, the tree does not violate property `4` at loop termination. By the loop invariant, the only property that might fail to hold is property 2. Line 16 restores this property, too, so that when RB-INSERT-FIXUP terminates, all the red-black properties hold.

Maintenance

There are six cases in the while loop, but three are symmetric to the other three, depending on whether line 2 determines `z`'s parent `z.p` to be a left child or a right child of `z`'s grandparent `z.p.p`. We have given the code only for the situation in which `z.p` is a left child. We know `z.p.p` exists since by part (2) of the loop invariant, if `z.p` is the root, then `z.p` is black. Since we enter a loop iteration only if `z.p` is red, we know that z.p cannot be the root, so `z.p.p` exists.

We distinguish case 1 from cases 2 and 3 by the color of `z`'s parent's sibling or "uncle". Line 3 makes `y` point to `z`'s uncle `z.p.p`.right, and line 4 tests `y`'s color. If `y` is red, then we execute case 1. Otherwise, control passes to cases 2 and 3. In all three cases, `z`'s grandparent `z.p.p` is black, since its parent `z.p` is red, and property 4 is violated only between `z` and `z.p`.

More Maintenance -- Case 1 z's uncle y is red

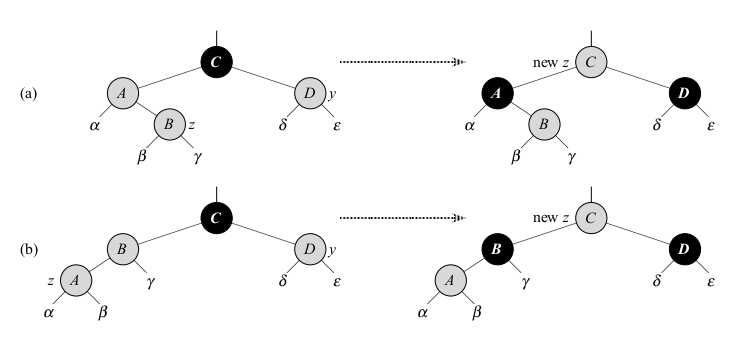
The above picture illustrates this case. here both `z.p` and `y` are red. Because `z.p.p` is black, we can color both `z.p` and `y` black, thereby fixing the problem of `z` and `z.p` both being red, and we can color `z.p.p` red, thereby maintaining property 5. We then repeat the while loop with `z.p.p` as the new node `z`. Let's verify the loop invariant properties. Let `z' = z.p.p` denote the new `z`.

1. Because this iteration colors `z.p.p` red, node `z'` is red at the start of the next iteration.
2. The node `z'.p` is `z.p.p.p` in this iteration, and the color of this node does not change. If this node is the root, it was black prior to this iteration, and it remains black at the start of the next iteration.
3. We have already argued that case 1 maintains property 5, and it does not introduce a violation of 1 and 3.
   If node `z'` is the root at the start of the next iteration, then case 1 corrected the lone violation of property 4. Since `z'` is red and it is the root, property 2 fails and it is only property violated, and this violation is due to `z'`.
   If node `z'` is not the root at the start of the next iteration, then case 1 has not created a violation of property 2. Case 1 corrected the lone violation of property 4 that existed at the start of this iteration. It then made `z'` red and left `z'.p` alone. If `z'.p` was black, there is no violation of property 4. If `z'.p` was red, coloring `z'` red created one violation of property 4 between `z'` and `z'.p`.

More Maintenance -- Case 2 and Case 3

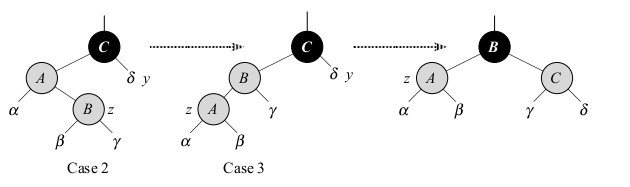
Case 2 is when `z`'s uncle `y` is black and `z` is a right child. Case 3 is the same but `z` is a left child.

Case 2 and 3 are shown in the above figure.

Line 10-11 handle case 2. In case 2, node `z` is a right child of its parent. We use a left rotation to transform the situation into case 3, in which node `z` is a left child. Because `z` and `z.p` are red, the rotation affects neither the black height nor property 5. `z`'s uncle is now black as it would be in case 3.

To fix case 3, we do a right rotation as in the figure above and label the root black and C in the above red. Since `z`'s uncle was black and `z.p`'s right child was black. `C` will satisfy the red-black property. We have also fixed the only violation in the tree of property 4. Node B is now the root of the affected subtree and is black, so even if B were the root of the whole red-black tree, property two that the root is black will hold. Node `z` is still red above so (1) of our loop invariant holds, we have also just argued (2) and (3) hold. In fact, after this change the whole tree will be red back and the while loop will terminate.

Notice in total the fix code does at most 2 rotations. As is moves up the tree it will be `O(log n)`. So the whole procedure is `O(log n)`.