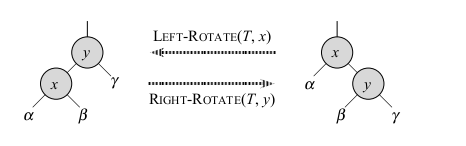
Red-Black Trees
CS146
Chris Pollett
Apr 14, 2014











CS146
Chris Pollett
Apr 14, 2014
Which of the following statements is true?
Which of the following statements is true?
The folowing lemma shows that red-black trees make good search trees:
Lemma. A red-black tree with `n` internal nodes has height at most `2log(n+1)`.
Proof. We claim first that the subtree rooted at any node `x` contains at least `2^(bh(x)) - 1` internal nodes. We prove this claim by induction on the height of `x`. If `x` has height `0`, then `x` must be a leaf, and the subtree rooted at `x` contains `2^(bh(x)) - 1 = 2^0 - 1 = 0` internal nodes. For the induction step,
let `x` be a node of positive height and suppose it is an internal node with two children. A child will have black-height `bh(x)` if the child is red and `bh(x) - 1` if the child is black. Since the child of `x` has less height than `x`, we can apply the induction hypothesis to conclude that each child has at least `2^(bh(x) - 1) -1` internal nodes. So the subtree root at `x` had at least
`(2^(bh(x) -1) - 1) + (2^(bh(x) -1 ) - 1) + 1 = (2^(bh(x)) - 1)` internal nodes. So the induction hypothesis holds in this case.
To complete the proof of the lemma, let `h` be the height of the tree. By Property 4, at least half the nodes on any simple path from the root to a leaf, not including the root must be black. So the black height must be at least `h/2`. So `n ge 2^(h/2) -1`. Moving `1` to the right hand side and taking logarithms on both sides yields
`log(n+1) ge h/2` or `h le 2log(n + 1)`.