










Linear Time Search
CS146
Chris Pollett
Mar 10, 2014











CS146
Chris Pollett
Mar 10, 2014
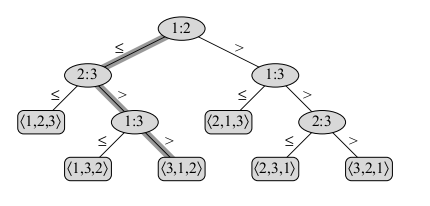
Which of the following statements is true?
Which of the following statements is true?
COUNTING-SORT(A, B, k) 1 let C[0..k] be a new array 2 for i = 0 to k 3 C[i] = 0 4 for j = 1 to A.length 5 C[A[j]] = C[A[j]] + 1 6 // C[i] now contains the number of elements equal to i 7 for i = 1 to k 8 C[i] = C[i] + C[i - 1] 9 // C[i] now contains the number of elements less than or equal to i 10 for j = A.length downto 1 11 B[C[A[j]]] = A[j] 12 C[A[j]] = C[A[j]] - 1

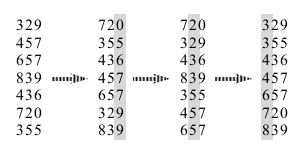
RADIX_SORT(A,d) 1 for i = 1 to d 2 use a stable sort to sort array A on digit i
Lemma. Given `n` d-digit numbers in which each digit can take on up to `k` possible values, RADIX-SORT correctly sorts these numbers in `Theta(d(n+k))` time if the stable sort it uses takes `Theta(n + k)` time.
Proof. The correctness of radix sort follows by induction on the columns being sorted. The induction hypothesis is that after the `m`th stable sort the numbers are in sorted order according to their least `m` significant digits. The analysis of the running time depends on the stable sort used as the intermediate sorting algorithm. When each digit is in the range `0` to `k-1`, and `k` is not too large, counting sort is the obvious choice. Each pass over `n` `d`-digit numbers then takes time `Theta(n+k)`. There are `d` passes, and so the total time for radix sort is `Theta(d(n + k))`. QED
Lemma. Given `n` `b`-bit numbers and any positive `r le b`, RADIX-SORT correctly sorts these numbers in `Theta((b/r)(n+2^r))` time if the stable sort it uses takes `Theta(n +k)` time for inputs in the range `0` to `k`.
Here we can view `r` as being the number of bits needed to represent a digit in some other base than binary.
Proof. For a value `r le b`, we view each key as having `d = |~b/r~|` digits of `r` bits each. Each digit is an integer in the range `0` to `2^(r) - 1`, so we can use counting sort with `k = 2^r -1`. Each pass of counting sort takes time `Theta(n + k) = Theta(n + 2^r)` and there are `d` passes, for a total running time of `Theta(d(n+2^r))= Theta((b/r)(n+2^r))`. QED