Mergesort, Recurrences
CS146
Chris Pollett
Feb 10, 2014











CS146
Chris Pollett
Feb 10, 2014
The basic idea is that we image having two piles of items. We look at the top item in each pile and move the smaller to an output pile, continuing until all the items have been placed in the output pile.
MERGE(A, p, q, r)
1 n1 = q - p + 1
2 n2 = r - q
3 let L[1..n1+1] and R[1..n2+1] be new arrays
4 for i = 1 to n1
5 L[i] = A[p + i - 1] //copy to first subarray to L
6 for j = 1 to n2
7 R[j] = A[q +j] //copy second subarray to R
8 L[n1 + 1] = infinity // a value bigger than any value in the array
9 R[n2 + 1] = infinity // acts as a "sentinel" value so will never
// go off end of array
10 i = 1
11 j = 1
12 for k = p to r
13 if L[i] <= R[j]
14 A[k] = L[i]
15 i = i + 1
16 else
A[k] = R[j]
17 j= j + 1
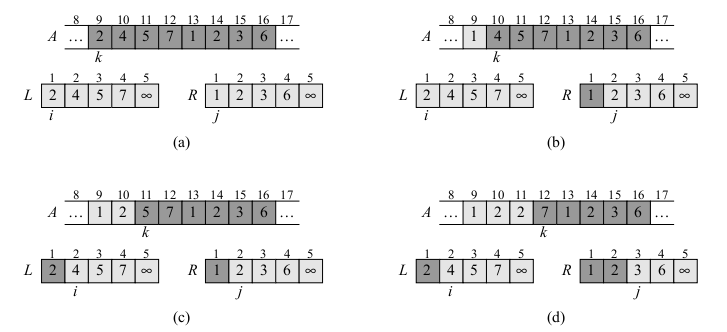
Which of the following statements is true?
Which of the following statements is true?
At the start of each iteration of the for loop of lines 1-8, `A[1, .. j-1]` consists of the elements originally in `A[1 .. j-1]`, but in sorted order.
Claim. MERGE satisfies the following loop invariant:
At the start of each iteration of the for loop of lines 12-17, the subarray `A[p..k-1]` contains the k - p smallest elements of `L[1..n1 + 1]` and `R[1..n2 + 1]` in sorted order. Moreover, `L[i]` and `R[j]` are the smallest elements of their arrays that have not been copied back to `A`.
Proof. We need to show the three properties of loop invariants:
Given our MERGE subroutine we are now in a position to present the MERGE-SORT algorithm:
MERGE-SORT(A,p,r) 1 if p < r 2 q = floor((p+r)/2) 3 MERGE-SORT(A, p, q) 4 MERGE-SORT(A,q+1,r) 5 MERGE(A, p, q, r)
floor is the function which round down to the next lower integer.