Outline

• Finish Elementary Data Structures
• Quiz
• Binary Search Trees

Introduction

• Last day, we began talking about dynamic sets.
• We gave a set of common operations which we would like dynamics sets to support: insert, delete, search, min, max, etc.
• We then presented stack, queues, and linked lists as examples of dynamic sets and gave pseudo-code for various operations on each of these.
• We are shortly going to discuss more complicated data structures beginning with binary search trees.
• These will often make use of objects and pointers to objects. We already saw how pointers could be useful even when discussing linked lists.
• Today, we are going to start by considering how could implement pointers if we had to code them ourselves from scratch.

A Multiple-Array Representation of Objects

• One way to implement objects is with arrays.
• If we have a collection of objects, where each object has the same attributes, we can store the objects in arrays with a separate array for each attribute.
• For example, a linked list node is an object that has key, prev, next as its attributes.
• We imagine having an array for key's of all the objects we have, an array for all the next's and an array for the prev's.
• To look up the object x, we look up key[x], prev[x], next[x]. I.e., an object reference is just a common array index into the key, next, and prev arrays.
• The image above shows an example of storing a linked-list using this implementation of list nodes.

A Single-Array Representation of Objects

• The words in a computer memory are typically addressed by integers from 0 to `M - 1`.
• In many programming languages, an object occupies a contiguous set of locations in memory.
• A pointer is simply the address of the first memory location of the object, and we can address other memory locations within the object by adding an offset to the pointer.
• We can use the same strategy for implementing objects in programming environments that do not provide explicit pointer data types.
• We imagine we have an array `A` to store objects, say the linked list before.
• An object occupies a contiguous subarray `A[j..k]`. Each attribute corresponds to an offset in the range 0 to `k-j`.
• As an example for a link list node in the above diagram, the offset for key, next, and prev are 0, 1, and 2. So to look up i.prev if `i` were our pointer, we would look at A[i + 2].
• The single-array representation is flexible in that it permits objects of different lengths to be stored in the same array.
• On the other hand this makes memory management more difficult.

Allocating and Freeing Objects

• To insert a key into a dynamic set represented by a doubly linked list, we must allocate a pointer to a currently unused object in the linked-list representation.
• Thus, it is useful to manage the storage of objects not currently used in the linked-list so that one can be allocated.
• In Java, this might all be done via a garbage collector.
• Let's see how we could handle this ourselves...
• Suppose that the arrays in the multiple-array representation have length `m` and that at some moment the dynamic set contains `n le m` elements. (HW4 uses a single-array rep)
• So `m-n` objects are free. We can keep track of them using a singly-linked list called a free list.

More on the Free List

• The head of the free list is held in a global variable called free.
• When the dynamic set represented by a linked list `L` is nonempty, the free list may be intertwined with `L` as seen above.
• Each object will either be in `L` or in the free list, but not both.
• The free list behaves like a stack, the next object allocated is the last one freed.
• In the above image, going from (a) to (b) involves a call to ALLOCATE-OBJECT, setting key[4] to 25, followed by a call LIST-INSERT(L,4). (c) above follows from (b) after LIST-DELETE(L,5) and a call to FREE-OBJECT(5).
• Below is pseudo-code for allocating and freeing objects based on our earlier PUSH and POP code for stacks. Each operation is `O(1)`.

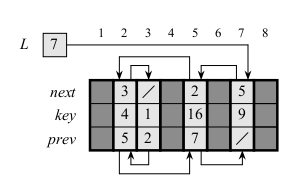
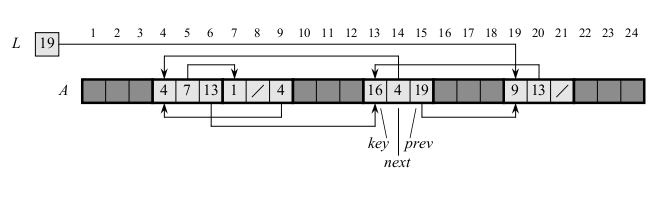
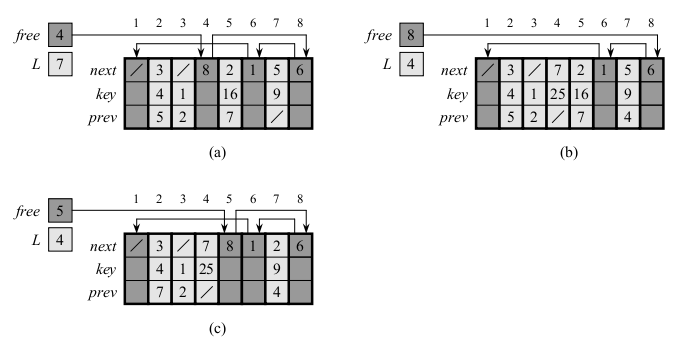
  ALLOCATE-OBJECT()
  1 if free == NIL
  2     error "out of space"
  3 else 
  4    x = free
  5    free = x.next
  6    return x
  
  FREE-OBJECT(x)
  1 x.next = free
  2 free = x 
  

Quiz (Sec 5)

Quiz (Sec 6)

Binary Search Trees

• Linked List delete and search were `Theta(n)`, where `n` is the list length in the worst case (and under reasonable assumptions, in the average case).
• We now consider using a binary search tree data structure to support the dynamic set operations.
• For complete trees this data structure will give us `Theta(log n)` time for most of the operations, in particular, search and delete.
• In the worst case, however, where the binary tree is consists of one long branch the operations are `Theta(n)`, but it can be argues that the complete tree case is more close to the typical situation.
• Let's begin by saying what a binary search tree is...

What is a Binary Search Tree?

• A binary search tree (BST) is a binary tree where each node holds a key value, and the key values satisfy the binary-search-tree (BST) property. We'll say what the BST property is below.
• Since a BST is a binary tree, we can represent it using nodes where each node holds a key value, has left and right child pointers, and has a parent pointer `p`.
• If a child or parent is missing the appropriate pointer is NIL. The root of the tree is the only node whose parent pointer is NIL.
• The binary search tree property is:

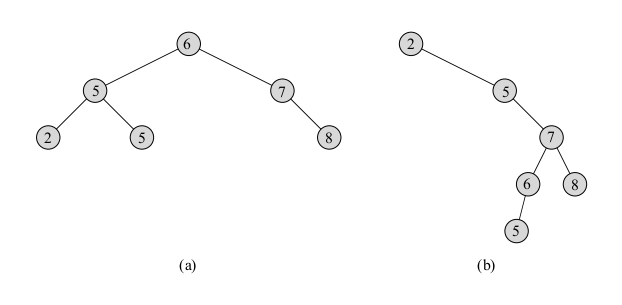
  Let `x` be a node in a binary search tree. If `y` is a node in the left subtree of `x`, then `y.key le x.key`. If `y` is a node in the right subtree of `x`, then `y.key ge x.key`.

• The diagrams above show some example binary search trees.

Tree Traversals

• The binary-search-tree property allows us to print out all the keys in a BST in sorted order by a simple recursive algorithm called an inorder tree walk
• An inorder tree walk is one in which we visit all the nodes in the left sub tree, followed by the root, followed by all the nodes in the right subtree. it is called in order because we are visiting things in order from left to right.
• Other possible tree traversals are a preorder tree walk in which we visit the root, then the left sub-tree, then the right sub-tree; and postorder tree walk where we visit the left subtree, then the right, then the root.
• Below is pseudo-code for an inorder tree walk of the tree rooted at `x` where we print the keys as we visit a node:

  INORDER-TREE-WALK(x)
  1 if x != NIL
  2    INORDER-TREE-WALK(x.left)
  3    print x.key
  4    INORDER-TREE-WALK(x.right)
  

INORDER-TREE-WALK run-time

Theorem. If `x` is the root of an `n`-node subtree, then the call INORDER-TREE-WALK(x) takes `Theta(n)` time.

Proof. Let `T(n)` denote the time taken by INORDER-TREE-WALK(x). Since INORDER-TREE-WALK visits all `n` nodes of the subtree, we have `T(n) = Omega(n)`. It remains to show that `T(n) = O(n)`.

On an empty tree INORDER-TREE-WALK takes a fixed constant `c gt 0` amount of time. So `T(0) = c`.

For `n gt 0`, suppose `x` has a `k`-node left subtree and a `n-k-1` node right subtree. The time to perform INORDER-TREE-WALK(x) is bounded by `T(n) le T(k) + T(n - k -1) + d` where `d gt 0` is the time to execute the body of INORDER-TREE-WALK(x) ignoring the recursive calls.

We use the substitution method to show that `T(n) = O(n)`, by proving that `T(n) le (c + d)n +c`. For `n = 0`, we have `(c + d)cdot 0 +c = c = T(0)`. For `n gt 0`, we have:
`T(n) le T(k) + T(n - k - 1) +d`
`qquad = ((c+d)k +c) + ((c+d)(n-k -1) + c) +d` by the induction hypothesis
`qquad = (c+d)n + c - (c + d) + c + d`
`qquad = (c+d)n +c`, so the induction holds, completing the proof. QED.