Quicksort

CS146

Chris Pollett

Mar 3, 2014

Outline

Description of Quicksort
Quiz
Performance of Quicksort

Introduction

Last week, we looked at heaps, heapsort, and priority queues.
Today, we will consider another sorting algorithm known as quicksort.
In the worst case, this algorithm runs in `Theta(n^2)`, but in the average case it runs in `Theta(n log n)`
Moreover, the constants of quicksort in the average case are better than that of heapsort so it tends to be used more in practice.

Description of Quicksort

Like mergesort, quicksort is a divide-and-conquer algorithm.
Here is the three-step divide-and-conquer process for sorting a subarray `A[p..r]` with quicksort:

Divide
Partition the array `A[p..r]` into two (possibly empty) subarrays `A[p..q-1]` and `A[q+1, r]` such that each element of `A[p..q-1]` is less than or equal to `A[q]`, which is in turn, less than or equal to each element of `A[q+1, r]`. Compute the index `q` as part of this partitioning procedure.

Conquer
Sort the two subarrays `A[p..q-1]` and `A[q+1, r]` by recursive calls to quicksort.

Combine
Because the subarrays are already sorted, no work is needed to combine them, the entire array `A[p..r]` is now sorted.

A procedure to implement the above is:

QUICKSORT(A, p, r)
1 if p < r
2     q = PARTITION(A, p, r)
3     QUICKSORT(A, p, q - 1)
4     QUICKSORT(A, q + 1, r)

Partitioning the Array

Let's look at a first way we might go about implementing the partition procedure which rearranges the subarray `A[p..r]` in place:

PARTITION(A, p, r)
1 x = A[r]
2 i = p - 1
3 for j = p to r - 1
4     if A[j] <= x
5         i = i + 1
6         exchange A[i] with A[j]
7 exchange A[i+1] with A[r]
8 return i + 1

Example

The idea is `j` is cycling over items to consider
Element of `A[p..j]` with index positions less than `i` will be less than or equal to `x = A[r]`. So `A[i] > x`, but everything to its left will be less than or equal to `x`.
If an element `A[j]` is less than `x` we just bump `i` by `1`. By swapping `A[j]` and `A[i]` we will have everything to the left of `A[i+1]` is again less than or equal to `x` and `A[j] > x`.
We see this kind of swapping happening in step (e) above.
When we get to the end of the array location `A[i+1]`will have a value bigger than `A[r]` so it makes sense to swap these two items.

PARTITION loop invariant

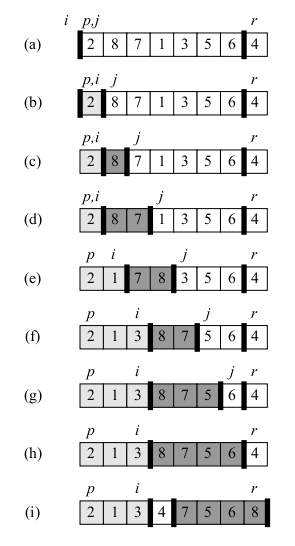
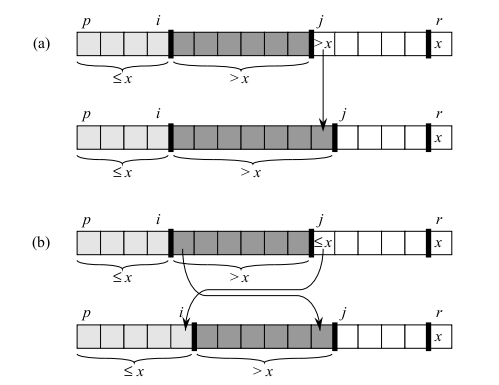
Four ranges of values that appear in PARTITION procedure

Theorem. The partition function for quicksort satisfies the following loop invariant:

At the beginning of each iteration of the loop of lines 3-6, for any array index `k`

If `p le k le i`, then `A[k] le x`

If `i+1 le k le j-1` then `A[k] > x`

If `k=r`, then `A[k] = x`

Proof. We need to show the three properties of loop invarants:

Initialization: Prior to the first iteration of the loop, `i = p - 1` and `j = p`. Because no values lie between `p` and `i` and no values lie between `i+1` and `j-1` the first two conditions of the loop invariant are trivially satisfied. The assignment in line 1 ensures the third condition.
Maintenance: There are two cases depending on the outcome of of the test in line 4. If `A[j] > x` the only action in the loop is to increment `j`. After `j` is incremented, condition 2 holds for `A[j-1]` and all other entries remain unchanged. (See case (a) of the image above). If `A[j] le x`, the loop increments `i`, swaps `A[i]` and `A[j]`, and then increments `j`. Because of the swap, we now have that `A[i] le x`, and condition 1. Similarly, we also have that `A[j-1] > x`, since the item that was swapped into `A[j-1]` is by the loop invariant greater than `x`. (See case (b) above.)
Termination: At termination, `j = r`. Therefore, every entry in the array is in one of the three sets described by the invariant, and we have partitioned the values in the array into three sets: those less than or equal to x, those greater than `x`, and a singleton set containing `x`.

In the termination setting, the exchange in line 7 puts `x` into the correct place in the partitioned array and the return statement gives the position of the partition in the array so it can be used by quicksort.

Since partition involves only a single loop and otherwise statements each involving constant work, its run time will be `Theta(n)`, where `n = r - p +1`.

Quiz (Sec 5)

Which of the following statements is true?

If a heap has the max-heap property then `A[Pa\r\ent(i)] le A[i]` for all nodes `i` in the heap.
The Master Theorem can be applied to the recurrence `T(n) = 4T(n/4) + sqrt(n)`.
We used a probabilistic argument to show BUILD-MAX-HEAP(A) was an `Omega(n^2)` algorithm where `n = A.`length.

Quiz (Sec 6)

Which of the following statements is true?

If `T(n) = 128 T(n/2) + 2^n`, then `T(n) = Theta(2^n)`.
The master theorem can be applied to the recurrence `T(n) = (T(n/2))^2 + 1`.
Inserting a new element into a heap require `Omega(n)` time where `n=A.`length.

Performance of Quicksort

The running time of quicksort depends on whether the partitioning is balanced or not.
If the partitioning steps performed are balanced the algorithm runs asymptotically as fast as merge sort.
Let's look at the different possibilities in more detail...

Worst-case Partitioning

The worst-case behavior occurs when the partitioning routine produces one subproblem with `n-1` elements and one with `0` elements.
This happens if the array is already sorted.
Let us assume that this unbalanced partitioning arises in each recursive call.
The partitioning cost is `Theta(n)`. Since the recursive call on an array of size `0` just returns, `T(0) = Theta(1)`.
So the recurrence for the running time is:
`T(n) = T(n-1) +T(0) + Theta(n)`
`=T(n-1) + Theta(n)`
Using the substitution method we can check that this gives `T(n) = Theta(n^2)`.

Best-case Partitioning

In the best case, PARTITION produces two subproblems each of size no more than `n/2`.
So the recurrence we get is
`T(n) = 2T(n/2) + Theta(n)`.
By case 2 of the master theorem, this recurrence has solution `T(n) = Theta(n log n)`.