There are situations where two objects are composed to appear as a single object. One object, called the handle, manages the interface, while another object called the body provides the application logic.

Shared objects arise in several contexts:

1. An object may be too large to be copied such as a CAD-CAM model of a jumbo jet or the text of a long document,

2. having multiple instances of an object may lead to too many objects. For example, if we want to represent individual characters in a document as objects (bodies are called flyweights in this context),

3. the object may represent a unique resource such as a file, communication chanel, or remote server,

4. or the object may be stateless, hence multiple instances aren't necessary such as non-mutable strings.

These objects can be shared by providing clients with unique proxy objects representing the shared object. In this case the shared object is the body, while the proxies are handles.

In distributed client-server applications client and server objects reside on different machines connected by a network. We want to shield client objects from the details of remote communication (sockets, IP addresses, ports, creating connections, etc.) and instead allow clients to communicate with server objects (the body) using ordinary method invocation (RMI). We can achieve this by introducing a client-side proxy (the handle) that encapsulates the low-level communication details.

Sometimes the responsibilities of an object naturally divide into two categorties. In these situations it is sometimes a good idea to separate these responsibilities into two associated objects. In the orthodox canonical form, for example, the handle performs memory management duties whiule the body implements application logic.

One solution is to introduce a handle as an adapter and a body as the adaptee.

There are two competing reuse/extension mechanisms in object oriented programming: inheritance and delegation.

Sometimes inheritance is called white-box reuse because the public and protected members of the base class are visible to the derived class. Delegation is called black-box reuse because the protected members of the delegate are not visible to the delegator.

Several idioms and design patterns use a handle object as the interface and body objects as implementors: strategy, state, visitor, bridge, and envelope-letter to name a few.

How do we integrate objects from other languages into a C++ program? Naturally clients want to be shielded from the syntax and semantics of the foreign object. The idea is to encapsulate a reference to the foreign object (the body) in a C++ object called a wrapper (the handle), which also encapsulates the syntax and semantics of the body. Clients only see and use the wrapper. This technique is used (with limited success) in the MFC framework. Before the framework Windows applications were built out of C "objects" called windows. MFC provides C++ wrapper objects that (partially) encapsulate references to window objects. (Unfortunately, MFC uses the term "handle" to refer to a wrapper's "reference" to the window.)

We can take this idea one step further by allowing the body to be an ordinary C-style data structure such as a linked list or a tree. In this case the wrapper manages access to the data structure and provides memory management.

Assume we create two handle-body pairs:

The picture in memory looks like this:

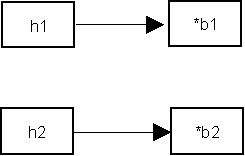
Now assume we change our minds and reassign h2 to be like h1:

The default assignment algorithm in C++ is called member-wise copy. Each field of h1 is copied to the corresponding field of h2, including the pointer b1. The new picture looks like this:

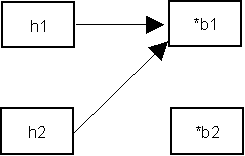
There are two problems. First, we have a memory leak because *b2 was not properly deallocated (remember, b2 was encapsulated by h2, so there are no more active references to *b2.) Second, we have a potential aliasing problem because h2 and h1 both reference the same body. Changes to the body made through h2 will be reflected in h1.

The soulution is to redefine the assignment operator:

The picture now looks like this:

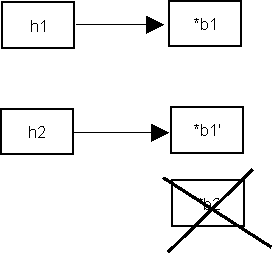
Handles can also be copied by copy constructors, again the default algorithm is member-wise copy, hence we must redefine the copy constructor:

(Whenever we define a constructor, we must also define a default constructor, otherwise we may loose the C++ provided default constructor, which is used to initialize arrays of handles.)

We must also provide a destructor that automatically deallocates the body when the handle is deallocated:

The copy() and free() functions are private member functions that encapsulate the details of coying and deleting bodies. The new declarationg of the Handle class looks like this:

The members shown in bold face are required for every handle class. Coplien refers to these members collectively as the orthodox canonical form (OCF).

C pointers are dangerous creatures. Programmers are always dereferencing null pointers, producing the infamous "core dump" message and crashing the program, or programmers change the value of a pointer, forgetting to delete the memory it formerly pointed at, creating a memory leak.

One solution is to provide programmers with smart pointers that automatically solve these problems. (In this context C pointers are often called "dumb pointers.") A smart pointer encapsulates and manages a dumb pointer, so users never need to worry about new and delete. Here are some sample programs using smart pointers.

We'll need this to get smart pointers:

Test1 expects a C pointer, but we can pass it smart pointer. Test2 expects a smart pointer but we can pass it a C pointer:

Notice that main never calls new or delete for smart pointers:

In this demo we create smart pointers to Person objects:

Main() creates four smart pointers to persons, then calls Person::print() using the -> operator:

A smart pointer encapsulates and manages a dumb pointer. In this context the smart pointer is the handle and the dumb pointer is the body. We'll need to use orthodox canonical form. Also, smart pointer will need to be a template:

Dereferencing a null smart pointer prints a useful error message, then gracefully terminates the program:

OCF assignment is always the same:

The copy member function automatically allocates memory:

smart arrays, safe arrays, dynamic arrays, dynamic linear lists

Inserting and deleting elements from a linked list is efficient, but accessing random elements is not since the cursor must be reset to the start of the list, then moved step by step to the desired position.

Using a C array to implement a random access store is unsafe since no array bounds checking is done, and changing the size of a C array is impossible. While changing the size of a C pointer to an array is possible, it's awkward, and still no array bounds checking is done.

A vector encapsulates and manages a C array on the heap. An overloaded [] operator automatically checks index bounds.

A vector encapsulates and manages a pointer to an array on the heap, so we'll need to use orthodox canonical form. Naturally, vector will need to be a template.

The basic constructor automatically allocates memory:

As always:

The copy member function allocates a new array the size of v.vals, then performs a component-wise copy:

The subscript operator performs index bounds checking:

If necessary, grow() creates a new array, BLOCK_SIZE storables larger than the old array, copies the old array into the new array, then deletes the old array. Note: this is more efficient than doubling the size of the old array.

New items can be added to a vector using insert or push_back. Note that push_back is much more efficient, because insert must move move as many as _size elements.

Erase is also inefficient, because it may need to move up to _size elements. It's better to replace items using [] rather than erase them.

A little print utility:

Reference counting

Orthodox canonical form can be dangerous if the handle ends up deleting a body that is referenced by other handles. This is possible when the body is a shared object. As a general rule, an object should only delete objects it creates. But what if no other objects are referencing the body? How would the handle know this?

The body can keep count of the number of handles that reference it. Each new handle that references the body should increment this count. Handles should decrement the count just before they disappear. The handle that decrements the count to zero should delete the body.

Only handles can construct bodies, because the body constructors are private:

The handle is as above, but the non-copy constructors must allocate a new body and set its reference count to 1:

The free method first decrements the count. If the count has reached 0, then the body must be deleted:

The copy method increments the count, that attaches itself to the body of h:

As an example, we might implement safe, non-mutable strings using the handle body idiom. A character in a non-mutable string can't be altered. For example, to create the string "cat" from "bat", a new string needs to be created. Java strings are non-mutable.

Here are the includes we need:

StringBody encapsulates a C++ string and provides some basic access services:

The String class encapsulates a pointer to a StringBody and implements orthodox canonical form:

Implementations of copy and free are separated from their declarations:

Here's a little test harness:

Clients often regard the lower levels of an inheritance hierarchy as details they don't want to know about. Clients want to deal with generic abstractions like curves and surfaces rather than technicalities like conic sections, Bezier splines, and revolutes.

C++ already provides abstract classes that allow programmers to seperate interface from implementation, but what happens when several generic objects of the same type can have different implementations. For example, a complex number can be represented in rectangular form as a+bi or in polar form as re^iq. How do we allow both representations to coexist while the user is blissfully ignorant of which of his complex numbers use polar form and which use rectangular form?

When the services of a body specialize the services of the handle, we call the body a letter and the handle an envelope. In this case the Handle-Body idiom is called the Envelope-Letter idiom. (Names like "Envelope-Letter" and "Orthodox Canonical Form" come from James Coplien's book Advanced C++ Programming Styles and Idioms.)

The envelope defines a generic type (like curve, surface, or complex number). The envelope encapsulates a pointer to a particular representation, called the letter (like conic section, revolute, or polar). Envelope constructors and factory methods deduce the type of letter to create from their parameters and contexts. Envelope member functions are always virtual and always delegate work to member functions of the same name in the letter class. Thus, the typing system does most of the work for us.

There are many types of numbers: integer, rational, real, and complex numbers. Although all types of numbers may be needed by our clients, our clients may only be interested in using generic numbers, leaving the representation details to us on a case by case basis.

We can use the Envelope-Letter idiom to implement the Number class. In this case Number is the envelope class, while Rational, Complex, Real, and Integer are the letter classes:

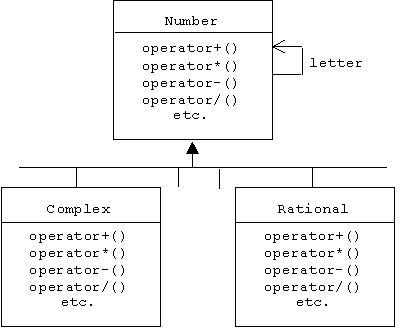
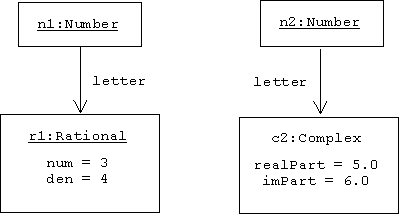
The interesting feature of the Envelope-Letter idiom is that the letter classes inherits from the envelope class, while the envelope class delegates to the letter class. Here's an object diagram showing the first two numbers created in the example above:

Class derivation in C++ blurs the distinction between specialization and extension. If class A extends class B, then instances of A contain the attributes from B extended by the attributes from A. An instance of A is a single object, probably allocated in a contiguous block of memory.

If class C specializes class B, then x, an instance of A, contains a reference to y, a seperate instance of B. y represents a generalization of x and x represents a specialization of y. Sometimes we want x, sometimes we want y.

In the Envelope-Letter idiom we have both specialization and extension. Let's name the instance of Rational in the object diagram r1. Although r1 and n1 are distinct objects in the computer's memory, r1 is a logical specialization of n1, and n1 is a logical generalization of r1. Of course Rational extends Number, so number attributes, if any, can be found inside of r1. As such, we can regard r1 as an instance of Number with some added attributes. We can retype r1 as a Number with a cast. Let n = (Number) r1. While some might claim n to be the C++ generalization of r1, it is unrelated to the logical generalization, n1.

Assume n1 and n2 are as in the example above. Assume Rational(*(n1.letter)) = r1 is actually an instance of Rational, and Complex(*(n2.letter)) = c2, an instance of Complex. We use the C++ typing system to delegate the calculation of n1 + n2 to c2 + r1:

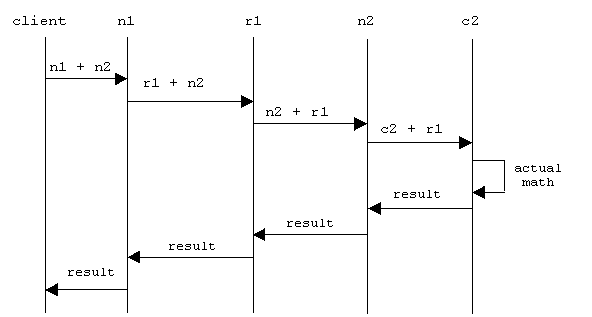
Note that the actual addition can only be preformed in c2 + r1, where the specific representation of c2 and r1 is known. Also note that our addition operators are not commutative. We use the argument order to determine which variant to call.

The implementation isn't difficult, but involves writing a lot of code. Most of the member functions merely delegate to the corresponding member functions of the letter. To do this, it is important that these functions are virtual and that letter is a pointer. Otherwise, infinite recursions result.

You'll need some declarations at the top of number.h:

The bad news is that each arithmetic operation (+, *, /, -) requires five member functions in the Number base class. (Total = 4 * 5 = 20.) One to be used when *this is the first operand, the others to be used when *this is the second operand. In this case the parameter type tells us the letter type of the first argument. The good news is that the code of each of the five member functions is exactly the same: return *letter + n; This is because operator+ is heavily overloaded in the derived classes.

Note the protected constructor expecting a parameter of type Token, where Token is the bogus empty class defined earlier. This is the constructor used by the derived classes, but never other clients, to create an extension (i.e. not generalization) of type Number. Using the other constructors would result in an infinite regress of specializations creating generalizations, creating specializations, etc.

Each derived class must over ride the 4 * 5 = 20 virtual arithmetic operators defined in the Number base class. (There are four derived classes, which means 4 * 20 = 80 member functions! This is a bit much, but it is still a great exercise in C++. Can you think of any short cuts using macros, templates, etc.?)

The other classes are similar. Rational encapsulates two integers representing the numerator and denominator, Real encapsulates a double, and Integer encapsulates an int:

Implementation of Number constructors must be seperated from their declaration, because at the time of declaration, we didn't know what type of derived class constructors would be available to us. For example, the Number constructor receiving two ints, n and d, must define letter = new Rational(n, d).

Recall that the actual mathematics can only be implemented when the derived types of both arguments are known. Here's an example. At this point we know the implicit parameter is complex and the explicit parameter is rational. In this case we must transform the rational x into a double by dividing its numerator by its denominator. The result, x2, is added to the real part of the implicit parameter. The answer is a new complex number made this sum and the imaginary part of the implicit parameter. (Adding a real, rational, or int to a complex number doesn't effect its imaginary part.)

Complete the implementation of generic numbers. You don't have to implement division and subtraction, but do finish addition and multiplication.

Create a test harness (main) to test your implementation. The test harness should only refer to the Number type, never the derived types.

1. Supply a reader for the Number class. A reader is just a global function of the form:

Use some of the tricks used in utils.cpp to determine from the contents of is what type of letter to create.

2. The Number class should use orthodox canonical form to manage its letter pointer, but how can the copy member function be implemented:

if the derived type of the letter is unknown? One ide is to make the copy function virtual, and over ride it in the derived classes. Then Number::copy simply calls n.letter->copy().

3. For testing purposes, don't worry about reducing rational numbers. If you have time, you should reduce rational numbers in the rational number constructors and readers. Here's a useful member function that reduces and normalizes its rational implicit parameter:

gcd() is an efficient tail recursion that uses an Euclidean algorithm to find the greatest common divisor of n and m:

sign() returns 1 if 0 <= n and –1 otherwise:

4. It might simplify things to supply constructors and overloaded casting operators between our derived number types and the corresponding C++ types. For example, we could define

Then Complex::operator+ is simply:

We don't even need the explicit cast. C++ will provide it for us automatically!

5. The low level arithmetic functions should be improved so they return the simplest type answer possible. For example (3.0 + 4.0i) * (3.0 + -4.0i) should return the integer 25.