A Mathematical Example

Associations and Links

Assume A and B are sets:

A = { a1, a2, a3 }

B = { b1, b2, b3 }

 Assume R is some relationship between A, and B, i.e., R is a subset of A x B: R = { (a1, b1), (a1, b2), (a2, b1), (a2, b3), (a3, b2), (a3, b3) } We might represent this situation with the following UML class diagram:

Note: This doesn't quite work, because it doesn't say if R is a subset of A x B or of B x A. If we attach roles, then we can make this distinction:

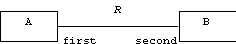
An object diagram looks like this:

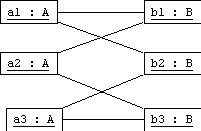
The connecting lines are called links. These will probably be represented by pointers in C++.

If we further assume the relationship is bi-directional with a 1 to 2 multiplicity, then here is how we might represent it in C++:

class A
{
    B* second1, second2;
    // etc.
};

class B
{
    A* first;
    // etc.
};

 Association Classes

If the links are important to our application, then we might want to represent them as objects instead of pointers. Link objects are instances of association classes.

Note: Mathematicians don't distinguish between pairs and elements nor between relationships and sets. The pairs (a1, b1), (a1, b2), etc. are viewed as mathematical objects, just as the elements a1, b1, b2, etc, and the relationship R is viewed as a mathematical set just as A and B.

The UML notation for an association class is:

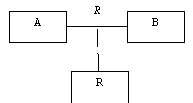
Now links are link objects:

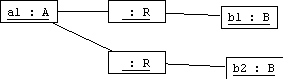
Power Types (Meta-Level Classes)

Assume U is the universe of all objects:

U = { a1, a2, a3, b1, b2, b3 } Then A and B are subsets of U.

The power set of U, P(U) is the set of all subsets of U:

P(U) = { {}, {a1}, {a1, a2}, {a1, b1}, ..., U } Clearly A and B are elements of P(U). (Q: What is the cardinality P(U)?).

Subsets of P(U) are called power sets. For example:

AAA = all subsets of U that don't contain b1, b2, or b3.

BBB = all subsets of U containing b3.

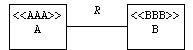
 Clearly A is an element of AAA while B is an element of BBB. If AAA and BBB were important categories in our application, then we might represent them as stereotypes:

We can also introduce P(U) as a meta-level class. Every base-level class points to the object in P(U) that represents it:

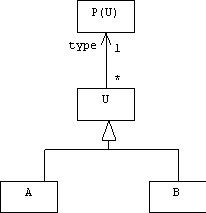
The association in the diagram indicate that it is possible to ask instances of A and B what their types are.

class P(U) { ... };

class U
{
protected:
    P(U)* type;
    // etc.
};

class A: public U { ... };
class B: public U { ... };

 Notice that the type of A, the subset of U is A the element of P(U), and the type of B the subset of U is B the element of P(U). In other words, A has two representations in our model, there's the class A and the object A. Thus, it's possible to query an element of A, say a1, about its type: if (a1.type == A) ... This is especially useful if a1 is a reference that was originally declared as an instance of U: U a1 = new A; // in Java