Finite State Machines
Definition
A finite state machine (FSM) is a directed graph in which nodes represents the possible states of some type of machine and arrows represent transitions from one state to another. Each transition is labeled by an event that causes the machine to change from the source state to the destination state. The initial state is indicated by a transition without a source state. A final state is indicated by a transition without a destination state:

In a sequential FSM only one state is active at any given time. In a concurrent FSM several states may be active simultaneously.
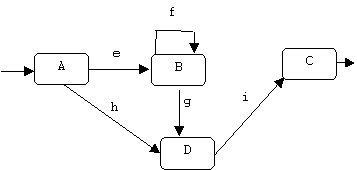
In our example the states are A, B, C, and D. A is the initial state, C is the final state. The events are e, f, g, h, and i.
If M is an FSM, and w is a sequence of events, then M(w) = the sequence of states M passes through while processing w, assuming M started in the initial state. We say M accepts w if M(w) ends in a final state.
For example, M accepts the string affgi, because:
M(effgi) = ABBBDC
ends in state C, which is a final state.
Every machine has an implicit ERROR state that it transitions to if an unspecified event occurs.
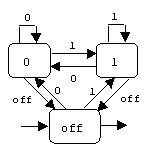
Example
A flip-flop is a simple example of an FSM that remembers the last 0 or 1 event:
Applications
Recognizing Regular Languages
Let S be a finite set of symbols or characters. Let S* be the set of all strings over S. Subsets of S are called languages over S. Assume A and B are languages over S, then define:
A + B = A U B // union
AB = { uv | u in A and v in B } // concatenation
A0 = { "" } // "" = the empty string
A1 = A
An = AAn-1
A* = A0 + A1 + ... + An + ... // Kleene star
FINITE(S) = all finite languages over S // this includes {}, the empty language
REGULAR(S) = the smallest family of languages over S containing FINITE(S) and closed under union, concatenation, and Kleene star. Intuitively, a language is regular if it is simple to define.
Theorem: If M is a FSM, let LM = { w | M accepts w }. Then LM is a regular language. Conversely, if A is a regular language, then there is an FSM MA, such that MA accepts strings if and only if they are in A. (Here we interpret the members of S as event).
Example
The set of all legal numbers forms a regular language which is recognized by the following FSM:
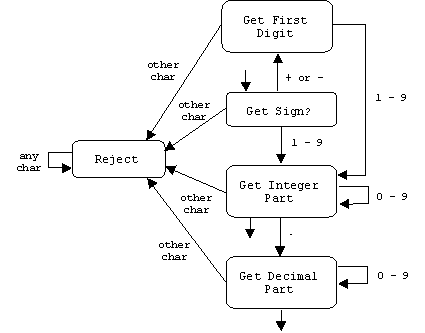
We can use this FSM to generate a scanner algorithm for recognizing legal numbers.
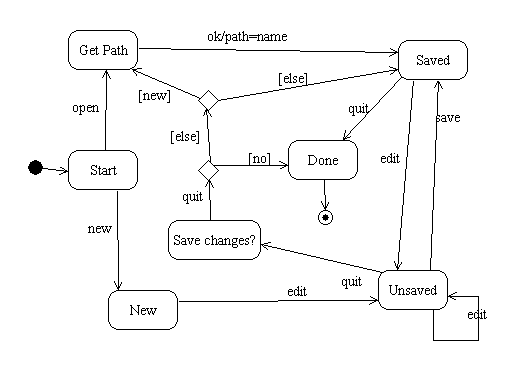
Lifecycle Models
An FSM can be used to represent the lifecycle of an object:
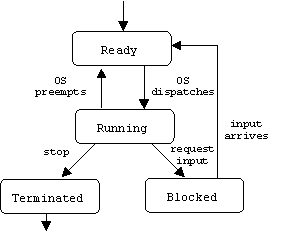
Specifying Workflows
An FSM can be used to represent a process, protocol, or workflow. In this case the states represent activities and transitions are often not labeled by events. This is because the event is implicitly understood to be the completion of the activity represented by the source state. We call such FSMs activity diagrams.
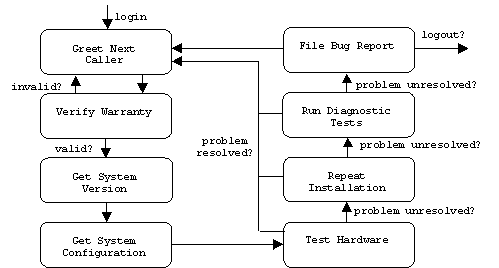
Elaborating Use Cases
A use case can be interpreted as an FSM. In this case events are actor messages. Transitions may cause messages to be sent from the system to the actor and may cause certain internal actions to be performed.
Example:
A computer game allows players to navigate a maze:
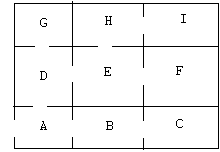
The goal of the game is to navigate from room A to room I. The basic messages the actor may send are up, down, right, and left:
S = { U, D, L, R }
The basic messages the game sends are:
R = {A, B, C, D, E, F, G, H, I, ERROR}
We can identify the use case "play game" with the FSM M:
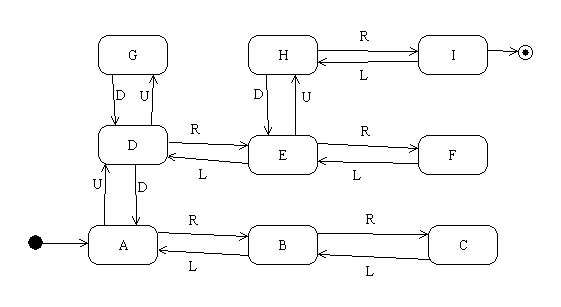
For example:
FM(UDRLURUR) = ADABADEHI
which, if this is the actor's complete message sequence, is a win.
Events
UML specifies four types of events:
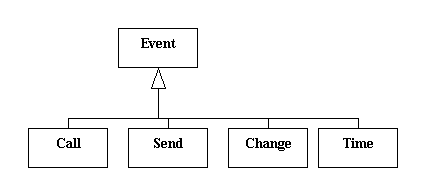
An event can have:
1. arguments
2. conditions
3. actions
For example, an ATM machine may an edit box where users enter an amount, and a withdraw and deposit button.
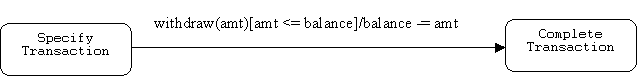
Transitions may or may not trigger state changes. In some cases we may regard a state as a sub FSM. Transitions from the state to itself can be regarded as transitions in this sub FSM.
Branching Transitions
A transition may contain branches labeled by guards:
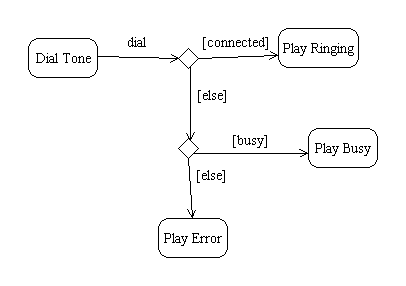
The opposite of a branch is a merge:
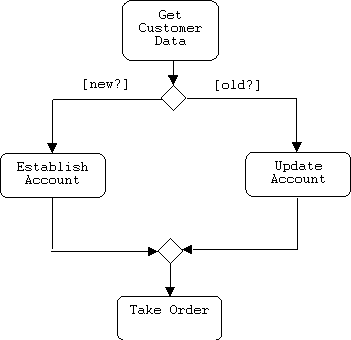
Forks and Joins
Forks and joins show parallel state activations in a concurrent FSM. These parallel paths are called swimlanes.
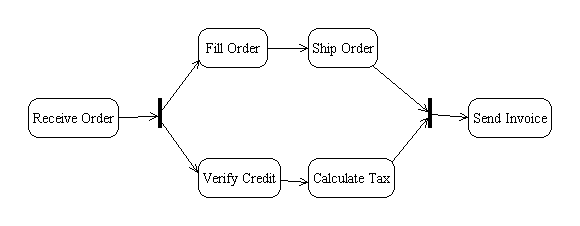
Example
Here's a use-case FSM for a simple calculator that allows addition and multiplication of unsigned integers:
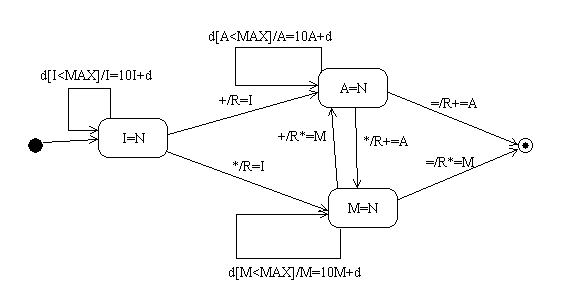
Example
Here's an FSM that shows for the document editor discussed earlier: