Design Principles

Modularity and Abstraction

The Modulariy Principle:

Systems should be built from cohesive, loosely coupled classes.

The Abstraction Principle:

The interface of a class should be independent of its implementation.

A cohesive class has a unified purpose, while loose coupling implies dependencies on other classes are minimized. Taken together, this makes a class easier to reuse, replace, and understand.

The abstraction principle implies that the external function or purpose of a class (the class' interface) should be separated from its internal structure (the class' implementation). A dependency on such a class is only a dependency on its public interface, not its private implementation. This frees clients from the need to understand implementation details, while implementers are free to modify the implementation without the fear of breaking client code.

Cohesion

The methods of a cohesive class work together to achieve a common goal. Classes that try to do too many marginally related tasks are difficult to understand, reuse, and maintain.

W we can identify several common "degrees" of cohesiveness. At the low end of our spectrum is coincidental cohesion. A class exhibits coincidental cohesion if the tasks its methods perform are totally unrelated:

class MyFuns {
void initPrinter() { ... }
double calcInterest() { ... }
Date getDate() { ... }
}

The next step up from coincidental cohesion is logical cohesion. A class exhibits logical cohesion if the tasks its methods perform are conceptually related. For example, the methods of the following class are related by the mathematical concept of area:

class AreaFuns {
double circleArea() { ... }
double rectangleArea() { ... }
double triangleArea() { ... }
}

A logically cohesive class also exhibits temporal cohesion if the tasks its methods perform are invoked at or near the same time. For example, the methods of the following class are related by the device initialization concept, and they are all invoked at system boot time:

class InitFuns {
void initDisk() { ... }
void initPrinter() { ... }
void initMonitor() { ... }
}

One reason why coincidental, logical, and temporal cohesion are at the low end of our cohesion scale is because instances of such classes are unrelated to objects in the application domain. For example, suppose x and y are instances of the InitFuns class:

InitFuns x = InitFuns(), y = new InitFuns();

How can we interpret x, and y? What do they represent? How are they different?

A class exhibits procedural cohesion, the next step up in our cohesion scale, if the tasks its methods perform are steps in the same application domain process. For example, if the application domain is a kitchen, then cake making is an important application domain process. Each cake we bake is the product of an instance of a MakeCake class:

class MakeCake {
void addIngredients() { ... }
void mix() { ... }
void bake() { ... }
}

A class exhibits informational cohesion if the tasks its methods perform operate on the same information or data. In object oriented programming this information would be the information contained in the variables of an object.

For example, the Airplane class exhibits informational cohesion because its methods all work on the same information: the speed and altitude of some airplane object.

class Airplane {
double speed, altitude;
void takeoff() { ... }
void fly() { ... }
void land() { ... }
}

Note that the informational cohesion of this class is ruined if we add a method for computing taxes or browsing web pages.

Measuring Cohesion

Chidamber & Kemerer provide a metric for measuring a module's lack of cohesion (LCOM1). There are several minor improvements on this metric (LCOM2 and LCOM3).

The basic idea is to measure how far a class is from information cohesion by measuring the degree to which the methods share the fields.

LCOM1

In a method coupling graph for a class C-- MCG(C)-- nodes are methods. Two nodes are connected by an undirected edge if they both reference the same field. In fact, the edge can be labeled by the number of common attributes the methods reference.

(a) Draw MCG(Test) where Test is the following class:

class Test {
int a, x, y, z;
void m1() {
System.out.println(x);
System.out.println(y);
}
void m2() {
System.out.println(y);
System.out.println(z);
}
void m3() {
System.out.println(x);
System.out.println(z);
}
void m4() {
System.out.println(a);
}
void m5() {
System.out.println(a);
}
}

LCOM1(C) is the maximum possible number of edges in MGC(C) less the actual number of edges:

LCOM1(C) = choose(n, 2) - e

where:

n = # of nodes in MCG(C) = # of methods in C
choose(n, 2) = n * (n - 1) / 2 = maximum # of possible edges
e = # of edges in MCG(C)

(b) Compute LCOM1(Test).

(c) Assume a class C has 10 methods. What are the possible values of LCOM1(C)?

(d) Under what conditions does LCOM1(C) = 0?

LCOM2 and LCOM3

In a method-attribute graph for a class C-- MAG(C)-- nodes are methods and attributes (fields). A directed edge connects a method node to an attribute node if the method references the attribute.

(e) Draw MAG(Test).

If every method of class C references every field of C, then MAG(C) would contain n*a edges, where:

n = # of methods
a = # of attributes

Assume:

e = # of edges in MAG(C)

Then e/(n*a) measures C's degree of cohesion. Since this number is <= 1, then 1 minus this number measures C's lack of cohesion:

LCOM2(C) = 1 - e/(n * a)

(f) Compute LCOM2(Test).

Finally:

LCOM3(C) = n/(n - 1) * LCOM2(C) = (n - e/a)/(n - 1)

(g) Compute LCOM3(Test).

(h) Prove 0 <= LCOM2(C) <= 1

(i) Prove 0 <= LCOM3(C) <= 2

(j) What action would you recommend if LCOM3(C) > 1?

Coupling

Dependency

Class A depends on a class B if changes to B could require changes to A. Dependency is a transitive relationship:

1. A depends on A
2. If A depends on B and B depends on C, then A depends on C

Also:

3. If A references B, then A depends on B

A references B

Class A reference class B explicitly if B appears in the declaration of A. For example, A might extend B or have a field of type B or have a method that references B. A method references B if the method has a parameter or local variable of type B:

class A extends B {
private B field1;
private B[] field2;
public void meth1(B param1) { ... }
public void meth2() {
B local1;
...
}
}

It is also possible for A to implicitly reference B. This means A uses an object of type B without naming it. For example:

class B {
public void foo() { ... }
}

class C {
private B field;
public B getField() { return field; }
}

class A {
private C c;
public void meth() {
c.getField().foo();
}
}

In general, implicit references should be avoided. For example here's a slight improvement:

class A {
private C c;
public void meth() {
B b = c.getField();
b.foo();
}
}

Better still:

class A {
C c;
void meth() {
c.foo();
}
}

Then modify C to hide its field:

class C {
B field;
//B getField() { return field; }
void foo() { field.foo(); }
}

Dependency Graphs

Let P be a program or a package. In the dependency graph of P—DG(P)—the nodes are the classes in P. A (dashed) arrow connects node A to node B if class A references class B.

A class diagram for P approximates DG(P) in the sense that an association arrow or generalization arrow connecting A to B indicates that A references B. Of course A could reference B in other more subtle ways that aren't shown in a class diagram.

Coupling Metrics

Assume A is a class in program or package P.

clients(A) = the set of all classes in P that reference A.
providers(A) = the set of all classes in P that A references.

We are often only interested in the number of classes in each of these sets:

#clients(A) = the size of clients(A.)
#providers(A) = the size of providers of A.

A responsible class has many clients. A stable class has few providers. A general goal is that responsible classes should also be stable. If a class has many providers and many clients, then a change to any provider could propagate to all of the clients.

We could measure the responsibility and instability of a class A relative to a package or program P more formally as:

responsibity(A) = #clients(A)/#P
instability(A) = #providers(A)/#P

where:

#P = the number of classes in P

(a) Compute responsibility(C) and instability(C) for each class C in P, where P is the following program:

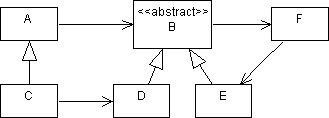
Coupling Degree

The coupling degree is a measure of the intimacy of a dependency between two classes. Based on Hitz & Montazeri we proposed the following measure of coupling degree:

couplingDegree(A, B) =
   (instability(B) + access(A, B) + scope(A, B))/3

Where:

access(A, B) = # B members A references/# B members

scope(A, B) = # A members that reference B/# A members

For example, assume A and B belong to a package P that contains ten classes: A – J. Here's the declaration of B:

class B {
private C c;
private D d;
public void service1() { ... }
public void service2() { ... }
void service3() { ... }
protected void serivce4() { ... }
private void service5() { ... }
}

Furthermore, assume B references classes C and D only.

Here's the declaration of A:

class A {
private B b = new B();
public void meth1() {
B temp = new B();
b.service1();
temp.service2();
}
public void meth2() {
b.service3();
}
public void meth3() {
String msg = "Hello";
System.out.println(msg);
}
}

Clearly A depends on B. We can compute the intimacy of this coupling as follows:

cplDeg(A, B) =
(instability(B) + access(A, B) + scope(A, B))/3

Where:

instability(B) = 2/10 (P has 10 classes but B only references 2)
access(A, B) = 3/7 (B has 7 members but A only uses 3)
scope(A, B) = 3/4 (A has 4 members but only 3 use B)

Adding and dividing we get:

(2/10 + 3/7 + 3/4)/3 = (.20 + .43 + .75)/3 = .46

Project: The Design Analyzer

There are many tools that will compute various design metrics for a given program. In this project we will develop our own.