6. Aggregation

Part-Whole or Meronymic Relationships

Taxonomic hierarchies (such as those arising in Biology) are easy to represent in object-oriented models using generalization. Less familiar are partonomic or meronymic hierarchies. These are hierarchies built using the relationship:

A is part of B

Unfortunately, this simple sounding relationships has three dimensions to it that yield at least six different meanings. The three dimensions are:

C = configurational = parts have a functional/structural relationship to each other or whole

H = homogeneous = parts same kind as whole

I = invariance = parts can be separated from the whole

Notation: We will use CHI to indicate a relationship that is configurational and invariant, but not homogeneous.

Assembly/Component Aggregation (CHI)

An engine is part of a car.
A piston is part of an engine.

Container/Member Aggregation (CHI)

A car is part of a fleet of cars.

Other types of aggregation

Mixture/Ingredient Aggregation (CHI)

Flour is a part of a loaf of bread.

Metal is part of a car.

Whole/Portion Aggregation (CHI)

A slice of bread is part of a loaf of bread.

Place/Region Aggregation (CHI)

California is part of the USA

Partnership/Partner (CHI)

Laurel is part of Laurel and Hardy

Non Part-Whole Relationships

Topological Inclusion

the customer is in the store

Classification Inclusion (is-a)

Moby dick is a book

Attribution

Smith is 5 feet tall

Attachment

Feet are attached to legs

Ownership

Smith owns a bicycle

Transitivity Problem

Assume we represent the relationship X is part of Y by:

X partOf Y

Assume:

X partOf Y and Y partOf Z

Can we infer:

X partOf Z

In other words, is the partOf relationship transitive?

Generally, transitivity fails unless both partOf relationships have the same CHI type as defined above.

For Example:

piston part of engine
engine part of car
piston part of engine

engine part of car
car part of fleet
engine part of fleet

The Java Collections Framework

The following class diagram shows many of the interfaces and implementation classes in the new Java Collections Framework (located in java.util):

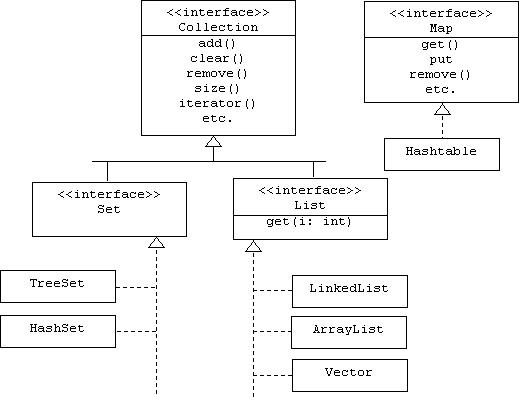
Basically, a set is an unordered collection with no duplicate elements, while a list is an ordered collection with duplicate elements allowed. A map is a table or dictionary. Readers should consult the online Java Tutorial for more details.

Generics and the Standard Template Library

A container is actually a handle that manages a potentially complicated C-style data structure such as an AVL tree, hash table, or doubly linked list (see the Handle-Body idiom discussed in chapter 4). Fortunately, implementing these data structures is largely an academic exercise these days (but a good one). This is because the standard C++ library now comes with a collection of container templates called the Standard Template Library.

Containers can be roughly divided into two types: sets and sequences. Recall from mathematics that a sequence is an ordered set. Thus, the sequence (a, b, c) is different from the sequence (c, b, a), while the set {a, b, c} is the same as the set {c, b, a}. Recall also that multiple occurrences of an element are disregarded in a set, but not a sequence. So the sequence (a, a, b, c) is different from the sequence (a, b, c), while the set {a, a, b, c} is the same as the set {a, b, c}.

Here is a list of the STL containers:

Sequences
vector<Storable> (random access store)
string (derived from vector<char>)
list<Storable> (sequential access store)
deque<Storable> (base class store for stacks and queues)
pair<Key, Storable> (elements of a map)
Sequence Adaptors (temporal access stores)
stack<Storable> (LIFO store)
queue<Storable> (FIFO store)
priority_queue<Storable> (uses Storable::operator<())
Sets
set<Storable>
multiset<Key> (multiple occurences allowed)
map<Key, Storable> (a set of pairs)
multimap<Key, Storable> (a multiset of pairs)

Basic Container Operations

Assume c is an STL container, x is a potential container element, and p is an iterator. Here are some of the most common operations:

c.begin() = iterator "pointing" to first element of c
c.end() = iterator "pointing" to one past last element
c.front() = first element of c
c.back() = last element of c
c.size() = number of elements in c
c.empty() = true if container is empty

c.push_back(x) inserts x at end of c
c.push_front(x) inserts x at beginning of c
c.insert(p, x) inserts x in c before *p

c.pop_front() removes first element of c
c.pop_back() removes last element of c
c.erase(p) removes *p

Vectors

STL vectors encapsulate dynamic arrays (see chapter 4). They automatically grow to accommodate any number of elements. The elements in a vector can be accessed and modified using iterators or indices.

To begin, let's provide a template for printing vectors, this will make a nice addition to our utility library. We use a constant iterator:

template <typename Storable>
ostream& operator<<(ostream& os, const vector<Storable>& v)
{
os << "( ";
vector<Storable>::const_iterator p;
for( p = v.begin(); p != v.end(); p++)
os << *p << ' ';
os << ')';
return os;
}

Here's how we declare an integer vector:

vector<int> vec;

It's easy to add elements to the back of a vector:

vec.push_back(7);
vec.push_back(42);
vec.push_back(19);
vec.push_back(100);
vec.push_back(-13);
cout << vec << endl; // prints (7 42 19 100 –13)

It's also easy to remove elements from the back of a vector:

vec.pop_back(); // removes -13

Of course we can use the subscript operator to access and modify vector elements:

for(int i = 0; i < vec.size(); i++)
vec[i] = 2 * vec[i]; // double each element

The subscript operator is unsafe. It doesn't check for out of range indices. As with strings, we must us the vec.at(i) member function for safe access.

To insert or remove an item from any position in a vector other than the last, we must first obtain an iterator that will point to the insertion or removal position:

vector<int>::iterator p = vec.begin();

Next, we position p:

p = p + 2;

Finally, we insert the item using the insert() member function:

vec.insert(p, 777);
cout << vec << endl; // prints (14 84 77 38 200)

We follow the same procedure to remove an element:

p = vec.begin() + 1;
vec.erase(p);
cout << vec << endl; // prints (14 77 38 200)

Aggregation in UML

UML allows us to model Assembly/Component aggregation using composition or solid-diamond association:

UML also models Container/Member aggregation using (UML) aggregation or hollow-diamond association:

Aggregation (Container/Member Aggregation)

UML also includes a weaker form of composition called aggregation. Conceptually, an aggregation relationship between classes A and B indicate that an instance of A is merely a collection of instances of B. The same instance of B might simultaneously belong to many collections. One of these collections may cease to exist without any effect on its members.

We might have represented the relationship between fleets and airplanes using aggregation, because the same airplane might simultaneously belong to several fleets, and a fleet might disband, but the airplanes that belonged to the fleet still exist. Aggregation is represented in a class diagram by an aggregation "arrow" connecting the aggregate class to its member class:

Although aggregation may have conceptual value (and even this is debatable), it doesn't seem to suggest anything about implementation beyond what is already suggested using an ordinary association.

Implementing Assembly/Component Aggregation

There are several coding conventions that accompany aggregation. For example, an assembly should be responsible for its components. Creating an assembly creates its components, copying an assembly copies its components, and destroying an assembly destroys its components. Copy semantics employed by C++ causes additional concerns, since we can end up with many objects in our program that represent the same object in the domain. This can lead to synchronization and equality problems.

Programming Notes

Equality in Java

It is possible to distinguish between logical equality and literal equality in Java. Two names are literally equal if they are both names of the same object in the computer's memory. We can test for literal equality using the == operator, and literal inequality using the != operator.

For example, let's represent points in the plane using instances of the following class:

class Point {
public double xc = 0; // x coordinate
public double yc = 0; // y coordinate
public String toString() {
return "(" + xc + ", " + yc + ")";
}
// etc.
}

Next, we create several points:

Point p1 = new Point();
Point p2 = new Point();
Point p3 = p1;

Printing the points:

System.out.println("p1 = " + p1);
System.out.println("p2 = " + p2);
System.out.println("p3 = " + p3);

produces the output:

p1 = (0.0, 0.0)
p2 = (0.0, 0.0)
p3 = (0.0, 0.0)

Apparently, all three points are logically equal. In other words, all three represent the origin of the plane. But if we ask if they are literally equal, we get the following results:

p1 == p2 produces false

because new operator was used to create p1 and p2, but

p1 == p3 produces true

because p3 was initialized by p1.

Of course we would also expect:

p1 != p2 produces true
p1 != p3 produces false

Java automatically provides every class with a method called equals(). The default algorithm for this method is a test for literal equality. Therefore:

p1.equals(p2) produces false
p1.equals(p3) produces true

However, we can redefine this method to test for logical equality. For example:

class Point {
public double xc = 0; // x coordinate
public double yc = 0; // y coordinate
public String toString() {
return "(" + xc + ", " + yc + ")";
}
public boolean equals(Point p) {
return (xc == p.xc) && (yc == p.yc);
}
// etc.
}

Now the equals() method tests for logical equality:

p1.equals(p2) produces true
p1.equals(p3) produces true

Reference Semantics in Java

Java provides a variety of assignment operators. The basic assignment simply attaches two names to the same object. Assume we declare two names of Point objects (the Point class was defined earlier):

Point p1, p2;

We attach the name p1 to a new Point object:

p1 = new Point();

and assign p1 to p2:

p2 = p1;

At this point the statements:

System.out.println("p1 = " + p1);
System.out.println("p2 = " + p2);

produce the output:

p1 = (0.0, 0.0)
p2 = (0.0, 0.0)

Next, we alter the x coordinate of p1:

p1.xc = 3.0;

Now the statements:

System.out.println("p1 = " + p1);
System.out.println("p2 = " + p2);

produce the output:

p1 = (0.0, 3.0)
p2 = (0.0, 3.0)

Notice that changes to p1 are also changes to p2!

Cloning in Java

So how do we actually make a copy of an object in Java? Actually, Java automatically provides every class with a copying method named clone(). Unfortunately, this method is protected, hence unavailable to clients. The situation can be remedied by redefining the method as a public method. We can even call the default algorithm, which makes a shallow copy of the object, in our implementation by invoking super.clone(). There are quite a few unpleasant syntactic requirements that must be followed:. These are shown in boldface:

class Point implements Cloneable {
public double xc = 0;
public double yc = 0;
public String toString() {
return "(" + xc + ", " + yc + ")";
}
public boolean equals(Point p) {
return (xc == p.xc) && (yc == p.yc);
}
public Object clone() {
Object obj = null;
try {
obj = super.clone(); // make a shallow copy
} catch (CloneNotSupportedException e) {
System.err.println("Error: " + e);
}
return obj;
}
// etc.
}

We can define p2 as a copy of p1 as follows:

Point p1 = new Point();
Point p2 = (Point)p1.clone();

We alter the x coordinate of p1:

p1.xc = 3.0;

Now the statements:

System.out.println("p1 = " + p1);
System.out.println("p2 = " + p2);

produce the output:

p1 = (0.0, 3.0)
p2 = (0.0, 0.0)

Canonical Form in C++

Generally speaking, a handle-body pair is a pair of objects collaborating to appear to the client as a single object. One object, called the handle, manages the interface with the client, while another object, called the body, provides the application logic.

Here is an idealized outline of a handle-body declaration:

class Body
{ // no client access, handles only!
friend class Handle;
void serviceA();
void serviceB();
// etc.
};

class Handle
{
public:
Handle(Body* b = 0) { myBody = b? b: new Body(); }
void serviceA() { if (myBody) myBody->serviceA(); }
void serviceB() { if (myBody) myBody->serviceB(); }
// etc.
private:
Body* myBody;
};

Note that by default, all Body members are private. Handle objects can access the body members because of the friend declaration. Handles typically delegate client requests to their bodies.

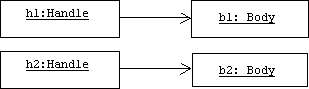
Assume we create two handles:

Handle h1, h2;

The default constructor for Handle, defined above, will automatically create two new bodies for these handles. Let's call them b1 and b2, respectively. The picture in memory looks like this:

Now assume we change our minds and reassign h2 to be like h1:

h2 = h1;

The default assignment algorithm in C++ is called member-wise copy. Each field of h1 is copied to the corresponding field of h2, including the pointer to b1. The new picture looks like this:

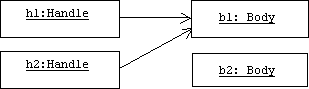
There are two problems with this picture. First, we have a memory leak because b2 was not properly deallocated (remember, the one and only pointer to b2 was encapsulated by h2, so there are no more active references to b2.) Second, we have a potential aliasing problem because h2 and h1 both reference the same body. Changes to the body made through h2 will be reflected in h1.

We summarize these problems, with their standard solution, as the Canonical Form Pattern. Since this pattern is specific to C++, it is more properly designated as an implementation pattern rather than a design pattern:

Canonical Form [COPE], [HORST1]

Other Names

Orthodox Canonical Form, OCF

Problem

Copying a handle does not make a copy of its body, and deleting a handle does not delete its body. This can lead to aliasing problems and memory leaks.

Solution

Provide a copy constructor and assignment operator that make copies of the body; also provide a destructor that deletes the body.

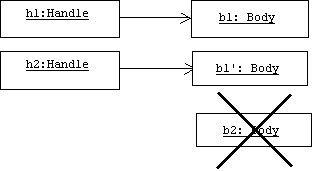
The new assignment operator does nothing if its right- and left-hand sides are the same. Otherwise, the old body is deleted by calling a private supporting function, free(), and a copy of the body belonging to the handle on the right-hand side of the assignment operator is created. The address of this new body is assigned to the myBody variable of the handle on the left-hand side of the assignment operator. All of this is accomplished by a private supporting function called copy():

Handle& Handle::operator=(const Handle& h)
{
if (&h != this) // x = x is a no-op
{
free(); // delete myBody
copy(h); // point myBody to a copy of *(h.myBody)
}
return *this;
}

After the h2 = h1 assignment the picture will now look like this:

Handles can also be copied by copy constructors, again the default algorithm is member-wise copy, hence we must redefine the copy constructor to call the private copy() function described above:

Handle::Handle(const Handle& h)
{
copy(h); // point myBody to a copy of *(h.myBody)
}

Whenever we define a constructor, we must also define a default constructor, otherwise we will loose the default constructor provided by C++. The default constructor is important because it is always used to initialize arrays of class instances. Also, derived class constructors automatically call their base class' default constructor (unless a different constructor is specified in the initializer list).

Handle::Handle(Body* b /* = 0 */)
{
myBody = (b? b: new Body());
// initialize any other fields
}

We must also provide a destructor that automatically deallocates the body when the handle is deallocated. Our destructor calls free(), the private supporting function mentioned earlier:

Handle::~Handle()
{
free(); // delete myBody
}

The copy() and free() functions are private member functions that encapsulate the details of copying and deleting bodies. If the body is a properly defined C++ object, then a simple implementation might be:

void Handle::free() { if (myBody) delete myBody; }

void Handle::copy(const Handle& h)
{
myBody = new Body(*(h.myBody));
// copy any other fields of h
}

But in most cases the implementations will depend on the details of the body. The new declaration of the Handle class looks like this:

class Handle
{
public:
Handle(Body* b = 0);
Handle(const Handle& h) { copy(h); }
~Handle() { free(); }
Handle& operator=(const Handle& h);
void serviceA() { if (myBody) myBody->serviceA(); }
void serviceB() { if (myBody) myBody->serviceB(); }
// etc.
private:
Body *myBody;
void free();
void copy(const Handle& h);
};

The members shown in bold face are required by the Canonical Form pattern for every handle class.

Equality in C++

C++ allows programmers to overload many operators, including the == operator. For example, the expression:

a == b

is equivalent to the function call:

operator==(a, b)

Since C++ allows overloading, a programmer may provide his own definition for this function:

boolean operator==(const Handle& h1, const Handle& h2) {
// determine if h1 and h2 are logically equivalent
}

Implementing Container/Member Aggregation

Using STL in C++

How will our magic CASE tool represent the association between Fleet and Airplane? Of course the association is unidirectional, so we won't need to make any changes to our Airplane class. But instances of our Fleet class need to hold zero or more Airplane pointers. Placing a static array of Airplane pointers in the Fleet class will impose a maximum size on fleets and will be difficult to manage. Instead, a linked list, dynamic array, or set should be used. Several libraries include implementations of these data structures, including the standard C++ library, which provides vector<T>, list<T>, set<T>, and multiset<T> container templates as well as iterators for accessing their stored elements:[1]

class Fleet
{
public:
typedef set<Airplane*>::iterator iterator;
void add(Airplane* a) { members.insert(a); }
void rem(Airplane* a) { members.erase(a); }
iterator begin() { return members.begin(); }
iterator end() { return members.end(); }
private:
set<Airplane*> members;
};

Alternatively, we can make Fleet a subclass that privately inherits the features of its set<Airplane*> super-class:

class Fleet: set<Airplane*>
{
public:
void add(Airplane* a) { insert(a); }
void rem(Airplane* a) { erase(a); }
iterator begin() { return set<Airplane*>::begin(); }
iterator end() { return set<Airplane*>::end(); }
};

The need for private inheritance becomes clear if we want to place restrictions on the type of airplanes that can be added to a fleet. For example, assume all airplanes must pass a quality test before they can be added to a fleet:

class Fleet: set<Airplane*>
{
public:
void add(Airplane* a) { if (test(a)) insert(a); }
// etc.
private:
bool test(Airplane* a);
};

Private inheritance prevents low quality planes from being added to the fleet through the "back door". For example, assume a particular plane doesn't pass the quality test for a particular fleet:

Fleet panAm;
Airplane junkHeap;
panAm.add(&junkHeap); // this fails

Thanks to private inheritance, Fleet clients can't call member functions inherited from the set<Airplane*> base class:

panAm.insert(&junkHeap); // this fails, too!

Using JCF in Java

We could provide a Java Fleet with a set of Airplane references:

class Fleet {
private Set members = new HashSet();
public void add(Airplane a) { members.add(a); }
public void rem(Airplane a) { members.remove(a); }
public Iterator iterator() { return members.iterator(); }
}

A Java iterator is initialized so that it points to a "location" before the first element of its implicit argument, and provides methods for determining if there is a next element and for moving to and accessing the next element. For example, assume a fleet of three airplanes is created:

Fleet united = new Fleet();
united.add(new Airplane());
united.add(new Airplane());
united.add(new Airplane());

Here is how we would command each airplane in the fleet to takeoff:

Iterator it = united.iterator();
while(it.hasNext()) {
Airplane a = (Airplane)it.next();
a.takeoff();
}

The explicit downcast is necessary because Java collections hold Objects. Since every class implicitly extends the Java Object class, templates aren't needed.

The Composite Design Pattern

A calculator is an example of a composite object. We can treat it as an individual object that encapsulates its components: the menu bar, toolbar, buttons, labels, and boxes, or, when it's convenient, we can ignore the calculator and treat its components as individual objects.

Of course some of the calculator's components are also composites. For example, the toolbar is a composite consisting of several buttons. Sometimes it's convenient to think of a calculator as a tree-like structure:

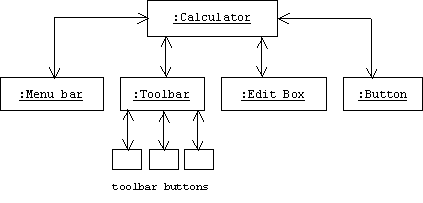
Composites are so common, that they are included in many pattern catalogs:

Composite [Go4], [POSA]

Other Names

Composites are also called assemblies, wholes, aggregates, and trees. Components are also called parts.

Problem

Sometimes a composite structure must be viewed as a single object that encapsulates its components. Other times we need to change or analyze the individual components, which may also be composite structures.

Solution

If we call components without parts atoms, then we can view Atom and Composite as specializations of an abstract Component class. We define aggregation as the relationship between Composite and Component.

Static Structure

In some formulations each component maintains a reference to its parent:

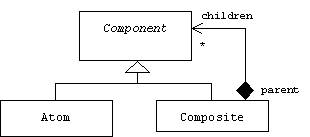
We have already seen many instances of the composite pattern. For example, files are atoms and directories are composites, the leaf nodes of a tree are atoms, while the composites are parent nodes. In Microsoft's terminology components are called "windows" and atoms are called "controls".

Reference

James Odell; Six Different Kinds of Composition; Journal of Object-Oriented Programming Vol 5, No 8. January 1994.

---

[1] The standard library container templates are discussed in Appendix 1.