4. Polymorphism and Data-Driven Control
Overriding versus Overloading
Java, like many modern languages, allows different methods to share the same name as long as their parameter lists are different. This is called overloading. For example, the following calculator class contains four variants of the overload method:
class Calculator {
int result;
void add(int x) { result += x; }
void add(long x) { result += x; }
void add(float x) { result += x; }
void add(int x, int y) { result += x %
y; }
// etc.
}
The virtual machine performs variant selection by analyzing the number and types of arguments passed to the method:
Calculator calc = new Calculator();
calc.add(42); // call int variant
calc.add(42L); // call long variant
calc.add(42F); // call float variant
calc.add('X'); // call int variant
Overriding
A subclass inherits the fields and methods of its superclass. The subclass may declare new methods. Some of these methods may overload inherited methods. For example, assume a simple floating point calculator has been declared:
class Calculator {
double result;
void add(double arg) { result += arg; }
// etc.
}
We would like to add a mode that allows us to do integer arithmetic. We can accomplish this in an extension:
class IntCalculator extends Calculator {
int result;
boolean intMode = true;
void add(int arg) {
if (intMode) result += arg;
else super.add(arg);
}
// etc.
}
Study the result of executing the following test code:
IntCalculator calc = new IntCalculator();
calc.add(42F); // calc.super.result = 42.0
calc.add(42); // calc.result = 42
calc.intMode = false;
calc.add(42); // calc.super.result = 84.0
There are several points to notice. First, calc has two variants of the add method. The inherited double variant, and the declared integer variant. The compiler chose to call the inherited variant in the line:
calc.add(42F);
and chose to call the integer variants in the third and fifth lines.
Second, notice that the integer variant calls the inherited variant if the intMode flag is false. This is done by qualifying the call using super:
super.add(arg);
Alternatively, since the inherited result field has package scope, the integer variant could have executed:
super.result += arg;
Let's make a minor change to IntCalculator. We simply change the parameter of add from int to double:
class IntCalculator extends Calculator {
int result;
boolean intMode = true;
void add(double arg) {
if (intMode) result += arg;
else super.add(arg);
}
// etc.
}
Study the following test harness:
IntCalculator calc = new IntCalculator();
calc.add(42F); // calc.result = 42
calc.add(42); // calc.result = 84
calc.add(3.14); // calc.result = 87
Clearly, IntCalculator.add() was called all three times. This happens because the new add method has the same signature as the inherited add method and therefore overrides or redclares it rather than overloads it.
A method in a subclass overrides an inherited method provided:
1. it has the same signature (name, parameters, and return type)
2. it has the same extent (static or heap)
3. throws a subset of the exceptions thrown by the inhertited method.
Final Fields and Methods in Java
Java programmers can prevent overriding (but not overloading) by declaring a method to be final:
class Calculator {
int result;
final void add(int x) { result += x; }
final void add(long x) { result += x; }
final void add(float x) { result += x;
}
final void add(int x, int y) { result
+= x % y; }
// etc.
}
Declaring a field to be final has the effect of making it a constant:
class Fleet {
private static final int MAX = 100;
private Aircraft[] members = new
Aircraft[MAX];
private int size = 0;
// etc.
}
Polymorphism and Dynamic Dispatch
Assume a fleet contains many types of aircraft.
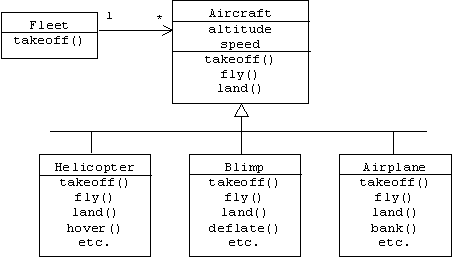
Although Aircraft defines default takeoff, fly, and land methods, these methods are overridden in the subclasses by more appropriate algorithms:
class Aircraft {
public void takeoff() {
System.out.println("An aircraft
is taking off");
}
// etc.
}
class Blimp extends Aircraft {
public void takeoff() {
System.out.println("A blimp is
taking off");
}
// etc.
}
The Fleet.takeoff() method iterates through the fleet members, calling the takeoff() method of each one:
class Fleet {
private static final int MAX = 100;
private Aircraft[] members = new
Aircraft[MAX];
private int size = 0;
public void add(Aircraft a) {
if (size < MAX) members[size++] =
a;
}
public void takeoff() {
for(int i = 0; i < size; i++)
members[i].takeoff();
}
}
One would assume that the command:
members[i].takeoff()
would call the generic Aircraft.takeoff() method. This isn't the case, however. If members[i] is a reference to a Blimp, then Blimp.takeoff() is called. If members[i] is a reference to a Helicopter, then Helicopter.takeoff() is called, etc. This is possible because of polymorphism and dynamic dispatch. The Polymorphism Principle (also called the Subsumption Rule), states:
If v is an object of type B, and if B is a subclass of A, then v is also of type A.
In other words:
If B is a subclass of A, then an object of type B can be used in any context where an object of type A is expected.
We see the Polymorphism Principle at work in our statement:
members[i].takeoff()
Obviously, we expected members[i] to be an object of type Aircraft, however, members[i] can refer to objects of type Airplane, Blimp, and Helicopter. Neither the Java compiler nor the Java Virtual Machine will complain. We would have also seen this in calls to the Fleet.add method:
Fleet united = new Fleet();
united.add(new Blimp());
united.add(new Airplane());
united.add(new Helicopter());
// etc.
The Fleet.add() method expects an aircraft argument, but in each case was called with an argument that belonged to a subtype of Aircraft.
The Dynamic Dispatch Mechanism complements the Polymorphism Principle:
When an object receives a message, the object decides which message handler should be invoked.
This idea doesn't sound too radical, but remember, objects only exist at runtime. This means at compile time, implementation time, even at design time, we have no clear idea what method will be invoked. We can stare at the line:
members[i].takeoff()
as much as we want, but no one can say for sure which code will actually run when this line is executed. This idea is a little unsettling for programmers who are used to dictating the flow of control through their programs. It is also a little unsettling for compilers and linkers that want to resolve all bindings before execution begins.
Normally, dynamic dispatch is implemented by equipping each object with a dispatch table that matches message types with message handlers:

When an object receives a message like "takeoff", it searches its dispatch table for the appropriate message handler to invoke. (This search adds a little bit of extra time to the program execution, and of course the dispatch tables consume a little more memory.) Although two objects may receive the same "takeoff" message, they may have different dispatch tables, hence may invoke different message handlers. For example, blimps will invoke Blimp.takeoff(), while airplanes invoke Airplane.takeoff().
Polymorphism in C++
Dynamic dispatch is not the default in C++. The compiler pairs messages with handlers based on available type information. Only handlers explicitly labeled "virtual" are invoked dynamically in the way described above:
class Aircraft
{
public:
virtual void takeoff();
virtual void fly();
virtual void land();
}
Data-Driven Programming
Combining Polymorphism with Dynamic Dispatch opens the door to an entirely new style of programming called Data-Driven Programming. In Data-Driven Programming, sequence control is determined by the data, not the programmer. We saw this in our famous line of code:
members[i].takeoff()
The poor programmer has no idea what method will be called. This decision is made by the object referenced by members[i].
Data-Driven Programming contrasts with the more traditional Control-Driven Programming, in which the programmer explicitly determines the flow of control. here's a control-driven version of Fleet.takeoff():
class Fleet {
private static final int MAX = 100;
private Aircraft[] members = new
Aircraft[MAX];
private int size = 0;
public void takeoff() {
for(int i = 0; i < size; i++) {
if (members[i] instanceof Blimp)
((Blimp)members[i]).takeoff();
else if (members[i] instanceof
Airplane)
((Airplane)members[i]).takeoff();
else if (members[i] instanceof
Helicopter)
((Helicopter)members[i]).takeoff();
else
System.err.println("unrecognized
aircraft");
}
}
// etc.
}
The problem with this approach occurs when a new type of aircraft is introduced into our Aircraft hierarchy:
class Saucer extends Aircraft {
void takeoff() {
System.out.prinntln("A flying
saucer is taking off");
}
// etc.
}
The control-driven programmer must now add a line to Fleet.takeoff():
else if (members[i] instanceof Saucer)
((Saucer)members[i]).takeoff();
There are two problems with this. First, Fleet is a client of the Aircraft hierarchy. Our design requires a modification of the client code each time the Aircraft hierarchy is extended. What if the client code wasn't available, or what if it is mission-critical code found in an air traffic control tower. Second, how many places in the client code must be modified? How many places did the client assume there were only three types of aircraft? This multi-way conditional could occur hundreds of times in the client code. If we forget to modify just one of these occurrences, then we will have introduced a bug into the client's code!
Control-Driven Programming in C++
C++ doesn't provide an instanceof operator. Instead, the programmer must provide an equivalent mechanism:
class Aircraft {
int type;
public:
enum {UNKNOWN, AIRPLANE, HELICOPTER,
BLIMP};
int getType() { return type; }
Aircraft(int tp = UNKNOWN) {
type = tp;
}
// etc.
};
class Fleet {
enum {MAX = 100;};
Aircraft members[] = new Aircraft[MAX];
int size ;
public:
void takeoff() {
for(int i = 0; i < size; i++) {
if (members[i].getType() ==
Aircraft::Blimp)
((Blimp)members[i]).takeoff();
else if (members[i].getType() ==
Aircraft::Airplane)
((Airplane)members[i]).takeoff();
else if (members[i].getType() ==
Aircraft::Helicopter)
((Helicopter)members[i]).takeoff();
else
cerr << "unrecognized
aircraft";
}
}
// etc.
}
Abstract Classes
Returning to the Data-Driven implementation of Fleet.takeoff(), what happens when we call
members[i].takeoff()
and members[i] refers to a flying saucer, and yet the implementer of the Saucer class forgot to provide a takeoff() method? No problem, the Saucer class inherited the default takeoff() method from the Airplane class. So in this case Aircraft.takeoff() will be called.
But is this desirable? Our Aircraft.takeoff() method simply prints a message. In a real-world application calling this method could be a disaster. We can remedy this situation by not providing a default takeoff method in the Aircraft class. But now the compiler won't compile
members[i].takeoff()
The problem is that there's no guarantee that every aircraft will have a takeoff() method.
The correct remedy is to provide the Aircraft class with an abstract takeoff() method. Abstract methods have no bodies:
abstract class Aircraft {
public abstract void takeoff();
// etc.
}
Of course we can no longer instantiate the Aircraft class:
Aircraft a = new Aircraft(); // ERROR!
a.takeoff(); // because what happens here?
Now the compiler requires subclasses to implement a takeoff() method. If the implementer of Saucer forgets to provide a takeoff() method, then Saucer also becomes an abstract class, and attempting to instantiate the saucer class is a compile-time error:
united.add(new Saucer()); // COMPILER ERROR!
Abstract Classes in C++
class Aircraft
{
public:
Aircraft(double a = 0.0, double s =
0.0)
{
altitude = a;
speed = s;
}
virtual ~Aircraft() {}
double getSpeed() const { return speed;
}
double getAltitude() const { return
altitude; }
void setSpeed(double s) { speed = s; }
void setAltitude(double a) { altitude =
a; }
// these functions must be defined by
derived classes:
virtual void takeoff() = 0;
virtual void fly() = 0;
virtual void land() = 0;
protected:
double altitude, speed;
};
Abstract Classes in UML
Names of abstract classes and virtual functions are italicized in UML:
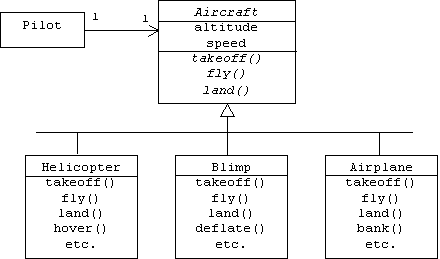
Interfaces
When it is time to upgrade or replace a chip in a computer, the old chip is simply popped out of the motherboard, and the new chip is plugged in. It doesn't matter if the new chip and old chip have the same manufacturer or the same internal circuitry, as long as they both "look" the same to the motherboard and the other chips in the computer. The same is true for car, television, and sewing machine components. Open architecture systems and "Pluggable" components allow customers to shop around for cheap, third-party generic components, or expensive, third-party high-performance components.
An interface is a collection of operator specifications. An operator specification may include a name, return type, parameter list, exception list, pre-conditions, and post-conditions. A class implements an interface if it implements the specified operators. A software component is an object that is known to its clients only through the interfaces it implements. Often, the client of a component is called a container. If software components are analogous to pluggable computer chips, then containers are analogous to the motherboards that contain and connect these chips. For example, an electronic commerce server might be designed as a container that contains and connects pluggable inventory, billing, and shipping components. A control panel might be implemented as a container that contains and connects pluggable calculator, calendar, and address book components. Java Beans and ActiveX controls are familiar examples of software components.
Interfaces and Components in UML
Modelers can represent interfaces in UML class diagrams using class icons stereotyped as interfaces. The relationship between an interface and a class that realizes or implements it is indicated by a dashed generalization arrow:
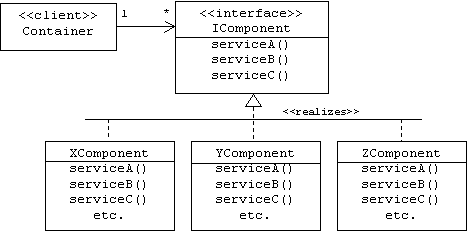
Notice that the container doesn't know the type of components it uses. It only knows that its components realize or implement the IComponent interface.
For example, imagine that a pilot flies an aircraft by remote control from inside of a windowless hangar. The pilot holds a controller with three controls labeled: TAKEOFF, FLY, and LAND, but he has no idea what type of aircraft the controller controls. It could be an airplane, a blimp, a helicopter, perhaps it's a space ship. Although this scenario may sound implausible, the pilot's situation is analogous to the situation any container faces: it controls components blindly through interfaces, without knowing the types of the components. Here is the corresponding class diagram:
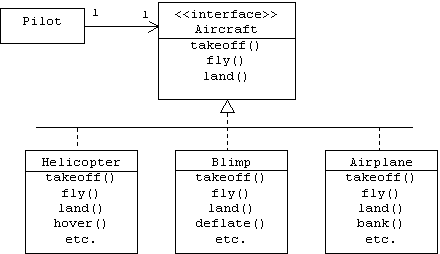
Notice that all three realizations of the Aircraft interface support additional operations: airplanes can bank, helicopters can hover, and blimps can deflate. However, the pilot doesn't get to call these functions. The pilot only knows about the operations that are specifically declared in the Aircraft interface.
We can create new interfaces from existing interfaces using generalization. For example, the Airliner interface specializes the Aircraft and (Passenger) Carrier interfaces. The PassengerPlane class implements the Airliner interface, which means that it must implement the operations specified in the Aircraft and Carrier interfaces as well. Fortunately, it inherits implementations of the Aircraft interface from its Airplane super-class:
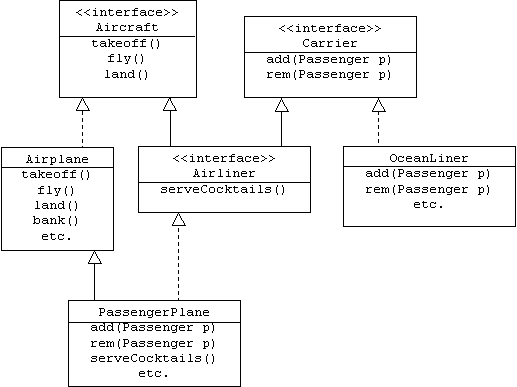
An interface is closely related to the idea of an abstract data type (ADT). In addition to the operator prototypes, an ADT might also specify the pre- and post-conditions of these operators. For example, the pre-condition for the Aircraft interface's takeoff() operator might be that the aircraft's altitude and airspeed are zero, and the post-condition might be that the aircraft's altitude and airspeed are greater than zero.
Interfaces and Components in Java
Java allows programmers to explicitly declare interfaces:
interface Aircraft {
public void takeoff();
public void fly();
public void land();
}
Notice that the interface declaration lacks private and protected members. There are no attributes, and no implementation information is provided.
A Pilot uses an Aircraft reference to control various types of aircraft:
class Pilot {
private Aircraft myAircraft;
public void fly() {
myAircraft.takeoff();
myAircraft.fly();
myAircraft.land();
}
public void setAircraft(Aircraft a) {
myAircraft = a;
}
// etc.
}
Java also allows programmers to explicitly declare that a class implements an interface:
class Airplane implements Aircraft {
public void takeoff() { /* Airplane
takeoff algorithm */ }
public void fly() { /* Airplane fly
algorithm */ }
public void land() { /* Airplane land
algorithm */ }
public void bank(int degrees) { /* only
airplanes can do this */ }
// etc.
}
The following code shows how a pilot flies a blimp and a helicopter:
Pilot p = new Pilot("Charlie");
p.setAircraft(new Blimp());
p.fly(); // Charlie flies a blimp!
p.setAircraft(new Helicopter());
p.fly(); // now Charlie flies a helicopter!
It is important to realize that Aircraft is an interface, not a class. As such, it cannot be instantiated:
p.setAircraft(new Aircraft()); // error!
Java also allows programmers to create new interfaces from existing interfaces by extension:
interface Airliner extends Aircraft, Carrier {
public void serveCocktails();
}
Although a Java class can only extend at most one class (multiple inheritance is forbidden in Java), a Java interface can extend multiple interfaces and a Java class can implement multiple interfaces. A Java class can even extend and implement at the same time:
class PassengerPlane extends Airplane implements Airliner {
public void add(Passenger p) { ... }
public void rem(Passenger p) { ... }
public void serveCocktails() { ... }
// etc.
}
Interfaces and Components in C++
C++ is much older than Java, so it doesn't allow programmers to explicitly declare interfaces. Instead, we'll have to fake it using classes that only contain public, pure virtual functions:
class Aircraft // interface
{
public:
virtual void takeoff() = 0;
virtual void fly() = 0;
virtual void land() = 0;
};
A client references a component through an interface typed pointer:
class Pilot
{
public:
void fly()
{
myAircraft->takeoff();
myAircraft->fly();
myAircraft->land();
}
void setAircraft(Aircraft* a) { myAircraft
= a; }
// etc.
private:
Aircraft* myAircraft;
};
Instead of explicitly declaring that a class implements an interface as one does in Java, C++ programmers must declare that a class is derived from an interface. Because all of the interface member functions are pure virtual, this will require the derived class to provide implementations:
class Airplane: public Aircraft
{
public:
void takeoff() { /* Airplane takeoff
algorithm */ }
void fly() { /* Airplane fly algorithm
*/ }
void land() { /* Airplane land
algorithm */ }
void bank(int degrees) { /* only
airplanes can do this */ }
// etc.
};
In the following code snippet a pilot first flies a blimp, then a helicopter. Unlike Java, the question of deleting the blimp remains open:
Pilot p("Charlie");
p.setAircraft(new Blimp());
p.fly(); // Charlie flies a blimp!
p.setAircraft(new Helicopter());
p.fly(); // now Charlie flies a helicopter!
Interfaces and be constructed from existing interfaces through the C++ derived class mechanism, too:
class Airliner: public Aircraft, public Carrier
{
public:
virtual void serveCocktails() = 0;
};
Here is a C++ implementation of the Airliner interface:
class PassengerPlane: public Airplane, public Airliner
{
public:
void add(Passenger p) { ... }
void rem(Passenger p) { ... }
void serveCocktails() { ... }
};
Notes
Type Systems
A type consists of a domain of values plus a set of operations[1]:
type = <domain, operations>
In a typed language expressions and values have types. Expressions produce values when they are evaluated. We expect the type of an expression to be equivalent to the type of value it produces when evaluated.
A type system is a set of primitive types together with a set of rules for introducing new types and for determining if the following assertions are valid:
v is a value or expression of type T (v: T)
type T1 is equivalent to type T2 (T1 ~ T2)
type T1 is a subtype of type T2 (T1 <: T2)
For example, a types system S might contain the primitive types:
int, boolean, and error
as well as the following type introduction rules:
If T1 and T2 are types, then so are:
T1 -> T2 = { f | domain(f) = T1
&& range(f) = T2 }
T1 x T2 = { (a, b) | a: T1 &&
b: T2 }
T[] = { a | a[i]: T }
Type Equivalence
Of course type equivalence satisfies the rules of any equivalence relationship:
T ~ T
T1 ~ T2 implies T2 ~ T1
T1 ~ T2 and T2 ~ T3 implies T1 ~ T3
Type systems can use name or structural equivalence. Structural equivalence in S means two types are equivalent if they have the same structure:
Assume T1 ~ T2 &&
T3 ~ T4, then
T1 x T3 ~ T2 x T4
T2 -> T4 ~ T1 -> T3
T1[] ~ T2[]
Many type systems allow programmers to name new types in type declarations:
type Point = int x int
type Vector = int x int
type Metric = Vector->int
type Polygon = Point[]
Name equivalence says two types are equivalent if an only if they have the same name. Thus, even though Point and Vector are structurally equivalent, they are not name equivalent.
Subtypes, Inheritance, and Subsumption
Some type systems provide rules for determining if one type is a subtype of another. Intuitively, if T1 is a subtype of T2 (equivalently: T2 is a supertype of T1):
T1 <: T2
if the domain of T1 is constrained by the domain of T2:
dom(T1) = S3 x S2 x S4 where S3 and S4 are arbitrary domains and S2 is a subdomain of dom(T2)
Often the notion of subtype is coupled with the idea of inheritance. If T1 is a subtype of T2, then T1 inherits from T2 if the operations of T2 are a subset of the operations of T1:
ops(T1) is a subset of ops(T2)
The subtype relationship satisfies the rules for a partial ordering:
T1 ~ T2, then T1 <: T2
T1 <: T2 and T2 <: T3, then T1 <: T3
Our type system S also satisfy the rules:
boolean <: int
Assume T1 <: T2
&& T3 <: T4, then
T1 x T3 <: T2 x T4
T2 -> T4 <: T1 -> T3
T1[] <: T2[]
error <: T for all T
A polymorphic type system allows values of type T1 to be used in contexts where values of type T2 are expected. This is called the Subsumption Rule:
v: T1 and T1 <: T2, then v: T2
The Java Type System
Java types are either primitive, reference, or method types.
The primitive types of Java are:
boolean = {false, true}
char = { '\uXXXX' | 0 <= X <= F }
byte = { n | -2k <= n < 2k for k = 8 }
short = { n | -2k <= n < 2k for k = 16 }
int = { n | -2k <= n < 2k for k = 32 }
long = { n | -2k <= n < 2k for k = 64 }
float = { n * 2m | -2-k <= n < 2k, k =
23 && -2-k <= m < 2k, k = 8 }
double = { n * 2m | -2-k <= n < 2k, k =
52 && -2-k <= m < 2k, k = 11 }
The reference types of Java are array types, interface types, and class types.
We regard the signature of a method as the type of that method.
Example: Recall the declaration of Polygon class:
class Polygon {
private Point[] vertices;
private int numVerts = 0;
public void add(Point p) {...}
public void remove(Point p) {...}
public Point get(int i) {...}
}
The type of the get method is its signature:
Point Polygon.get(int)
The vertices field is an array type:
Point[]
Polygon is both a class and a class type. Most type systems would insist that the Polygon type is the Polygon class without its private members, constructors, or method implementations. We can capture this idea with a Java interface declaration:
interface PolygonType {
void add(Point p);
void remove(Point p);
Point get(int i);
}
In addition, we must explicitly declare that the Polygon class implements the PolygonType:
class Polygon implements PolygonType { ... }
Subtypes and Subsumption
In Java, the compatibility relationship, T1 <: T2, means T1 is a subtype of T2. Of course it is a partial ordering:
T <: T
T1 <: T2 && T2 <: T3, then T1 <: T3
Here are the relationships between the primitive types, notice that boolean is incompatible with everything:
byte <: short <: int <: long <: float <: double
char <: int
For the reference types:
T1 extends T2 implies T1 <: T2
T1 implements T2 implies T1 <: T2
T1 <: T2 implies T1[] <: T2[]
Finally, if T1 is a primitive type and T2 is a reference type, then T1 <: T2 is never true, and T2 <: Object is always true.
A type system is polymorphic if it satisfies the subsumption rule:
val: T1 && T1 <: T2 implies val: T2
In other words, T1 a subtype of T2 implies a value of type T1 can be used in any context where a value of type T2 is expected.
Example
Of course we can use integers and floats in contexts where doubles are expected:
Math.cos(0);
Math.cos(0L);
Math.cos(.0F);
Math.cos(.0);
Example
Assume the following classes have been declared:
class Aircraft {
void takeoff() { ... }
void fly() { ... }
void land() { ... }
}
class Airplane extends Aircraft { ... }
class Jet extends Airplane { ... }
class Blimp extends Aircraft { ... }
class Helicopter extends Aircraft { ... }
We have the following subclass relationships:
Jet <: Airplane <: Aircraft
Helicopter <: Aircraft
Blimp <: Aircraft
In other words, jets, airplanes, blimps, and helicopters can be used in contexts where aircraft are expected. For example, an array of aircraft can hold jets, airplanes, blimps, and helicopters:
Aircraft[] fleet = new Aircraft[4];
fleet[0] = new Airplane();
fleet[1] = new Helicopter();
fleet[2] = new Blimp();
fleet[3] = new Jet();
Such an array is called a heterogeneous container, because it contains different types of objects. Traversing a heterogeneous array is just like traversing a homogeneous array, because we know each object in the array inherits the methods of its super class:
for(int i = 0; i < 4; i++) {
fleet[i].takeoff();
fleet[i].fly();
fleet[i].land();
}
As another example, the following method has an aircraft parameter:
class Pilot {
void fly(Aircraft a) {
a.takeoff();
a.fly();
a.land();
}
// etc.
}
But we can pass airplane, jet, helicopter, and blimp arguments to this method:
Pilot p = new Pilot();
p.fly(new Airplane());
p.fly(new Jet());
p.fly(new Helicopter());
p.fly(new Blimp());
Type Conversion
The subsumption rule guarantees that a value of type T1 can be used in a context where a value of type T2 is expected if T1 is a subtype of T2. To keep this promise, the value may need to be retyped or coerced. For example, using a reference to a jet in a context where a reference to an aircraft is expected only involves temporarily retyping the reference to the jet as a reference to an aircraft. However, using an integer in a context where a double is expected requires that the integer be transformed or coerced into an equivalent double precision number. In either case, these conversions are implicit or automatic.
The programmer may explicitly request a conversion by using the casting operator:
(T)val;
For example:
Aircraft a = new Jet(); // implicit retyping (widening
conversion)
Jet j = (Jet)a; // explicit retyping (narrowing conversion)
int n = (int) Math.PI; // explicit coercion (narrowing conversion)
Generally speaking, explicit casts allow us to move from supertypes to subtypes:
T1 <: T2 && v: T2 implies (T1)v: T1
Invariance, Covariance, and Contravariance
Recall that our hypothetical type system, S, satisfied the rule:
If T1 <: T2 && T3 <: T4, then T2 -> T4 <: T1 -> T3
In other words, if f is a map (function, method) with domain T2 and range T4, then f can also be regarded as a map with domain T1 and range T3, where T4 is a subtype of T3 and T1 is a subtype of T2. We say that a map type T1 -> T2 is covariant in its range, and contravariant in its domain.
If we equate method signatures with map types, then the Java type system does not satisfy this rule. For example, in the following declarations:
class T2 { }
class T1 extends T2 { }
class T4 { }
class T3 extends T4 { }
public class TypeDemo {
public T1 meth(T4 x) { return new T1();
}
public T2 meth(T3 x) { return new T2();
}
// etc.
}
Java regards the two methods of TypeDemo as distinct overloads of the name meth.
The notion of covariance and contravariance can be generalized to the pre- and post-conditions of a method. For example, assume a Java class called SubClass extends a class called SuperClass, and overrides a method called m:
class SuperClass {
T m(S x) { ... }
...
}
class SubClass extends SuperClass {
T m(S x) { ... }
...
}
Assume
PRE(SubClass.m) = the pre-condition of SubClass.m
POST(SubClass.m) = the post-condition of SubClass.m
PRE(SuperClass.m) = the pre-condition of SuperClass.m
POST(SuperClass.m) = the post-condition of SuperClass.m
We can get into trouble with the Subsumption rule (which Java's type system does satisfy), if we do not follow the following rules:
Covariance Rule
POST(SubClass.m) implies POST(SuperClass.m)
Contravariance Rule
PRE(SuperClass.m) implies PRE(SubClass.m)
To understand this, imagine SuperClass.m is a filter in a pipeline. Imagine the diameter of a pipe corresponds to the range of values that can pass through the pipe. Assume the inputs and outputs of SuperClass.m have sizes that match their input and output pipes, respectively:

To transparently swap SubClass.m for SuperClass.m, as the rule of subsumption demands, then the input of SubClass.m must be at leas as large as the input of SuperClass.m, and the output of SubClass.m must be no larger than the output of SuperClass.m:

Example
Employee bonuses are computed relative to their performance scores.
The type of Employee.calcBonus() is its signature:
double Employee.calcBonus(int performance)
The pre-condition is:
10 <= performance
The post condition is:
bonus <= 1000
We can use assert statements[2] to enforce these conditions:
class Employee {
double salary;
double calcBonus(int performance) {
assert 10 <= performance;
double bonus = 1000;
assert bonus <= 1000;
}
// etc.
}
Programmer bonuses are computed using a slightly different algorithm. The type of Programmer.calcBonus is the same as Employee.calcBonus():
double Programmer.calcBonus(int performance)
The pre condition is:
5 <= performance
The post condition is:
bonus <= 500
We can use assert statements to enforce these conditions:
class Programmer extends Employee {
double calcBonus(int performance) {
assert 5 <= performance;
double bonus = 500;
assert bonus <= 500;
}
// etc.
}
Notice that the pre-condition for Programmer.calcBonus is weaker than the pre-condition for Employee.calcBonus:
10 <= performance implies 5 <= performance
Also notice that the post-condition for Programmer.calcBonus is stronger than the post-condition for Employee.calcBonus:
bonus <= 500 implies bonus <= 1000
A client passes 10 to each employee calcBonus method, and expects a return values less than or equal to 1000.
class Company {
Employee[] staff;
int staffSize = 0;
public void giveBonuses() {
for(int i = 0; i < staffSize;
i++) {
double bonus =
staff[i].calcBonus(10);
if (bonus <= 1000) {
staff[i].salary += bonus;
} else {
System.err.println("error,
no bonus given");
}
}
// etc.
}
Clearly, this code works even when staff[i] contains a reference to a programmer.
Invariance Rule (Closed Behavior)
Subtyping and subsumption gets more confusing when blended with the concept of state space and class invariant.
Let INV(A) represent the invariant condition for class A. Assume SubClass extends SuperClass, then the Subtype Invariance Rule is:
INV(SubClass) implies INV(SuperClass)
For example, assume the following Java declarations have been made:
class Quadrilateral {
// lenghts of my four sides:
double left, right, top, bottom;
// etc.
}
class Rectangle extends Quadrilateral {
// etc.
}
class Square extends Rectangle {
// etc.
}
The invariant of Rectangle is:
INV(Rectangle) = (left == right && top == bottom)
The invariant of Square is:
INV(Square) = (left == right == top == bottom)
Clearly:
INV(Square) implies INV(Rectangle)
A mutator method changes the state of its object. If a subclass overrides a mutator, then the Subclass Invariance Rule implies the overriding mutator must not place its object in a state that satisfies the superclass' invariant, but not the subclass invariant. On the other hand, the Subsumption Rule says subclass instances can be used in contexts where instances of the superclass are expected; including contexts where a superclass instance is being put in a state that satisfies the superclass invariant, but not the subclass invariant.
To resolve this contradiction, we must obey the Mutator Invariance Rule:
PRE(SubClass.mutator) if and only if PRE(SuperClass.mutator)
POST(SubClass.mutator) if and only if POST(SuperClass.mutator)
Example
The state space of the Employee class is the set of all salaries. The class invariant is that a salary must be less than or equal to $100000.
class Employee {
double salary = 0; // <= $100000
void setSalary(double amt) {
assert salary <= 100000;
salary = amt;
assert salary <= 100000;
}
// etc.
}
Assume the Programmer subclass overrides this method with one that has a stronger class invariant:
class Programmer extends Employee {
void setSalary(double amt) {
assert salary <= 90000;
salary = amt;
assert salary <= 90000;
}
// etc.
}
Assume staff is an array of Employee references:
Employee[] staff;
Clearly, the statement:
staff[i].setSalary(100000);
fails in case staff[i] is a programmer. The statement:
staff[i].setSalary(150000);
succeeds if staff[i] is an executive, but fails if staff[i] is an ordinary employee.
Paradigms (Computational Models)
Different
observers will not perceive the same physical evidence in the same way unless
their linguistic backgrounds are quite similar.
Benjamin Lee Whorf
Language, Thought, and Reality
Some
accepted examples of actual scientific practice ... provide models from which
spring particular coherent traditions of scientific research.
Thomas S. Kuhn
The Structure of Scientific Revolutions
When
all you have is a hammer, everything looks like a nail.
Unknown
A Taxonomy of Computational Models
Although originally intended as a classification scheme for computer architectures, Treleaven and Lima's taxonomy [TRE] is perhaps better suited to computational models in general and programming languages in particular.
According to the scheme, each computation model can be classified according to its sequence control mechanism: Control-Driven (CO), Data-Driven (DA), Demand-Driven (DE), and Pattern-Driven (PA); and its data control mechanism: Shared Memory (SH) and Message Passing (ME). Thus, there are eight possible combinations:
|
COSH |
COME |
|
DASH |
DAME |
|
DESH |
DEME |
|
PASH |
PAME |
Sequence Control Mechanisms
A sequence control mechanism determines the flow of control through a program.
Control-Driven (CO)
Control-Driven programs explicitly specify control flow through the use of control structures: blocks, selections, iterations, and escapes. These control structures can be visualized as flowcharts.
Data-Driven (DA)
Data determine the flow of control in Data-Driven programs. This frees the programmer to concentrate on defining data structures. Dynamic dispatch combined with polymorphism gives rise to Data-Driven mechanisms in Object-Oriented programs.
Assume a class called Company contains an array of references (or pointers) to Employee records:
class Company {
Employee[] staff;
int staffSize = 0; // = next available
slot in staff[]
// etc.
}
Several of the company methods contain a command that traverses the staff array, invoking the print() method of each employee:
for(int i = 0; i < staffSize; i++) {
staff[i].print();
}
Of course Employee is only the base of a hierarchy of Employee subclasses, each of which overrides a virtual print() method inherited from the Employee superclass:
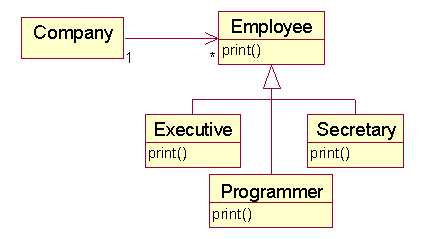
Each time the command:
staff[i].print();
is executed, different print() functions are called depending on the type of employee referenced. Thus, it is the employee object that determines the flow of control, not the programmer. This is the essence of Data-Driven programming.
At this point it might be instructive to contrast Data-Driven Programming with Control-Driven Programming. Without polymorphism and dynamic dispatch, programmers would need to replace the body of our for-loop with a multi-way conditional that explicitly determines the type of each employee, then performs an explicit downcast so that the correct variant of print() will be called. (At least Java's instanceof operator prevents us from having to provide our own type tags):
for(int i = 0; i < staffSize; i++) {
if (staff[i] instanceof Executive) {
((Executive)staff[i]).print();
} else if (staff[i] instanceof
Programmer) {
((Programmer)staff[i]).print();
} else if(staff[i] instanceof
Secretary) {
((Secretary)staff[i]).print();
// etc.
} else {
staff[i].print(); // call
Employee.print()
}
}
The main problem with the Control-Driven approach is that the control mechanism always resides in the client of any hierarchy. Thus, extending the hierarchy requires risky and possibly extensive modification of the client's control mechanism. Notice that extending the hierarchy requires no change to the client code in the Data-Driven model.
Demand-Driven (DE)
Demand-Driven pipelines are described and compared to Data-Driven pipelines in [PEA2].
Lazy Evaluation as Demand-Driven Control
Haskell's "cons" operator (denoted by the infix colon operator) allows programmers to add new elements to the beginning lists:
0: [1, 2, 3] -- = [0, 1, 2, 3]
"pluto":[] -- =
["pluto"]
Cons is lazy in its second argument, which means we can define non-terminating recursive functions:
fromN n = n: fromN (n + 1)
Here's a call:
ints = fromN 0
Presumably, ints is the infinite list of all integers:
ints = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ... ]
We can use the head and tail operators to probe this list:
head(tail(tail(tail(ints)))) -- = 3
Actually, ints is a pair consisting of 0 together with a promise to call fromN(1):
= (0, {fromN 1})
Applying the tail() function three times forces the promise three times:
(0, (1, {fromN 2}))
(0, (1, (2, {fromN 3})))
(0, (1, (2, (3, {fromN 4}))))
Notice that fromN() is only called when there is a demand for its value. The recursion only unwinds itself far enough to meet the demand.
Of course conditional and short circuit evaluation can also be regarded as forms of Demand-Driven evaluation:
test?f():g()
f1() && f2() && f3()
Abstraction as Demand-Driven Control
In a larger sense, we can regard abstraction as a form of Demand-Driven programming. For example, the function definition:
int sum1To5() { return 1 + 2 + 3 + 4 + 5; }
doesn't actually evaluate its body, 1 + 2 + 3 + 4 + 5. This only happens when there is a demand for this value, which only happens when the programmer explicitly calls sum1To5().
Pattern-Driven (PA)
Pattern-Driven Programming in Haskell
Haskell allows programmers to define types as patterns. For example, an instance of the recursive Exp (Expression) type is any pattern that matches the Lit (literal), Add, or Mul patterns:
data Exp =
Lit Int |
Add Exp Exp |
Mul Exp Exp
Here are some examples of instances of the Lit pattern:
(Lit 3), (Lit -23), (Lit 0)
The expression:
3 * 5 + 2 * 9
could be represented by the pattern:
exp = (Add (Mul (Lit 3) (Lit 5)) (Mul (Lit 2) (Lit 9)))
We can define an evaluation function as several branches, each parameterized by a pattern:
eval (Lit n) = n
eval (Add e1 e2) = eval e1 + eval e2
eval (Mul e1 e2) = eval e1 * eval e2
When the user attempts to evaluate exp:
eval exp -- = 33
The Haskell interpreter will use pattern matching to determine which branch of the eval function should be called.
Pattern-Driven Programming in Prolog
parent(homer, bart).
parent(homer, lisa).
parent(homer, maggie).
parent(marge, bart).
parent(marge, lisa).
parent(marge, maggie).
male(homer).
male(bart).
female(marge).
female(maggie).
femal(lisa).
spouse(homer, marge).
spouse(X, Y) :- spouse(Y, X).
wife(X, Y) :- spouse(X, Y), female(X), male(Y).
husband(X, Y) :- wife(Y, X).
child(X, Y) :- parent(Y, X).
father(X, Y) :- parent(X, Y), male(X).
sibling(X, Y) :- parent(Z, X), parent(Z, Y).
sister(X, Y) :- sibling(X, Y), female(X).
query/goals:
sister(X, bart).
sibling(X, bart), female(X).
parent(Z, X), parent(Z, bart), female(X).
parent(marge, lisa), parent(marge, bart), female(lisa).
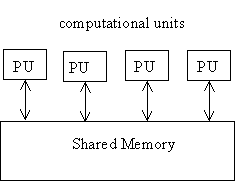
Data Control Mechanisms
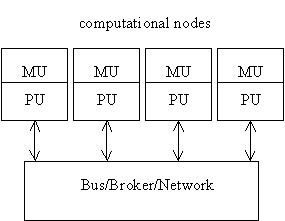
Message Passing
Broadcasting
Direct
1.1.1.1....1 Pipes/Streams
1.1.1.1....2 Interfaces
1.1.1.1....2.1 Asynchronous
1.1.1.1....2.2 Synchronous
Shared Memory/Shared Context
The simplest way for computational units to work together is through a collection of shared variables. As we have seen, these variables can be fenced off into scopes to control sharing: public, package, protected, private, scope, sub-scope, etc.
Computational Models
COSH
COME
DASH
DAME
DESH
DEME
PASH
PAME
The Big Four
Imperative Programming
Algorithms = control structures
explicit vs. implicit control
maybe this improves on [TRE]?!
Expression vs. Declaration vs. Command-Oriented.
Programs as finite state machines
Algorithms + Data Structures = Programs
The semantic gap refers to the complexity gap between the semantics of a high-level programming language, L, and the operational semantics of the underlying machine, M, that must execute L programs. Until compiler technology improved in the 1980s, the semantic gap was by necessity, small. Thus, high-level languages like C, FORTRAN, and Pascal, tended to reflect rather than hide the underlying structure of the hardware: data structures were abstractions of memory and the functions that updated these data structures were abstractions of processors.
This arrangement was fine as long as the solution to a problem looked like a computer. On the other hand, solutions to many problems do look like computers, or at least networks of finite state machines.
Structured Programming
Pascal
Object-Oriented Programming
Programs = Virtual Worlds
Encapsulation
Objects are the building blocks of Object-Oriented programs. An object is a component that encapsulates private variables (state) and receives messages (behavior). When an object receives a message, it searches a dispatch table for a corresponding message handler called a method. A method may access or update the encapsulated variables. A method may also send messages to other objects.
Classes and Subclasses
In class-based Object-Oriented languages, each object is an instance of some template called a class. The class of an object determines the types of the object's encapsulated variables, the types of messages it can receive, and the methods that handle these messages.
Classes are often confused for types, although there is a subtle distinction, namely that the type of an object only determines the types of its variables and messages, but not its methods:
class = type + methods
type = variable types + message types
New classes can be created from existing classes by extension:
class A { ... }
class B extends A { ... }
class C extends B { ... }
The subclass relationship:
X is a subclass of Y or X <: Y
is the transitive closure of the extends relationship. Thus, in the previous example we can infer:
C <: A
Inheritance
When an object receives a message it doesn't understand, the message can sometimes be handled by a method of some pre-designated parent object through either an inheritance or a delegation mechanism.
For example, assume:
C <: B <: A
An instance of class C inherits the methods of classes B and A, and can therefore handle messages it wasn't explicitly programmed to handle.
Polymorphism
Object-oriented languages support subclass polymorphism, which means an instance of class B can appear in any context where an object of class A was expected, when B is a subclass of A. To put this another way, if we make a distinction between the type and class of an object, then while an object is only an instance of one class, it can belong to many types (hence the term "polymorphism"). Namely, if an object belongs to type B, and if B <: A, then the object also belongs to type A.
Dynamic Dispatch
Finally, most Object-Oriented languages support some form of dynamic dispatch, which means the method used to handle a message is determined at runtime, by the object receiving the message, rather than by the compiler at compile time, which only knows the context where the object will appear.
Functional Programming
Programs = mathematical functions
Declarative Programming
Algorithms = Logic + Control
Programs as Rules
The holy grail of programming has always been automatic programming: the idea of replacing programmers with programs. Thus, instead of submitting a program specification to a programmer, customers submit their specifications to programs that "compile" specifications into provably correct programs.
Of course customers must take more care in writing specifications. In practice, the job of writing a good specification can be more difficult than the job of writing a program. In the end, the customer must hire the programmer to write the specification.
The difference between a program and a specification is that a specification is declarative in nature, while a program is imperative in nature. A pro
One way to prove a logical statement, A, is to show that it is impossible to refute A. Refutations are counterexample searches. Like other types of searches, counterexample searches can be conducted by computers. If all possible ways of finding a counterexample for A fail, then A must be valid.
We can turn this around. Suppose we view A as the specification of a solution to a problem-- for example, sorted(L1, L2) might describe what it means for list L2 to be the sorted version of list L1. If vals is a particular list, then we can ask a computer to refute the statement not sorted(vals, Y). The refutation should produce the sorted version of vals as a counterexample.
Y = vals'
Thus, we can view formal proofs (or rather refutations) as a form of computation, and programs as problem specifications.
Logic Programming
Prolog
References
[TRE] Treleaven, P.C. and Lima, G.I.; Future Computers: Logic, data flow, ..., control flow?; Computer, 17(3) 47-57.