10. Finite State Machines
Simple systems can be modeled as finite state machines (FSM). An FSM, M, has six components:
M = <Q, E, A, F, s, trans>
where:
Q = state space = a finite set of possible states
E = event space = a finite set of possible (input) events
A = action space = a finite set of possible (output) actions
F = a subset of Q = the set of possible final states
s = an element of Q = the start state
trans:QxE->QxA = the state transition function
At any moment one state of M is designated as the active state. The identity:
trans(q, e) = (p, a)
means:
If q is the active state of M, and if event e occurs, then p becomes the active state of M and action a is taken.
We can represent this situation graphically as:
![]()
Acceptance
We can extend the transition function to a function of the form:
TRANS:E*->Q*xA*
where
X* = all sequences of members of X.
Assume x, y, and z are events; u, v, and w are states; and a, b, and c are actions. Also assume:
trans(s, x) = (u, a)
trans(u, y) = (v, b)
trans(v, z) = (w, c)
Then xyz is a sequence of events in E*, and:
TRANS(xyz) = (suvw, abc)
In other words, given a sequence of input events, xyz, M transitions from its start state, s, to u, then v, then w, and performs the output actions a, b, and c.
We say that M accepts (or recognizes) xyz if w is a final state. That is, if w is in F.
(Readers familiar with the theory of finite automata and regular languages may recognize finite state machines as Mealy Machines.)
Transitions without Actions
We allow for a special no-op action in A. If
trans(q, e) = (p, no-op)
then we draw:
![]()
Completion Events
In case state q represents a task, then "q complete" is a member of E, and if
trans(q, "q complete") = (p, no-op)
we draw:
![]()
The Error State
Every FSM has an implicit error state. If the active state of M is q, and if event e occurs, and if:
trans(q, e) = undefined
then we can interpret this to mean:
trans(q, e) = (error, no-op)
Once in the error state there is no escape:
trans(error, e) = (error, no-op) for all e
FSM Diagrams
An FSM, M, can be represented as a directed graph in which states are nodes and transitions are arrows. For example, the following diagram:
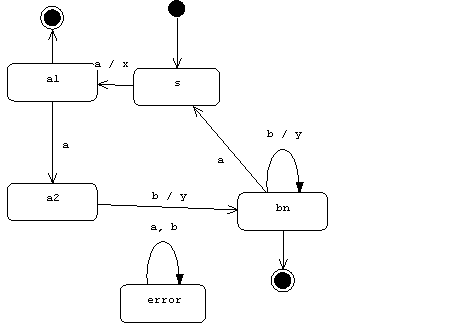
represents an FSM, M, where:
Q = {s, a1, a2, bn, error}
E = {a, b}
A = {x, y, no-op}
s = the start state
and where:
trans(s, a) = (a1, x)
trans(a1, a) = (a2, no-op)
trans(a2, b) = (bn, y)
trans(bn, b) = (bn, y)
trans(bn, a) = (s, no-op)
trans(i, j) = (error, no-op) for all other i and j
Notice that M accepts a. It also accepts all event sequences of the form:
aabb*
aabb*aa
aabb*(aaabb)*
aabb*(aaabb)*aa
For example:
TRANS(aabbbaa) = (sa1a2bnbnbnsa1, xyyyx)
In other words, if the user inputs the event sequence aabbbaa, then M produces the output xyyyx and ends up in the final state a1.
An Interpretation
Although we will see that a wide range of systems can be modeled by FSMs, it might be useful at this point for the reader to think of using an FSM to specify the behavior of an application, App, without specifying the internal structure of App.
Specifying the behavior of App means describing what actions App will perform in response to various input events. (This is just the old stimulus-response model from Behavioral Psychology applied to systems instead of rats!) Typical examples of input events are:
left mouse button clicked
q key pressed
"Print" menu item selected
input number
Typical examples of actions are:
display result
compute average of inputs
display file selection dialog box
Although our FSM doesn't specify the internal structure of App, it does recognize that behavior of App depends on its internal state (which is beginning to sound more like Cognitive Psychology rather than Behavioral Psychology). With this in mind, the FSM defines a finite set of abstract internal states. Examples might include:
document saved
document modified
first argument specified
result computed
A sequence of input events is accepted by App if they specify a complete a complete task performed by App.
Examples
Sequential Circuit Specification
A sequential circuit is an IC (= integrated circuit = computer chip) with a small amount of internal memory. (An IC without internal memory is called a combinational circuit.) We normally specify the behavior of an IC by a function of the form:
f(pin-in) = pin-out
where pin-in and pin-out are bit sequences.
This sort of specification is adequate for combinational circuits, but for a sequential circuit the output of f depends on its input and the contents of its memory. Furthermore, the contents of its memory may change when f is called.
If we think of all possible memory configurations of a sequential circuit as its state space, all possible pin-in sequences as its event space, and all possible pin-out sequences as its action space, then we can model sequential circuits using FSMs.
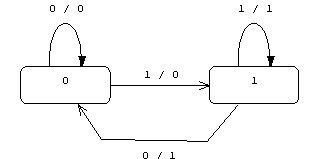
The simplest sequential circuit is a Flip-Flop. It has a 1
bit memory. Input events are 1 and 0, and output actions are 1 and 0.
Recognizing Tokens
The set of all legal numbers forms a regular language which is recognized by the following FSM:
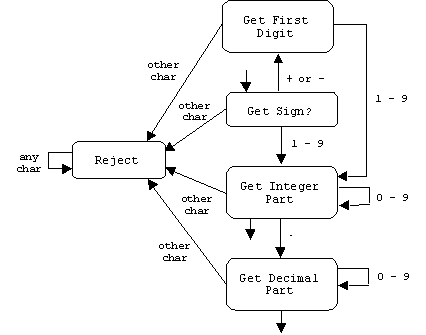
We can use this FSM to generate a scanner algorithm for recognizing legal numbers.
Lifecycle Models
An FSM can be used to represent the lifecycle of an object:
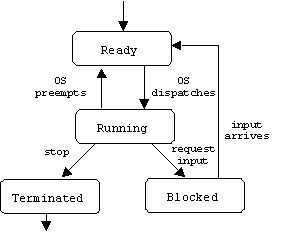
Specifying Workflows
An FSM can be used to represent a process, protocol, or workflow. In this case the states represent activities and transitions are often not labeled by events. This is because the event is implicitly understood to be the completion of the activity represented by the source state. We call such FSMs activity diagrams.
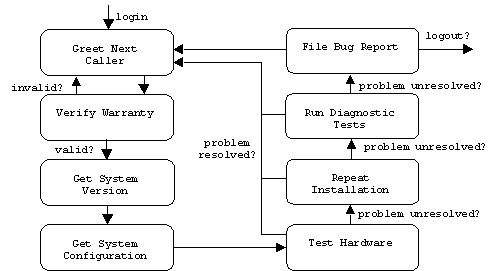
Specifying Applications/Elaborating Use Cases
A use case can be interpreted as an FSM. In this case events are actor messages. Transitions may cause messages to be sent from the system to the actor and may cause certain internal actions to be performed.
Example:
A computer game allows a hero, h, to navigate a maze looking for a treasure, t:
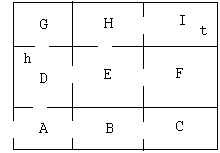
The basic messages (input events) the actor may send are up, down, right, and left:
S = { U, D, L, R }
States have the form:
Hero h is in room D
Which we simply abbreviate as D.
We can describe the behavior of the game with an FSM:
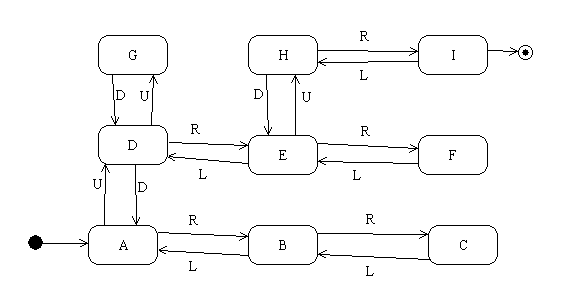
For example:
TRANS(UDRLURUR) = ADABADEHI
which, if this is the actor's complete message sequence, is a win.
Advanced FSM Features
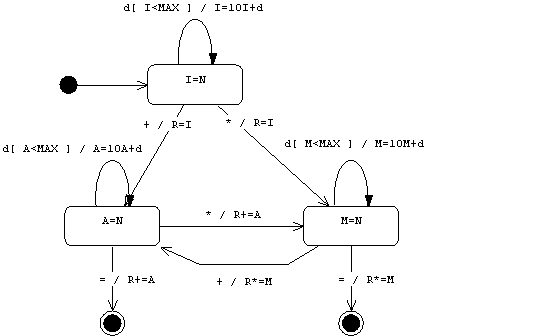
Conditional Transitions (Branch and Merge)
Transitions can be conditional and parameterized:
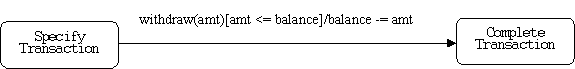
For example:
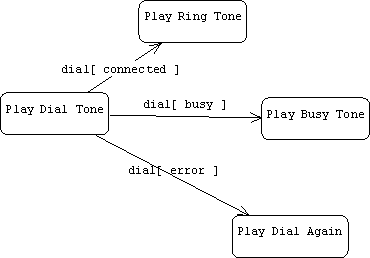
We can also use forks to show conditional transitions:
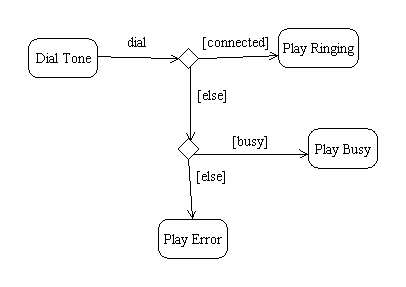
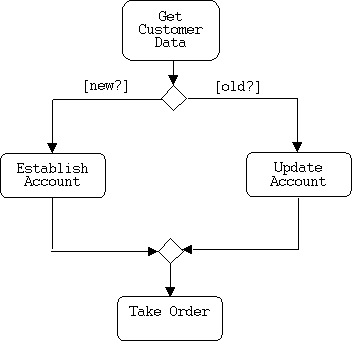
The opposite of a branch is a merge:
Concurrent FSMs
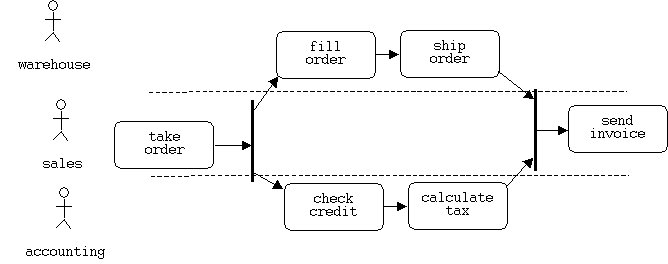
In our original definition, only a single state of an FSM was active at any given moment. Several states can be simultaneously active in a concurrent FSM. We use forks and joins, also called synchronization bars to show simultaneous activations or deactivations, and swim lanes to identify which processor or actor a given state is assigned to:
State Diagram for a Calculator
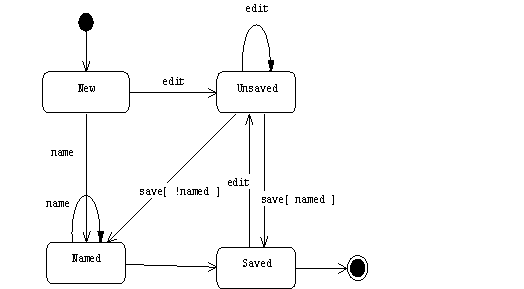
State Diagram for a Word Processor Document