Parser Combinators
Compiler-Compilers
A compiler-compiler is a program that transforms a grammar, G, into a parser for G:
Parser parser<G> = cc(G);
There are several famous examples of compiler-compilers: YACC and ANTLR.
Parser Combinators in Scala
Recall that a CFG rule has the form:
VARIABLE ::= PATTERN1 | PATTERN2 | ... | PATTERNn
A pattern can be a regular expression, a variable, or a composite pattern built from simpler patterns using quantifiers and operators:
PATTERNa~PATTERNb
PATTERNa|PATTERNb
PATTERN+
PATTERN?
Scala comes with a parser library that interprets parsers as functions that transform strings into trees:
Tree someTree = parser(someString)
The above operators and quantifiers are interpreted as higher-order functions called combinators. (Scala supports lambdas, functional programming, and higher-order functions.) Combinators combine simple parsers into more complex parsers.
For example, consider the grammar:
EXP ::= NUMBER~OPERATOR~EXP | NUMBER
If we think of NUMBER and OPERATOR as names of functions that parse strings of digits and individual operator symbols, respectively, then we can interpret the rule as the definition of a recursive function named EXP.
It might be helpful to rewrite the rule using prefix notation:
EXP ::= alt(seq(NUMBER, seq(OPERATOR, EXP)), NUMBER)
Where:
Parser alt(Parser p1, Parser p2) // creates a parser for p1 | p2
Parser seq(Parser p1, Parser p2) // creates a parser for p1 ~ p2
Parser rep(Parser p) // creates a parser for p+
Parser opt(Parser p) // creates a parser for p?
Parser regEx(String regexp) // creates a parser for regexp
Thus the CFG rules for a language not only specify the syntax of the language, they also define the parser for the language.
More details can be found here: Parsing in Scala.
Parser Combinators in Java
The inclusion of lambdas in Java 8 means that we can imitate the Scala parser library in Java.
The ComboParsers project consists of a single package called parsers. The package will implement and test the classes described below.
Result Trees
Instead of trees, our parsers return objects called results:
class Result { ... }
A result is a tree but with a list of unseen tokens—tokens that haven't been parsed yet. Thus, a result can represent a partial result: the tree so far plus tokens that still need to be parsed. As such, a result is both the input of a parser and the output:
// converts partial results into less partial results:
Result parser(Result r)
Result Subclasses
Our combinators create parsers that specialize in parsing options (?), concatenations (~), choices (|), iterations (+) and literals (strings). It's useful to define subclasses of Result to represent the outputs of these combinators.
Here's a UML diagram:
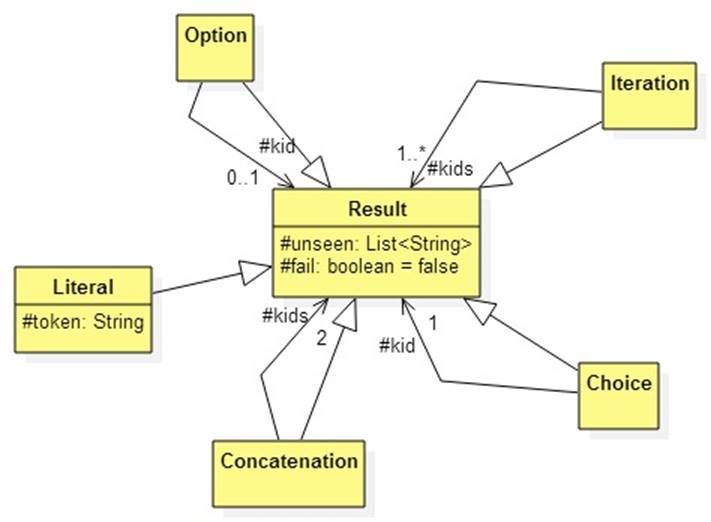
Except for literals, which will be the leaves of our trees, each subclass has 0, 1, 2, or many "kids". We think of an instance of these classes as parent nodes in our trees.
If a parsing error is encountered, then the fail flag is set to true. Failed results are not further parsed, instead they are passed back to the testing function for analysis.
Here's the complete code for the Result class:
public class Result {
protected List<String> unseen; //
unprocessed tokens
protected boolean fail; // parser error
//# unseen tokens
public int pending() { return
unseen.size(); }
public Result(String s, String regEx) {
fail = false;
String[] a = s.split(regEx);
unseen = new
ArrayList<String>();
for(int i = 0; i < a.length; i++)
{
unseen.add(a[i]);
}
}
public Result(String s) {
this(s, "\\s+");
}
public Result() {
unseen = new ArrayList<String>();
fail = false;
}
public String toString() {
return "[fail = " + fail +
"; unseen = " + unseen + "]";
}
}
Normally results are created by combinators. The exception is the first result. That is created from the initial string to be parsed. The constructor breaks the string into a list of tokens separated by some separator that matches a specified regular expression (usually the separators are white spaces), and sets unseen to this list. Basically, this is the empty tree and all of the tokens have yet to be seen.
Parsers
Recall that UnaryOperator<T> is an interface defined in java.util.function. This is the type of all lambdas (function-objects) that have domain = range = T.
An instance of the Parser class both implements this interface (with domain = range = Result) and encapsulates a lambda of this type. The required apply method simply delegates to the encapsulated lambda:

In effect, Parser is a wrapper for lambda parsers. This not only shortens our combinators, but it also allows combinators to define recursive parsers. For example:
S ::= seq(regEx(zero), S) // S ::= zero S
Combinators
Combinators is a utility class (all members are static):

Here's a partially completed implementation:
public
class Combinators {
// returns p1 | p2
public static Parser alt(Parser p1,
Parser p2) {
Parser parser = new Parser();
parser.setParser(
result->{
if (result.fail)return result;
Choice answer = new Choice();
answer.choice = p1.apply(result);
if (answer.choice.fail) {
answer.choice = p2.apply(result);
}
if (answer.choice.fail) return answer.choice;
answer.unseen = answer.choice.unseen;
return answer;
});
return parser;
}
// returns p1 ~ p2
public static Parser seq(Parser p1,
Parser p2) {...}
// returns p+
public static Parser rep(Parser p)
{...}
// returns p?
public static Parser opt(Parser p)
{...}
// returns p = regExp
public static Parser regEx(String
regex) {...}
// etc.
}
The
alt combinator creates a parser wrapper, sets the encapsulated parser to a
lambda, then returns the result. This is essentially how all of the combinators
work.
The
lambda takes a result (of type Result) as input. If the result has already
failed, it is immediately passed on. Otherwise, a Choice object is created
named answer. If all goes well, this will be the value returned by the lambda.
This makes sense since the output of alt will be a parser for parsing choices
of the form p1 | p2. In my implementation a choice has a single kid which I
call choice.
The
parser attempts to parse the result using p1. If this fails, then the parser
attempts to parse the result using p2. If this fails, then the failed result is
immediately passed on. Otherwise the unseen tokens of the answer are set to the
unseen tokens of the choice and the answer is returned.
result->{
if (result.fail)return result;
Choice answer = new Choice();
answer.choice = p1.apply(result);
if (answer.choice.fail) {
answer.choice = p2.apply(result);
}
if (answer.choice.fail) return
answer.choice;
answer.unseen = answer.choice.unseen;
return answer;
}
To
put it simply, the p1|p2 parser attempts to parse the unseen tokens of result
using p1, of this fails, the p2 is used.
Example
To use combinators, start with a CFG. For example:
EXP ::= NUMBER~OPERTOR~EXP | NUMBER
OPERATOR ::= \+|\*
NUMBER ::= [0-9]+
Next, define a utility class that creates parsers for each rule:
public
class ExpParsers {
public static Parser number =
Combinators.regEx("[0-9]+");
public static Parser operator =
Combinators.regEx("\\+|\\*");
public static Parser exp = new
Parser();
static {
exp.setParser(
Combinators.alt(
Combinators.seq(
number,
Combinators.seq(operator,
exp)),
number));
}
}
Here's a simple test driver:
public static void testExpParsers() {
String s = "42";
test(ExpParsers.number,
s);
s = "29z";
test(ExpParsers.number,
s);
s = "*";
test(ExpParsers.operator,
s);
s = "-";
test(ExpParsers.operator,
s);
s = "42 + 91 * 13 + 2";
test(ExpParsers.exp, s);
s = "123";
test(ExpParsers.exp, s);
s = "15 * 6 - 10";
test(ExpParsers.exp, s);
}
My test function prints the string, makes an initial result, parses it to a tree, then prints the tree and the number of pending tokens:
public static void
test(Parser p, String s) {
System.out.println("s = " + s);
Result tree
= p.apply(new Result(s));
System.out.println("tree = " + tree);
System.out.println("pending = " + tree.pending());
}
Here's the output:
s = 42
tree = <42>
pending = 0
s = 29z
tree = fail
pending = 1
s = *
tree = <*>
pending = 0
s = -
tree = fail
pending = 1
s = 42 + 91 * 13 + 2
tree = [ | [<42> ~ [<+> ~ [ | [<91> ~ [<*> ~ [ |
[<13> ~ [<+> ~ [ | <2>]]]]]]]]]]
pending = 0
s = 123
tree = [ | <123>]
pending = 0
s = 15 * 6 - 10
tree = [ | [<15> ~ [<*> ~ [ | <6>]]]]
pending = 2
The output is not very enlightening. Each of my Result subclasses has a toString method that prints something of the form:
[op kids]
where op = +, |, ~, ? indicating the type of result, and any kids. The exception are literals, which are bracketed by angle braces: <42>, <+>, etc. Never the less, each result is a tree which could be navigated by any program interested in executing or translating trees.
To Do
Create a utility class called DemoParsers. This class should contain parsers (created using your combinators) for the following grammars:
NUMBER ::= [1-9]+
NAME ::= [a-zA-Z][a-zA-Z0-9]*
BOOLE ::= true | false
OPERATOR ::= && | \|\| | \+ | \* | !
TERM ::= NAME | NUMBER | BOOLE
PRODUCT ::= TERM | TERM~(OPERATOR~TERM)+Create a test driver that tests all of
these grammars on both good and bad input strings.
Submit your code and the output of your tests.