CALab
Cellular Automata
Cellular Automata (CAs) were introduced in the late 1940s by two mathematicians: Stanislaw Ulam and John Von Neumann. They were motivated by the question: could machines reproduce? In other words, could we build a machine that builds a copy of itself when switched on?
A CA is an infinite grid of cells. Each cell, C, is a simple "machine" that might represent the behavior of a region, household, individual, etc. At any time t, C is in one of N states. States can be anything: temperature, wealth, political affiliation. At time t + 1, C may transition into another state. The new state is determined by the states of C and its neighbors at time t.
While the behavior of each individual cell is necessarily simple, we might wonder if the behavior of the CA taken as a whole might be complex and interesting. It turns out that the answer is yes. In fact, it is theoretically possible to compile any program into a CA. This should not be too surprising considering that the human brain can be viewed as a CA in which neurons play the role of cells.
The CA Update Loop
CALab allows users to create CAs, but with the restriction that the grid is finite but wraps. In other words, a cell on an edge is neighbors with the corresponding cell on the opposite edge. The CA lifecycle consists of three phases: observe, interact, and update.
void updateLoop(int cycles) {
for(int cycle = 0; cycle < cycles;
cycle++) {
observe();
interact();
update();
}
}
During the observation stage each cell gathers information about the states of its neighbors. During the (optional) interaction phase each cell interacts with a random neighbor. Types of interactions include bargaining, fighting, playing a game, etc. In the update phase each cell changes its state according to information gathered in the previous phases. Different CAs and different cell types within a CA may have different rules for how to update themselves.
Conway
The Game of Life was invented by British mathematician John Conway and was popularized in Martin Gardner's Mathematical Games column in the October 1970 issue of Scientific American.
The Game of Life is not actually a game. It is a powerful family of CAs. Each cell is in one of two states: 0 = dead or 1 = alive. During the observation phase each cell computes the number of living neighbors. This is called the ambience of the cell. The ambiance of a cell is a number between 0 and 8:
0 <= ambience <= 8
T01 and T10 are user-defined subsets of the set of all possible values for ambience:
{0 1 2 3 4 5 6 7 8}
Cells don’t interact in Conway’s game. During the update
phase a dead cell is reborn (transitions from state 0 to state 1) if its
ambience is in the set T01 and a living cell dies (transitions from
state 1 to 0) if its ambience is in the set T10. Otherwise the state
of the cell doesn't change. Users can experiment with different values for T01
and T10. They don't need to be disjoint, and one or both can be
empty. In
T01 = {3}
T10 = {0 1 4 5 6 7 8}
In other words, a cell dies if it's too lonely (0 or 1 living neighbors) or too crowded (4 or more living neighbors), and a cell is reborn if it has exactly three living neighbors.
In the following screenshot of CALab red cells are dead and green cells are alive. Each cell displays its current ambience.
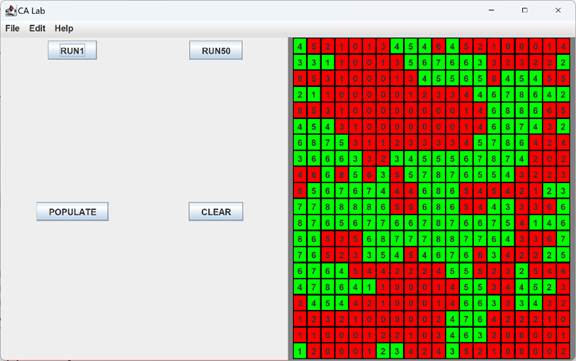
The button on the control panel (which are also options under the Edit menu) work as follows:
RUN1: calls grid.updateLoop(1)
RUN50: calls grid.updateLoop(50)
POPULATE: calls grid.repopulate() which sets the state of each cell to a random
value
CLEAR: calls grid.clear() which sets the state of each cell to an initial
value.
Applications
Most applications of CAs are simulations of social systems such as markets, cities, and organizations. Here are a few:
· Epstein's Civil Disobedience Model
CALab Design
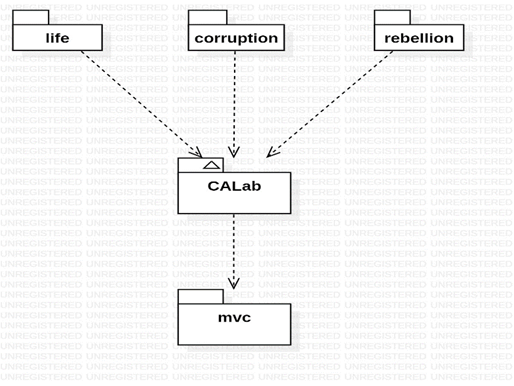
CALab is a customization of the mvc framework. It is itself a framework for creating different types of CAs:
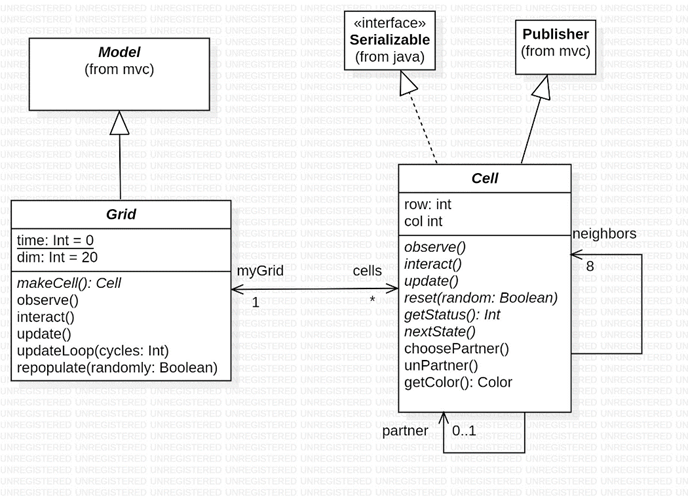
In CALab the CA is represented by the Grid class, which contains an NxN grid of cells:
Notice:
1. Cell and Grid are abstract classes. The observe, interact, and update methods in the Cell class are abstract because different types of cells will have different ways of implementing them. So how does a grid know what types of cells to create? It doesn’t. So it’s makeCell method is abstract and will need to be implemented in a subclass. (makeCell is an example of an abstract factory method.)
2. A cell has eight neighbor cells. (Remember that the grid is wrap-around. Topologically, the grid is a torus or hollow donut. See why?). During the interaction phase—if there is one-- a cell selects a random (partnerless) neighbor as a partner and becomes the partner’s partner. However, this can fail. For example, it can happen that all of the neighbors already have partners. Always check to make sure partner != null before interacting with it. At the end of the interaction phase all partnerships dissolve. More succinctly, cell may have 0 or 1 partner.
3. A cell maintains a link to its grid. This is useful when the grid provides services or data to the cells.
4. The grid is the mvc model. This means that the grid is a serializable publisher. But saving the grid to a file means saving its cells to a file, so cells also need to be serializable. There could be applications where some UI component needs to be notified of changes in one particular cell, so I’ve made cells publishers as well.
5. The grid’s observe method calls the observe method of each cell, then notifies subscribers. Similarly the interact method calls the interact methods of each cell and the update method calls the update method of each cell.
6. Most applications of CAs are social simulations—cities, organizations, markets, etc,-- Simulations often need a time keeper that tracks how many cycles have been executed. For this reason the grid maintains a static time variable that it updates in the updateLoop.
GridView
The presentation layer of CALab is similar to the model layer. A GridView consists of an NxN grid of CellViews. The GridView’s model is the Grid and each CellView is associated with one Cell.
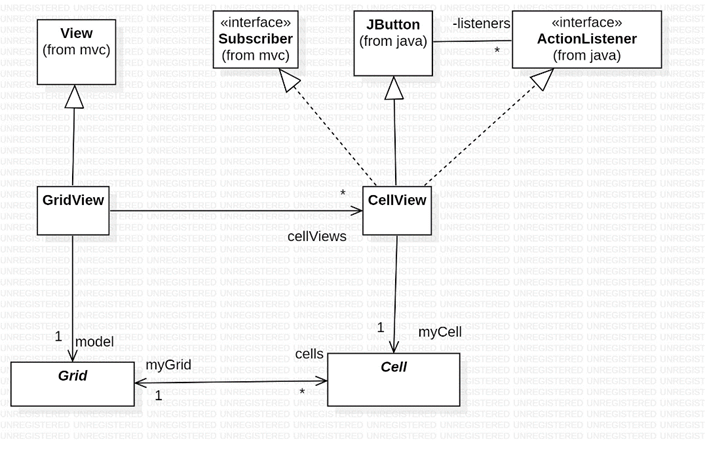
CellViews are JButtons that listen to themselves! Each time a user clicks a cell view it manually advances the associated cell to its next state:
public void actionPerformed(ActionEvent e) {
myCell.nextState(); // changes the
state of myCell
setBackground(myCell.getColor());
setBorder(BorderFactory.createLineBorder(Color.black));
setText("" +
myCell.getStatus());
}
Where nextState, getColor, and getStatus are abstract methods in the Cell class.
The CellView update method is almost identical, but doesn’t call nextState.
CALab
Implementation
A partial implementation can be found here: Grid.java.
A few comments:
1. I decided that grids should be composites rather than aggregations of cells. What does this mean? There are two types of collections: composites and aggregates. Components (e.g. cells) can be added and removed from aggregate collections but not from composite collections. (For example, the employees of a company is an aggregate collection, but the chips in a computer is a composite collection.) Consequently, all changes to a grid are simply changes to the states, not the identities, of its cells. Composites are more efficient than aggregates but its components can’t be shared and copying a composite requires copying its components.
2. I modified update loop by changing the observe-interact-update cycle into an interact-update-observe cycle and called observe once outside of the for-loop to initialize ambience. Doing it this way means the ambiences displayed in the grid view will always be current rather than the ambiences from the previous cycle.