Scala Parser
Combinators: An Example
Video
The following notes is explained in this video: Scala Parser Combinators.
P.S. Please forgive the excruciatingly loud keyboard in this video. I have heavy fingers and the mic is next to the keyboard.
SOP
SOP is a language for computing sums of products of numbers. Here's a sample session with the SOP interpreter:
-> 3
value: 3.0
-> 3.14
value: 3.14
-> -2.78
value: -2.78
-> 2 + 3
value: 5.0
-> 2 * 3
value: 6.0
-> 2 + 3 * 5
value: 17.0
-> (2 + 3) * 5
value: 25.0
-> quit
bye
Notes
· There are three types of expressions users can type: numbers, sums, and products.
· Signed numbers are understood.
· Products have precedence over sums,
· unless the sum is in parentheses.
The SOP Console
Here's the console user interface for the interpreter:
Notes
· Console is a singleton.
· Repl stands for read-execute-print-loop.
· The execute method parses the user's input into an expression, executes the expression, then returns the corresponding value as a string.
· As a side-effect, the untransformed output of the parser is displayed.
SOP1 Expressions
For contrast, we'll do two versions of SOP: SOP1 and SOP2.
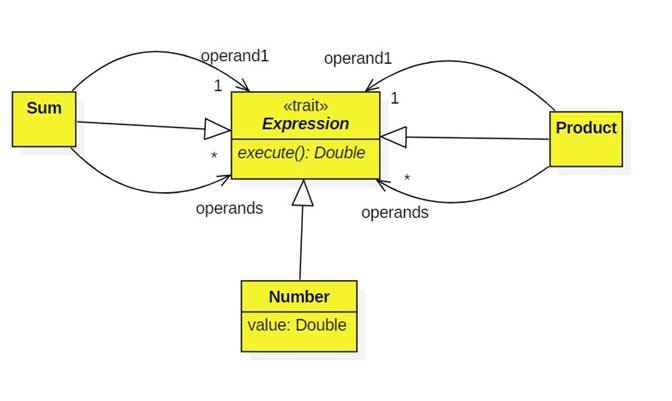
Here's a UML diagram of the SOP1 expression hierarchy:
And here's the code:
Notes
· For Sum and Product operand1 represents the first number to be added or multiplied, and operands is a list of any additional numbers to be added or multipled.
· Number is a wrapper for Scala Double.
· Note the cool way map is used to execute and combine operands.
SOP1 Grammar
Here's an EBNF grammar for SOP1:
expression ::= sum
sum ::= product ~ ("+" ~ product)*
product ::= term ~ ("*" ~ term)*
term ::= number | "(" ~ expression ~ ")"
number ::= """(\+|\-)?[0-9]+(\.[0-9]+)?""".r
Notes
· Recall that formal grammars are used to specify the syntax (i.e., grammar) of programming languages.
· EBNF = Extended Bachus-Naur Form.
· We can read our grammar as follows:
An expression is a sum.
A sum is a list of one or more products separated by + signs.
A product is a list of one or more terms separated by * signs.
A term is a number or an expression in parentheses.
A number is an optional + or – sign followed by a sequence of digits optionally
followed by a dcimal point and more digits
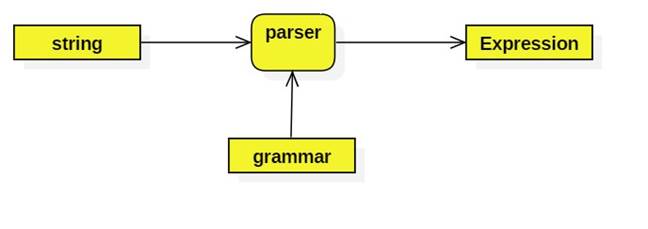
· A parser is a function that uses a grammar to transform strings into expressions:
· I'm pretty sure this grammar is unambiguous. Recall that an ambiguous grammar is one that is open to multiple parsings of an input string.
· For example, does "2 + 3 * 5" parse to (2 + 3) * 5 or 2 + (3 * 5)? Our grammar parses it to the latter, which also insures that multiplication takes precedence over addition.
· Regular expressions can be incorporated into grammars. This was done to specify the format of a number.
Here's the Scala equivalent of our grammar:
Let's analyze a single parser in this class:
def sum:
Parser[Expression] = product ~ rep("+" ~> product) ^^ {
case p ~ Nil => p
case p ~ prods => Sum(p, prods)
}
Notes
· Think of sum: Parser[Expression] as shorthand sum: String=>Option[Expression]. In other words, sum is a parser that transforms strings into expressions or fails if the string contains syntax errors.
· product is also a parser.
· rep("+" ~> product) is the Scala way of writing ("+" ~> product)*
· The arrow head tells the parser to check for the + sign, but not to include it in the output.
· Here's the mind blower: rep and ~ are combinators that take simpler parsers as inputs and return more complicated parsers as outputs.
· Raw parsers (the part before the ^^ sign) return tree-like structures that need to be transformed (that's the meaning of ^^) into SOP1 expressions.
· In our case the raw parser returns a product (p) possibly followed by a list of products, prods. (The output of rep is a list of products.) If the pist is empty, we return p, a product, otherwise we return a sum with p = operand1 and prods = operands.
SOP1 Session
Here's a sample session with SOP1 showing the untransformed trees:
-> 42
tree: Number(42.0)
value: 42.0
-> 2 + 3 + 4
tree: Sum(Number(2.0),List(Number(3.0), Number(4.0)))
value: 9.0
-> 2 * 3 * 4
tree: Product(Number(2.0),List(Number(3.0), Number(4.0)))
value: 24.0
-> 2 + 3 * 4
tree: Sum(Number(2.0),List(Product(Number(3.0),List(Number(4.0)))))
value: 14.0
-> quit
bye
Notes
Here's a tree representation of the tree generated by "2 + 3 + 4":
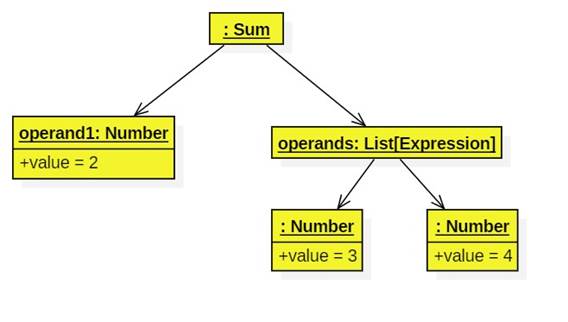
Here's the tree generated by "2 + 3 * 4":
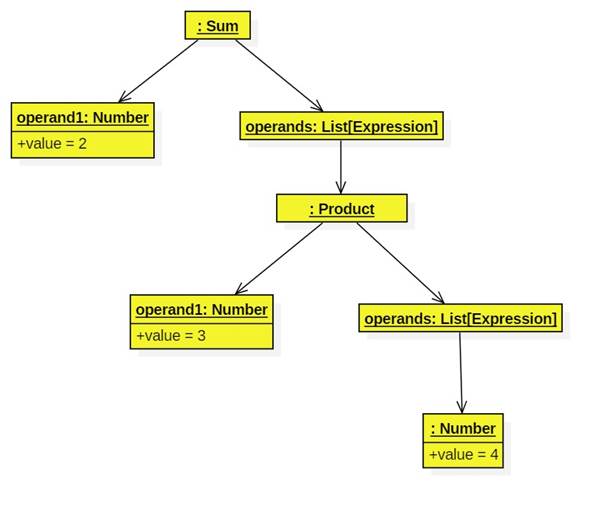
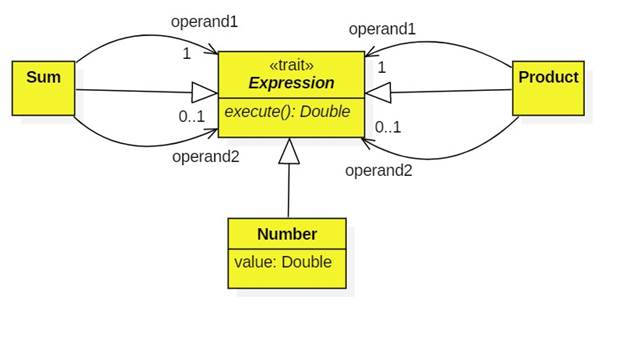
SOP2 Expressions
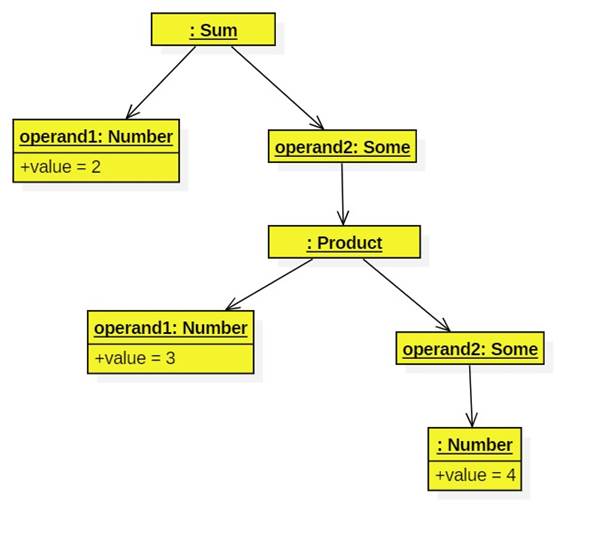
In SOP1 a sum is a list of one or more expressions. In SOP2 a sum is one or two expressions. Here's the class diagram:
Here's the code:
Notes
· How to indicate operand2 has multiplicity 0 or 1? Looks like an opportunity to use optional values.
· Note the use of match/case in execute.
SOP2 Grammar
Here's the EBNF grammar for SOP2:
expression ::= sum
sum ::= product ~ ("+" ~ expression)?
product ::= term ~ ("*" ~ expression)?
term ::= number | "(" ~ expression ~ ")"
number ::= """(\+|\-)?[0-9]+(\.[0-9]+)?""".r
Notes
· We can read our grammar as follows:
An expression is a sum.
A sum is a product possibly followed by a + sign followed by an expression.
A product is a term possibly followed by a * sign followed by an expression.
A term is a number or an expression in parentheses.
A number is an optional + or – sign followed by a sequence of digits optionally
followed by a dcimal point and more digits
Here's the Scala equivalent of our grammar:
Let's analyze a single parser in this class:
def sum: Parser[Expression] = product ~ opt("+" ~>
expression) ^^ {
case p ~ None =>
p
case p ~ Some(exp)
=> Sum(p, Some(exp))
}
Notes
· opt("+" ~> expression) is Scala's way of writing ("+" ~> expression)?
· opt generates an optional value: None or Some(exp).
· So our raw parser generates a product p followed either by None or Some(exp) where exp is the output of the recursive call to the expression parser.
· Note that the + sign is dropped.
Sample Session
Here's a sample SOP2 session:
-> 42
tree: Number(42.0)
value: 42.0
-> 2 + 3
tree: Sum(Number(2.0),Some(Number(3.0)))
value: 5.0
-> 2 * 3
tree: Product(Number(2.0),Some(Number(3.0)))
value: 6.0
-> 2 + 3 + 4
tree: Sum(Number(2.0),Some(Sum(Number(3.0),Some(Number(4.0)))))
value: 9.0
-> 2 + 3 * 4
tree: Sum(Number(2.0),Some(Product(Number(3.0),Some(Number(4.0)))))
value: 14.0
-> quit
bye
Notes
· Don't forget to change the console's parsers to Parsers2.
· Here's the tree generated by "2 + 3 * 4":