Type Systems

Types

A type consists of a domain of data values and a set of operations for manipulating these values:

Type = <Domain; Operations>

We write:

v:T

to indicate that value v is a member or instance of the domain of type T.

We can overload this notation and write:

T:Type

to indicate that T is a type.

(Is this really overloading or can we simply consider Type to be the type of all types!)

A type can be primitive or composite:

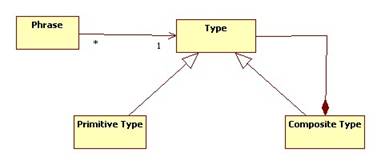
Examples of primitive types include:

int = <int; +, -, *, />
double = <double; +, -, *, />
char = <char>
Boolean = <{true, false}; &&, ||, !>

Examples of composite types include array types, classes, and interfaces.

Type Systems

A type system consists of:

1. a set of primitive types
2. a set of type constructors
3. a subtype partial ordering: T1 <: T2
4. an equivalence relationship: T1 = T2
5. Rules and axioms for type checking

Type Checking Rules

A rule has the form:

Assumptions
Conclusion

A rule with no assumptions is called an axiom.

The conclusions of several rules can form the assumptions of another rule, thus rules can be chained together to form derivation trees. Leafs of a derivation tree are axioms. The root is a theorem.

If we introduce a special error type, then deriving the conclusion:

e:Error

indicates that the expression e contains type errors.

There are four types of rules:

Formation rules

A formation rule shows how a composite type is created from component types using a type constructor.

Elimination rules

An elimination rule shows us how to extract components from an instance of a composite type.

Introduction Rules

An introduction rule shows us how to introduce new instances of a composite type.

Computation Rules

A computation rule shows us how the elimination rules are actually computed.

Example: The LISP++ Type System

Example: The Java Type System

Subtyping and Type Equivalence

We can express subtyping and type equivalence using rules.

For example, here are the axioms saying that subtype and equality are reflexive:

A <: A

A = A

Here are the rules saying that these two relationships are transitive:

A <: B, B <: C
A <: C

A = B, B = C
A = C

In addition, equality is symmetric:

A = B
B = A

Type equivalence refines the subtype relationship:

A = B
A <: B

Here is the subsumption rule:

v:A, A <: B
v:B

The contravariance principle says that for function types increasing the domain and or shrinking the range produces a subtype:

A <: A', B <: B'
A'->B <: A->B'

Type Equivalence

There are two kinds of type equivalence: structural and name equivalence. We can see this with a few examples.

Assume the following C declarations have been made:

class Date1 { int day, mont, year};
class Date2 { int day, mont, year};

Date1, Date2 are structurally equivalent (because they have the same fields), but not name equivalent.