Operator Overloading

Most programming languages discriminate against programmer-defined types. This segregation is so common place we have come to use the terms first class and second class types to refer to built-in types (like int, float, and char) versus programmer-defined types (like Employee, Sale, and Toaster). Some of the privileges commonly enjoyed by members of first class types include:

1. Compared and combined using infix operators like + and <.

2. Automatically converted to and from strings by I/O operators << and >>.

3. Automatically cast to other types by type system.

One of the goals of C++ was to obliterate the distinction between first and second class types. C++ programmers can endow their types with the privileges listed above to create the illusion that their types are seamlessly integrated into the language. The trick is that most C++ operator symbols like +, <, =, etc. are aliases for functions with names of the form operator+(), operator<(), operator=(), etc. Like any other functions, these can be overloaded by programmers.

Overloading Arithmetic Operators

A rational number (i.e., a fraction), for example ¾, consists of two integers: a numerator, 3, and a denominator, 4. We can represent rationals as objects encapsulating pairs of integers:

class Rational
{
int num, den;
// etc.
};

We want our new Rational type to have first class status. Most C++ operators are aliases for functions with names made from the keyword operator followed by the operator symbol. For example, * is an alias for the function operator*(). We can redefine these functions, thereby redefining the behavior of the associated operator.

In most cases we have two choices, the operator function can be a member function or a global function (which can be declared a friend, if necessary). For instructional purposes, we use the first approach with operator+(), and the second approach for the other operators.

class Rational
{
public:
Rational(int n = 0, int d = 1);
Rational operator+(const Rational& r) const;
friend Rational operator*(const Rational& r, const Rational& q);
friend Rational operator-(const Rational& r, const Rational& q);
friend Rational operator/(const Rational& r, const Rational& q);
friend bool operator==(const Rational& r, const Rational& q);
friend bool operator<(const Rational& r, const Rational& q);
private:
void reduce();
int num, den;
};

Before we define our operators we note that the constructor "normalizes" the numerator and denominator by calling a private support function called reduce():

Rational::Rational(int n /* = 0 */, int d /* = 1 */)
{
num = n;
den = d;
reduce();
}

For example, reduce() converts 6/-8 into –3/4, and –4/-2 into 2/1. It also generates an error if the denominator is zero:

void Rational::reduce()
{
if (den == 0)
error("denominator = 0");
int s = sign(num * den);
int n1 = abs(num);
int d1 = abs(den);
int q = gcd(n1, d1);
num = s * n1/q;;
den = d1/q;
}

The gcd() function was defined in a previous chapter. The sign() function returns –1 if the sign of its argument is negative, and 1 otherwise:

inline int sign(int n)

{

return n < 0? -1: 1;

}

Note the use of the conditional expression:

CONDITION?CONSEQUENT:ALTERNATIVE

where CONDITION, CONSEQUENT, and ALTERNATIVE must be expressions. Unlike the conditional statement:

if (CONDITION) CONSEQUENT; else ALTERNATIVE

the conditional expression produces a value (i.e., the value of CONSEQUENT or the value of ALTERNATIVE), hence can be used any place an expression is expected, for example as the argument of a return statement.

Here are the definitions of operator+() and operator*(). The algorithms are from standard Algebra books:

Rational Rational::operator+(const Rational& r) const
{
return Rational(num * r.den + den * r.num, den * r.den);
}

Rational operator*(const Rational& r, const Rational& q)
{
return Rational(q.num * r.num, q.den * r.den);
}

Note that operator+() only has one argument. The other argument is the implicit parameter. If r and q are rationals:

Rational r(1, 2), q(3, 4);

Then the expression:

r + q;

will be translated into:

r.operator+(q);

On the other hand, operator*() requires two parameters because it is not a member function. The good news is that the definition doesn't need to be qualified with the scope resolution operator. The expression:

r * q;

will be translated into:

operator*(r, q);

So what's the difference? Surprisingly, the following expressions evaluate to the correct answer:

r + 5; // produces ½ + 5/1 = 11/2

r * 5; // produces ½ * 5/1 = 5/2

How did the conversion of the integer 5 to the rational 5/1 happen? C++ noticed that a rational number constructor was available that would accept a single integer as input, and used this to perform the conversion. Thus the expressions were translated into:

r.operator+(Rational(5, 1));
operator*(r, Rational(5, 1));

The law of commutativity says a + b = b + a, so we should be able to evaluate the expressions:

5 + r; // error
5 * r; // produces ½ * 5/1 = 5/2

The second expression worked for the same reason r * 5 worked, however, C++ won't perform automatic conversions on the implicit parameter, hence the second expression failed. In the case of commutative arithmetic operators, the behavior of the operator*() global function is preferred over the behavior of the operator+() member function, but there are situations where the reverse is true.

Overloading Type Conversion Operators

We have seen that C++ will automatically convert integers into rationals by using the Rational constructor with second argument = 1. But what about converting rationals into reals? For example, ½ can be converted to 0.5. We could try to define a Rational constructor that takes a double as an input:

Rational::Rational(double d) { ??? }

but this is going the wrong way. It is converting doubles to rationals. Besides. mathematically this doesn't make sense because most real numbers are irrational.

It turns out the conversion operators are aliases for functions, too. For example, the expression:

double(42); // produces 42.0

translates to:

operator double(42);

If we define operator double() for rational numbers, the C++ will use this to automatically convert rationals to doubles. Note that operator double() always returns a double, so we don't need to declare a return type. (In fact, C++ won't allow us to declare a return type.)

class Rational
{
public:
operator double() { return double(num)/double(den); }
// etc.
};

We can now pass rationals to functions that expect doubles as inputs:

sin(Rational(1, 2)); // calls sin(0.5)

Overloading Insertion and Extraction Operators

We can move closer to our goal of making Rational a first class type by providing insertion and extraction operators. The expressions:

cin >> x;
cout << x;

translate to the expressions:

operator>>(cin, x);
operator<<(cout, x);

Because the first argument is always a stream, these functions must be global (why?). Also, these functions must return their first argument as an output to allow chaining:

cout << x << y << z;

Both functions alter their stream arguments, so this must be passed by reference. The extraction function also alters its second input, so this must be passed by reference, too. Here are the prototypes:

class Rational
{
public:
friend ostream& operator<<(ostream& os, const Rational& q);
friend istream& operator>>(istream& is, Rational& q);
// etc.
};

The insertion operator calls the integer and character variants of the insertion operator to print the numerator, slash character, and denominator:

ostream& operator<<(ostream& os, const Rational& q)
{
os << q.num;
if (q.den != 1) os << '/' << q.den;
return os;
}

As always, extraction is more complicated, because we must deal with the possibility that the extracted characters don't have the form of a rational number. When a user enters a rational number, we expect it to have the form a/b or a, where a and b are integers. Failure to meet any of these requirements should result in setting the input stream state to fail, and returning immediately. For example, the inputs 3/x, 3\5, and x/5 all result in a failed state. But what happens if the user types a single integer followed by some white space and a newline? We should accept this as a rational with numerator 1. We can use peek() to see if the next character is white space. Of course if the user enters 3 /5, this will be interpreted as 3/1 and the /5 will be left in the buffer:

istream& operator>>(istream& is, Rational& rat)
{
rat.den = 1; // for now
char slash; // should be '/'
is >> rat.num; // will it work?
if (is) // yes, last extraction succeeded
{
if (isspace(is.peek())) // if next char is white space
return is; // success, rat.den = 1
is >> slash >> rat.den; // will these work?
if (slash == '/' && is) {
rat.reduce();
return is; // success
}
}
is.setstate(ios::failbit); // put is in fail state
return is;
}

Safe Strings

Safe strings, also known as smart strings, encapsulate C strings (also known as dumb strings). A partial implementation follows, a complete implementation is given in another chapter. It is entirely for instructional purposes. Programmers should use the string class from the standard C++ library, instead. Features of the implementation are shown in boldface.

string.h

#include <cstring> // <string.h>
#include <iostream>
using namespace std;

class String
{
public:

String(char* s = 0);
String(const String& s) { copy(s); }
~String() { free(); }
String& operator=(String& s);
String& operator=(char* s);
char& operator[](int i);

bool operator==(const String s) const
bool operator!=(const String s) const
bool operator<(const String s) const
bool operator>(const String s) const
friend ostream& operator<<(ostream& os, const String& s);
friend istream& operator>>(istream& is, String& s);

friend String operator+(const String& s1, const String& s2);
friend String operator+(const String& s1, char * s2);
friend String operator+(const String& s1, char c2);
bool empty() const { return length == 0; }
int getLength() const { return length; }
char* getStr() { return str; }
operator char*() const { return str; } // automatic conversion

// etc.

private:

int length; // string length
char* str; // the encapsulated C string
void copy(const String& s); // must use pass-by-ref
void free() { if (str) delete[] str; }
};

string.cpp

The first constructor allows us to convert C strings into smart strings:

String::String(char* s /* = 0 */)
{
if (s == 0)
{
str = 0;
length = 0;
}
else
{
length = strlen(s);
str = new char[length + 1];
strcpy(str, s);
}
}

Calls to operator==() are converted into the awkward strcmp():

bool String::operator==(const String s) const
{
return (strcmp(str, s.str) == 0);
}

If s is an instance of String, then s[i] is translated to:

s.operator[](i)

We can take advantage of this fact and rewrite operator[] to perform index bounds checking. This is what makes smart strings smart:

char& String::operator[](int i)
{
if (i < 0 || length <= i)
error("index out of range");
return str[i];
}

Note that operator[] returns a reference to a char, hence can be called on the left side of an assignment operator:

// swap s[i] and s[j]
char temp = s[j];
s[j] = s[i];
s[i] = temp;

We redefine operator+() to perform string concatenation:

String operator+(const String& s1, const String& s2)
{
char* s = new char[s1.length + s2.length + 1];
strcpy(s, s1.str);
strcat(s, s2.str);
return String(s);
}

Functors

Allocators

An allocator encapsulates a heap and provides methods for allocating and deallocating items from the heap. Allocators are only needed if the system heap is unsatisfactory for a particular application. For example, a custom allocator might use a best-fit rather than a first-fit strategy, it may implement garbage collection, or it may compactify fragmented heaps. More commonly, allocators are used when a fixed size block of memory is frequently needed.

The allocator below maintains a list of free cells. A free cell is a union that can contain a cell or a pointer to the next free cell on the list. Complete details are given in a later chapter:

class Cell; // forward reference

class Allocator
{
public:
enum { NCELL = 100 };
Allocator(int n = NCELL);
union FreeCell { ... }; // Cell or FreeCell*
Cell* allocate(); // = next cell c on freelist, removes c
void deallocate(Cell* c); // puts c back on freelist
private:
FreeCell* freelist; // the actual heap
};

Cells are used to form trees and linked lists. We'll see a complete implementation of this later. Each cell contains a single data item, plus pointers to its logical neighbors. Here's how the sequence nums = ( 22 32 42 52 ) is represented as a doubly linked list of four cells:

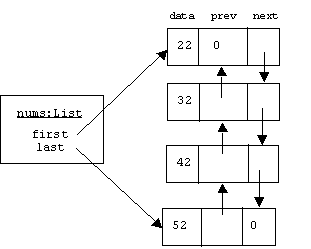
The data encapsulated by a cell is of type Item, where Item is defined by an easily changed typedef:

typedef int Item; // for now

The definition of Cell includes a static variable called myHeap of type Allocator*. Our definition takes advantage of the fact that a call to the new operator:

Cell* c = new Cell();

is translated into:

Cell* c = (Cell*)Cell::operator new(sizeof(Cell));

We redefine operator new() so that it calls myHeap->allocate(). sizeof() returns the number of bytes measured in size_t, which is defined in <stddef.h>. operator new() also returns a void*. Hence the prototype of our redefinition must be:

void* operator new(size_t bytes);

Calls to delete:

delete c;

are translated into:

Cell::operator delete((void*) c);

We can redefine operator delete() to call myHeap->deallocate©. The prototype must be:

void operator delete(void* p);

Here are the definitions:

class Cell
{
public:
void* operator new(size_t bytes)
{
if (bytes != sizeof(Cell))
throw logic_error("Wrong size!");
return myHeap->allocate();
}

void operator delete(void* p)
{
myHeap->deallocate((Cell*) p);
}

// etc.

private:
static Allocator* myHeap;
Item data;
Cell* next;
Cell* prev;
};

We must not forget to define myHeap:

Allocator* Cell::myHeap = new Allocator();

Supplying custom allocators is sometimes called the magic memory idiom, because calls to new don't appear to deplete the system heap.