Regular Labs

Regular Expressions

Lab 1A

Write regular expressions for the following languages. Test your solutions using String.matches.

Note: You can name a regular expression, then use the name in subsequent regular expressions, but you must avoid nested recursions.

For example:

Letter ::= [a-zA-Z]
Digit ::= [0-9]
Name ::= Letter~(Letter|Digit)*

The symbol "::=" is sometimes read "consists of".

It turns out that right-recursion is OK:

Word ::= Letter~Word?

But other forms of recursion are not OK.

a. L = all strings composed alternating blocks of 0s and 1s

b. L = all prices in dollars and cents. (e.g., $42.43)

c. L = all polynomials (e.g., 3x^2 + x – 5.6)

d. L = all finite sets of natural numbers (i.e., sequences of comma-separated numbers delimited by curly braces)

e. L = all possible URLs

f. L = all possible email addresses

g. L = all regular expressions in the form of quantified literals, unions of literals, and concatonations of literals, where a literal is any alpha-numeric string.

Lab 2

Implement an interpreter for simple arithmetic expressions. Here's a sample session:

-> 3.1 + 2.3
5.4
-> 3 * 6
18
-> 4.1 + pi
invalid number
-> 4.1 # 2.3
invalid operator
-> quit
Bye

Your interpreter should define a pattern for syntactically correct commands. The pattern is used to create a matcher for each command entered by the user. The matcher is used to extract the operator and arguments.

Lab 3

Implement and test a regular expressions language in Java. Use the following class diagram as your design:

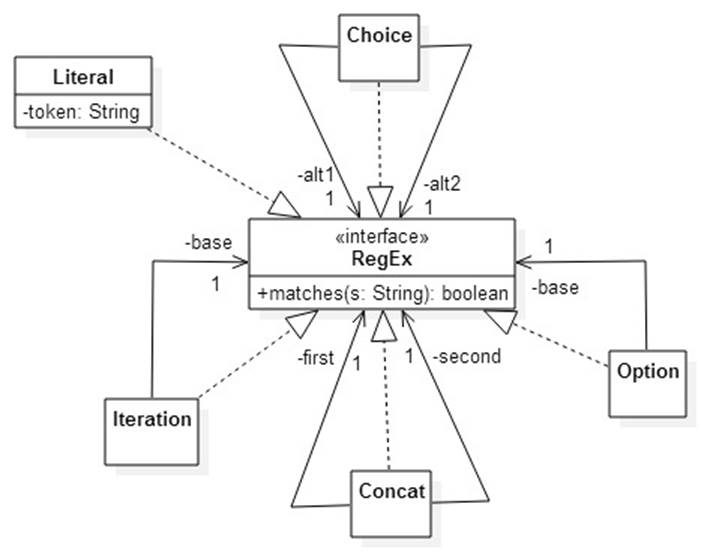
Lab 4 (Hard)

How would you implement

interface RegEx {
   public static RegEx compile(String regex) { ??? }
   // etc.
}

Finite State Machines

Lab 1B

Download and install StarUML 2.0.use the statechart diagramming feature to create statechart diagrams for finite state machines recognizing each of the languages below. (Transitions may be labeled by [else], [any], 0-9, a-z, a|b|c|d|e, etc. You may also assume that unspecified inputs cause self-transitions.)

a. L = L([0-9]*~(x|y|z)~(^~[0-9]+)?)

b. L = L((0|1)+~(\+|\*)~(0|1)+)

c. L = L((a+~b+)+~a*)

d. L = L((\(~ab~\))+)

e. L = L((sin | cos)~\(~[0-9]+(\.~[0-9]+)?~\))

Lab 5

Implement a FSM class in Java.

We can make a number of simplifying assumptions in the above definition of FSM:

M.STATES = int
M.start = 0
M.TOKENS = char

As a test, let's implement a FSM m that accepts all strings matching the regular expression 0⁺1⁺0⁺.

We begin by diagramming m:

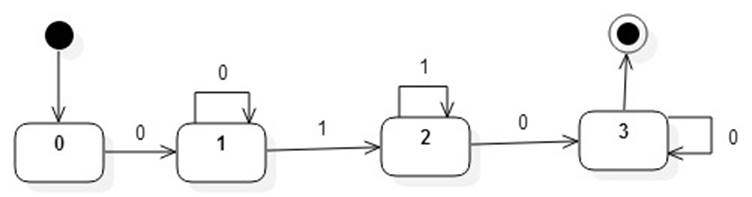
Notice that m.start = 0 and m.FINALS = {3}.

Here's a test that shows how m is built and used:

public static void test() {
      FSM m = new FSM();
      m.addTransition('0', 0, 1);
      m.addTransition('0', 1, 1);
      m.addTransition('1', 1, 2);
      m.addTransition('0', 2, 3);
      m.addTransition('1', 2, 2);
      m.addTransition('0', 3, 3);
      m.addFinalState(3);
     
      System.out.println("0011100: "+ m.accept("0011100"));
      System.out.println("01100: "+ m.accept("01100"));
      System.out.println("11100: "+ m.accept("11100"));
      System.out.println("001110011: "+ m.accept("001110011"));

      m.reset(); // clear all transitions and final states
     
   }

Here's the output:

0011100: true
01100: true
11100: false
001110011: false

Hints:

·       The transition method called by accept can simply consult a transitions table that associates configurations (current state + current token) with states (i.e., the next state). This approach guarantees that M.STATES will be finite.

·       We can save a lot of work by assuming unspecified inputs transition to an implicit dead state (dead = -1).

Lab 6

Use your FSM class to build FSMs that recognize strings matching the following regular expressions:

natRegEx = 0|[1-9][0-9]*

dateRegEx = [0-9][0-9]/[0-9][0-9]/[0-9][0-9]

nameRegEx = [a-c]([a-c]|[0-9])*

Lab 7

Add empty moves to FSMs by allowing users to add transitions triggered by the null char: \0. Modify your transition method so that it checks for both, a transition from the current token and state as well as a transition from the current state but replacing the current token with the null char.

Lab 8

Modify your FSM class so that FSMs are cloneable. (I.e., add a copy constructor or implement the Cloneable interface.)

Lab 9

Allow transitions to have guards. A guard is a boolean-valued lambda that expects the current configuration as input. The transition method executes the guard and only changes state if the result is true. (Of course the guard might be more powerful than an FSM.)

Lab 10

Enhance your FSM class by allowing states to be simple or composite:

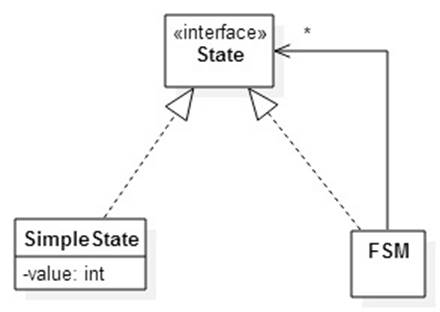
If the current state is an FSM, then its transition function is used to process tokens until it's final state is reached. At that point we resume using the transition of the parent or macro machine.

Lab 11

The FSM combiners class provides utility methods for combining FSMs to create new FSMs:

public class FSMCombiners {
  
   public static FSM append(FSM m1, FSM m2) {???}
   public static FSM union(FSM m1, FSM m2) {???}
   public static FSM iter(FSM m1) {???}
   public static FSM optional(FSM m1) {???}
   // etc?
}

Implement these methods. You may need to make further enhancements to the FSM classes.

The append method returns:

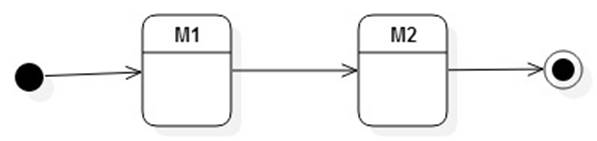
Hints (I think):

1.     Initialize the result by cloning M1.

2.     Add M2.transitions to the result, but add to each M2 state an offset greater than the largest state of M1. This will prevent confusion between M1 states and M2 states.

3.     Add an empty transition from each of M1's final states to M2's start state.

The union method returns:

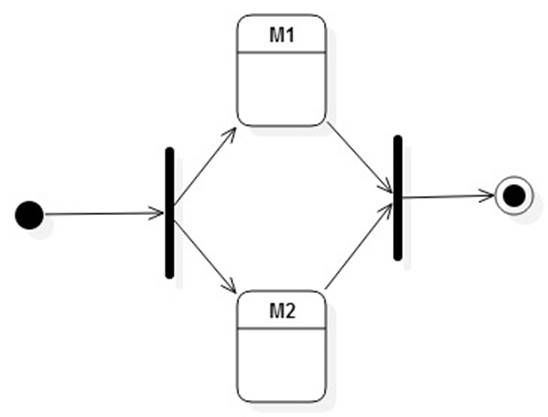
Hints:

Don't feel bad if you have to skip this one. Somehow the transition method needs to deal with the current state being pairs of ints instead of ints.

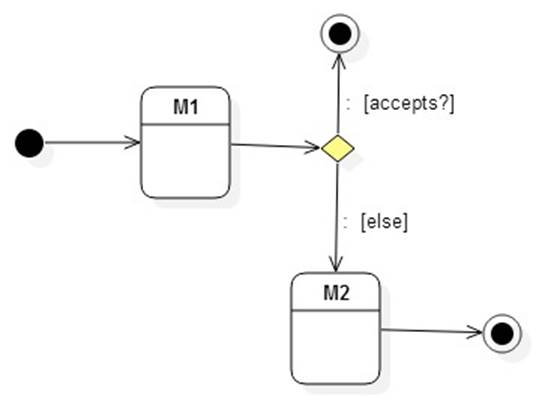
The iter method returns:

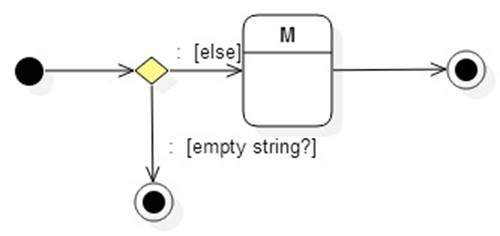
The optional method returns:

Lab 12 (Combinators)

We can think of an FSM as computing a function that takes a string as an input. If it matches or accepts a prefix of the input, then it outputs the remaining suffix. If the suffix is empty, then the input string was accepted.

Combinators allow us to combine such functions using the regular expression combiners.

Complete the implementation and test:

public class Combinators {
  
   public static UnaryOperator<String> seq(UnaryOperator<String> p1, UnaryOperator<String> p2) {
      return c->{
         String suffix = p1.apply(c);
         if (suffix.length() == c.length()) return suffix; // prefix not recognized
         else return p2.apply(suffix);
      };
   }
  
   public static UnaryOperator<String> alt(UnaryOperator<String> p1, UnaryOperator<String> p2) {???}
  
   public static UnaryOperator<String> rep(UnaryOperator<String> p) {???}
  
   public static UnaryOperator<String> opt(UnaryOperator<String> p) {???}
  
   public static UnaryOperator<String> prefix(String s) {???}
}

Regular Languages

Lab 13

Which of the following languages are in REG, prove your answers:

1. {0^k1^k | 1 <= k}

2. {0^k | k = 2*n for some n >= 1}

3. {0^k | k = 3*n + 2 for some n >= 1}

4. {0^k | k = n² for some n}

5. {0^p | p is prime}

6. Binary palindromes

7. All regular expressions