CFL Properties

Here's the big picture so far:

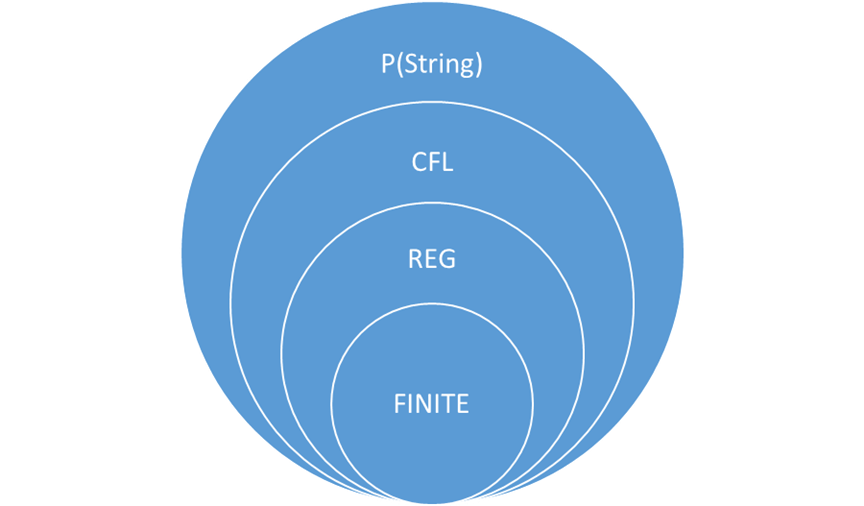
Theorem: REG is a proper sub-family of CFL

Proof: that REG is a subset of CFL should be clear since CFG patterns can be regular expressions.

To see that REG is a proper subset of CFL note that L = {0ⁿ10ⁿ | 0 < n} is not regular by the Pumping Lemma, but it's easy to find a CFG that generates L.

QED.

Theorem Assume L₁ and L₂ are CFLs, then so are L₁~L₂, L₁ U L₂, and L₁^*.

Proof: The idea is to combine the grammars for L₁ and L₂ to create grammars for L₁~L₂, L₁ U L₂, and L₁^*.

Theorem |CFL| = |NAT|

Proof

L is in CFL if L = L(G) for some CFG G. While there are infinitely many CFGs (why?), each CFG can be regarded as a string made from rules made from patterns made from characters. So |NAT| <= |CFL| <= |STRING| = |NAT|/

QED

Since we know |P(String)| > |String|, we know that there are many, many languages that are not CFLs. Are there any simple languages that are not CFLs?

Theorem { aⁱb^jc^k | i != j && j != k && i != k} is not a CFL.

Proof: This uses an analogue of the pumping lemma for CFLs called Ogden's Lemma.

Non-deterministic Push Down Automatas (NPDAs)

Recall that we showed

Theorem For every regular expression r, there is a finite state machine M such that L(r) = L(M), and vice-versa.

Here is the analogous theorem for CFLs:

Theorem For every CFG G where is a non-deterministic push-down automaton M such that L(G) = L(M), and vice-versa.

A push-down automaton (PDA) is basically a finite state machine with a stack:

PDA = FSM + statck

A non-deterministic PDA (NPDA) is like a quantum PDA which can be in multiple configurations simultaneously (each in a different parallel universe?) where a configuration is the state plus the contents of the stack:

configuration = state + stack

An NPDA accepts a string w if any of the parallel computations accepts w.

It's left as an exercise to build an emulator for NPDAs. It's not hard, but the resulting non-deterministic algorithm is very inefficient.