System Dynamics
The System Dynamics (SD) approach to modeling focuses on populations of agents rather than the agents themselves. For example, an SD model might monitor fluctuations in the population of all agents with income over a certain amount, who are infected by a certain virus, or who are unhappy with their government.
Stocks and Flows
A systems dynamics model consists of stocks and flows.
A stock is function that outputs the size of a population at a specific time: stock(t).
A flow measures the change of a stock over a period of time: flow(t).
Mathematically:
(stock(t + dt) - stock(t))/dt = flow(t)
Notice that as dt approaches 0, flow(t) approaches the derivative of stock(t).
References
http://en.wikipedia.org/wiki/Stock_and_flow
http://en.wikipedia.org/wiki/System_dynamics
Example: Exponential Growth
The earliest mathematical model of population growth was exponential growth: the growth rate is proportional to the population size.
Here's a stock and flow model of exponential growth:
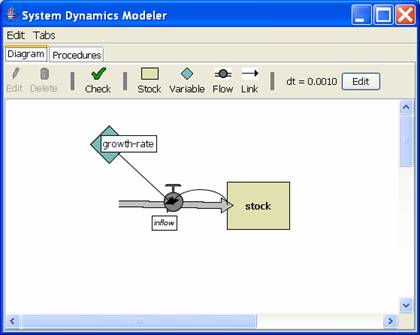
This model defines stock and inflow as follows:
stock(t + 1) = stock(t) + inflow(t)
inflow(t) = stock(t) * growth-rate
Equivalently:
stock(t + 1) = stock(t) * (1 + growth-rate)
In this case the inflow is the actual growth rate.
Solving for stock(t) gives the exponential function:
stock(t) = stock(0) * growth-ratet
For example, we can think of stock(t) is the size of a population of some organisms at time t and growth-rate is the rate of growth of the population.
Models
The Fifth Discipline Patterns
The Fifth Discipline is an interesting book that uses SD models to capture recurring problems in business.
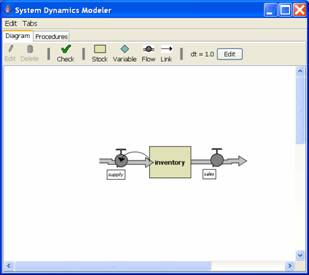
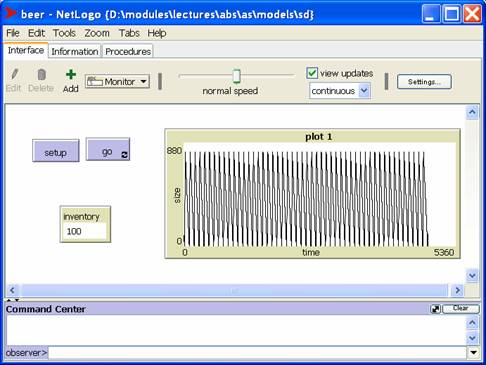
Balancing Process with Delay: The Beer Game
globals [
order-queue
]
to-report report-supply
let quantity 100 - inventory
ifelse quantity >= 0 [
set order-queue lput quantity
order-queue
]
[
set order-queue lput 0 order-queue
]
let shipment first order-queue
set order-queue butfirst order-queue
report shipment
end
Limits to Growth: The Logistics Equation
A more sophisticated model is the logistic map. In this model the carrying capacity of the environment exerts a negative pressure on the population size.
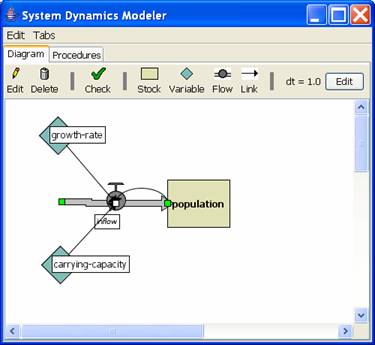
This model defines stock and inflow as follows:
population(t + 1) =
population(t) + inflow(t)
inflow(t) = growth-rate * population(t) * (1 – population(t) / carrying-capacity)
See my logistics model for the source.
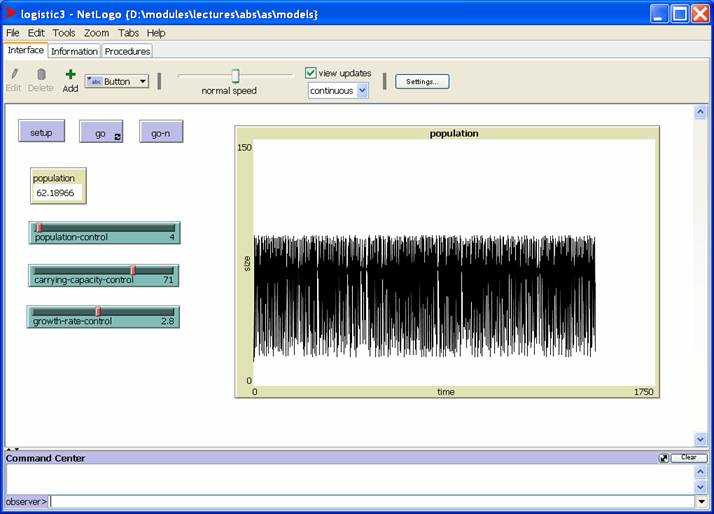
Here's a screen shot of the population in chaotic mode:
Shifting the Burden
Eroding Goals
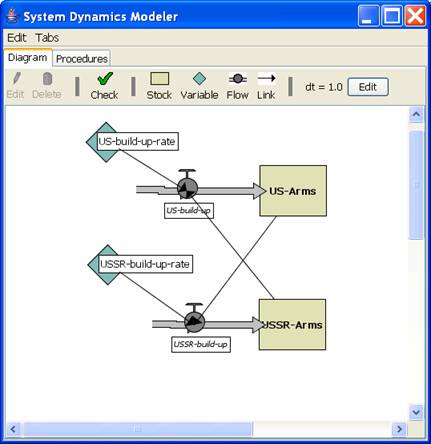
Escalation: The Arms Race