Cellular Automata

A cellular automata (CA) is a simple form of computer simulation that can be used to model systems that exhibit emergent behavior. Emergent behavior is when the behavior of the system is more complex or more interesting than the behavior of its components. For example, the brain can be thought of as a system that exhibits emergent behavior. Its components, neurons, have simple behavior: a neuron fires if enough of its neighbors fire. However, the brain exhibits very complex and interesting behavior: perception, attention, memory, speech, problem solving, emotions, etc.

A CA is a square grid of cells:

We can implement this using a two-dimensional array:

int size = 5;
Cell[] cells = new Cell[size][size];

So for example, we can refer to the cell in row i, column j as:

cell[i][j]

Each cell has a state:

cell[i][j].state

And 3 to 8 neighbors:

cell[i – 1][j – 1] // NW neighbor
cell[i – 1][j] // W neighbor
cell[i – 1][j + 1] // SW neighbor
cell[i][j - 1] // N neighbor
cell[i][j + 1] // S neighbor
cell[i + 1][j - 1] // NE neighbor
cell[i + 1][j] // E neighbor
cell[i + 1][j + 1] // SE neighbor

Updating a CA means updating each cell:

for(int row = 0; row < size; row++) {
for(int col = 0; col < size; col++) {
updateCell(row, col);
}
}

Updating a cell means computing a new state. The new state depends on the states of the neighbors:

cell[row][col].state = pollNeighborStates(row, col);

CA Component

We can implement a CA as a JComponent. The state of each cell is a color: red or blue:

class CAComponent extends JComponent {

private int size;
private Color[][] cells;
private Scanner kbd;

public CAComponent() {
kbd = new Scanner(System.in);
size = 50;
cells = new Color[size][size];
init(0.3);
}

The initialization method uses a random number generator to decide if a given cell should initially be red or blue:

private void init(double redProb) {
for(int row = 0; row < size; row++) {
for(int col = 0; col < size; col++) {
double rand = Math.random();
if (rand < redProb) {
cells[row][col] = Color.RED;
} else {
cells[row][col] = Color.BLUE;
}
}
}
}

The paintComponent method draws a red or blue fill square for each component:

public void paintComponent(Graphics gc) {
// get the height & width of the component:
int height = getHeight();
int width = getWidth();
int cellWidth = width/size;
int cellHeight = height/size;

for(int row = 0; row < size; row++) {
for(int col = 0; col < size; col++) {
gc.setColor(cells[row][col]);
gc.fillRect(row * cellWidth,
col * cellHeight,
cellWidth,
cellHeight);
}
}
}

An innovation of CAComponent is the inclusion of a CUI-style control loop that executes three user commands:

q = quit
u N = update CA N times
i P = reinitialize CA with red probability P

Here's the method:

public void controlLoop() {
while(true) {
System.out.print("-> ");
String token = kbd.next();
if (token.equals("q")) {
System.out.println("bye");
System.exit(1);
} else if (token.equals("u")) {
int n = kbd.nextInt();
updateCA(n);
repaint();
} else if (token.equals("i")) {
double p = kbd.nextDouble();
init(p);
repaint();
} else {
System.err.println("unrecognized command: " + token);
}
}
}

The call to repaint() generates a request to the OS to call paintComponent.

Updating the CA means updating each cell:

public void updateCA(int cycles) {
for(int cycle = 0; cycle < cycles; cycle++) {
for(int row = 0; row < size; row++) {
for(int col = 0; col < size; col++) {
updateCell(row, col);
}
}
}
}

The cell update method uses the majority rule: the color of a cell will be the color of the majority of its neighbors:

public void updateCell(int row, int col) {
int redCells = 0;
int blueCells = 0;
for(int i = row - 1; i <= row + 1; i++) {
for(int j = col - 1; j <= col + 1; j++) {
// ignore bad indices and current cell:
if (i < 0 || j < 0) continue;
if (size <= i || size <= j) continue;
if (i == row && j == col) continue;
// compute # of red & blue neighbors:
if (cells[i][j].equals(Color.RED)) {
redCells++;
} else { //if ((cells[i][j].equals(Color.BLUE)) {
blueCells++;
}
// change the color of current cell:
if (redCells < blueCells) {
cells[row][col] = Color.BLUE;
} else {
cells[row][col] = Color.RED;
}
}
}
}

} // end of class CAComponent

CA Viewer

We need a viewer:

public class CAViewer {

public static final int FRAME_WIDTH = 300;
public static final int FRAME_HEIGHT = 400;

public static void main(String[] args) {
JFrame frame = new JFrame();
frame.setSize(FRAME_WIDTH, FRAME_HEIGHT);
frame.setTitle("Frame Viewer");
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
// create custom component:
CAComponent component = new CAComponent();
frame.add(component);
frame.setVisible(true);
// start control loop:
component.controlLoop();
}
}

Note the last line starts the CUI control loop.

Example: Simulating Voting Patterns

Ever wonder why there are red (Republican) states and blue (Democratic) states? Why shouldn't Republicans and Democrats be evenly distributed throughout the country? Ever notice how your political opinions are influenced by the political opinions of your neighbors?

We can use a CA to suggest an answer. Here's a map showing a random distribution of Republican counties and Democratic counties. In this map the probability of being a Republican is set to 0.3:

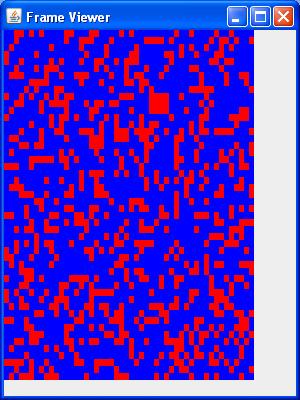
Here is the map after the command "u 10", which updates the CA 10 times. At this point the map is stable. In other words it doesn't change with further updates. Note how the Republicans have coalesced into four red states surrounded by an ocean of blue states:

Let's restart the simulation by giving the command "i .35". In other words, the probability of being a Republican is 0.35. Here's the new map:

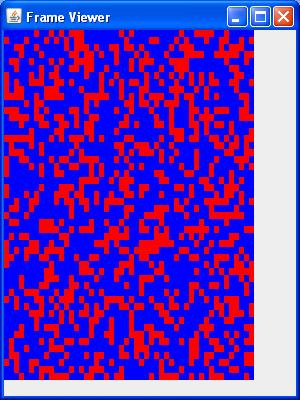
Next we update 50 times: "u 50". Here's the map:

Note the stable enclave of Republicans in the south. After 10 more updates the republicans will take over the north.

Notes

The update rule can be modified in various ways. Also, the number of parties (colors) can be increased.

Note that red and blue don't have to represent political affiliations; they can also represent cultural traits, for example.