Type Theory

Errors

Definitions

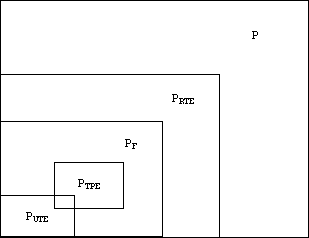
P = All (syntactically correct) phrases of language L.
P_RTE = All phrases containing runtime errors.
P_UTE = All phrases containing untrapped runtime errors.
P_F = All phrases forbidden by the language processor.
P_TPE = All phrases containing type errors.

Here are the relationships between these classes:

Examples of runtime errors:

Divide by 0 (trapped but not forbidden)
Null pointer reference (untrapped)
Message not understood (type error)
Array index out of bounds (untrapped in C)
Undefined symbol (forbidden)
Argument has wrong type (type error)
Illegal user command (trapped but not forbidden)
Illegal cast (type error)

More Definitions

L is strongly checked or safe if untrapped errors are forbidden.
L is type safe if type errors are forbidden.
L is statically type safe if type errors are forbidden at compile time.

Type Systems

A type consists of a domain and a set of operations:

type = <domain, operations>

A type system consists of:

1. a set of primitive types
2. a set of type constructors
3. a subtype partial ordering: T1 <: T2
4. an equivalence relationship T1= T2
5. Rules and axioms for type checking

Example

A type system might consists of primitive types Boolean, char, integer, and float. The type constructors map, product, and array. The compatibility relationship obeys the rules:

T[] = all arrays of type T values
T1 x ... x Tn = all n-tuples of the form (v1, ..., vn) where vi: Ti
T1->T2 = all functions with domain = T1 and range = T2

There are two types of equivalence relationships: literal equality or structural equality.

Example: The Java Type System

The primitive types of Java are:

boolean, char, byte, short, int, long, float, and double

here are the subtype relationships between them:

char <: int
byte <: short <: int <: long <: float <: double
float <: double

The reference types of Java are array types, interface types, and class types.

If T is a type then so is T[]

If IV is a list of instance variable definitions and M is a list of method definitions, then

interface {M} and class {IV; M} are types

here are some rules governing reference subtypes:

Let C, Ci denote a class type, I, Ii denote an interface type, R, Ri denote an reference type.

C1 <: C2 if C1 extends C2
I1 <: I2 if I1 extends I2
C <: I if C <: C' & I <: I' & C' implements I'
R1[] <: R2[] if R1 <: R2
R <: Object

Primitive types are not subtypes of reference types and vice-versa

!R <: P & !P <: R

Axioms and Rules

In the following we will assume symbols beginning with a lower case letter represent phrases and symbols beginning with an upper case letter represent type expressions.

A judgment has the form:

CTX |- p:T

This is read:

Context CTX entails that phrase p has type T

where E is a type expression.

A rule has the form:

CTX |- p₁:T₁ CTX |- p_n:T_n
CTX |- p:T

This is read:

if context CTX entails p₁:T₁ ... p_n:T_n, then we can infer that CTX entails p:T.

Staring with axiomatic judgments we can build derivation trees. Each node of such a tree is a judgment. The parents of a node are given by a rule. The root of a derivation tree is a theorem.

A type system is sound if

CTX |- e:E implies e.exec(CTX) is an instance of E.exec(CTX)

where e is a phrase and E is a type expression.

Of course we also want decidability:

CTX |- e:E implies e.typeOf(CTX) = E.exec(CTX)

Expressions

For each type constructor there are usually four rules. The formation rule tells us how to build the new type, the elimination rule tells us how to break it down, the introduction rule tells us how to build new phrases of the new type, and the computation rule tells us how to break down these new phrases.

Rules for map

In this section we will represent the type expression (map A B) as A->B.

Formation Rule

CTX |- A:Type CTX |- B:Type
CTX |- (A->B):Type

Elimination Rule

CTX |- f: A->B CTX |- a:A
CTX |- (f a): B

Introduction Rule

CTX + x:A |- b:B
CTX |- (function ((x A)) b): A->B

Computation Axiom

CTX + f=(function ((x A) b) |- c: A
CTX + f=(function ((x A) b) + x=c |- (f c) => b

In other words, the function call (f c) reduces to (=>) the body, b, in a context extended by the binding x=c.

The Curry-Howard Isomorphism

Remarkably, there is a close correspondence between type theory and constructive logic. We only need to reinterpret p:T to mean "p is a proof of formula T".

Of course we need to reinterpret the type constructors:

map = implication
product = conjunction
disjoint union = disjunction

Rules for -> (implication)

Formation Rule

Assume WFF = all well-formed formulae, then:

CTX |- A:WFF CTX |- B:WFF
CTX |- (A->B):WFF

Elimination Rule

In constructive logic A->B means there is a function that transforms proofs of A into proofs of B:

CTX |- f: A->B CTX |- a:A
CTX |- (f a): B

Introduction Rule

If from an arbitrary proof x of A we can build a proof b of B, then we have a function that transforms proofs of A into proofs of B, hence a proof of A->B:

CTX + x:A |- b:B
CTX |- (function ((x A)) b): A->B

Computation Axiom

Given a proof of A, we only need to plug it into our function to get a proof of B:

CTX + f=(function ((x A) b) |- c: A
CTX + f=(function ((x A) b) + x=c |- (f c) => b

Commands

Assume commands return the token "done" if they are executed correctly. Assume this token is the only instance of type Cmmd:

Formation Axiom

CTX |- Cmmd:Type

Introduction Axioms and Rules

CTX |- done:Cmmd

CTX |- x:var<A> CTX |- a:A
CTX |- {assign x a}: Cmmd

CTX |- e:Boolean CTX |- a:Cmmd
CTX |- {while e a}: Cmmd

CTX |- e:Boolean CTX |- a:Cmmd CTX |- b:Cmmd
CTX |- {if e a b}: Cmmd

etc.

Elimination Rules

Computation Rules

CTX |- e => true CTX |- {if e a b}: Cmmd
CTX |- {if e a b} => a

CTX |- {assign x a}: Cmmd
CTX |- {assign x a} => CTX + *x=a

etc.

Definitions

Assume the result of executing a definition is the token "ok". Assume that this token is the only instance of the type Def.

Formation Axiom

CTX |- Def:Type

Introduction Axioms & Rules

CTX |- ok:Def

CTX |- A:Type CTX |- e:A
CTX |- [define x A e]: Def

Computation Rule

CTX |- e:A
CTX |- [define x A e] => CTX + x:A + x=e

This rule states:

If CTX entails that expression e has type A, then CTX entails that executing the declaration [define x A e] adds the binding x:A to CTX.

Subtyping and Type Equivalence

Let A<:B denote that A is a subtype of B. let A=B denote that A and B are equivalent.

CTX |- A<:A

CTX |- A<:B CTX |- B<:C
CTX |- A<:C

CTX |- a:A CTX |- A<:B
CTX |- a:B

CTX |- A=A

CTX |- A=B CTX |- B=C
CTX |- A=C

CTX |- A=B
CTX |- A<:B

CTX |- A<:B CTX |- B<:A
CTX |- A=B

At this point we could introduce rules that show the interplay between <: and type constructors. For example:

CTX |- A'<:A CTX |- B<:B'
CTX |- (A->B)<:(A'->B')

CTX |- A=B
CTX |- var<A>=var<B>

etc.