Theta 1.0

Theta Syntax

A phrase is a basic unit of executable syntax. There are three families of phrases:

Each family represents a different notion of execution. Executing a declaration adds a binding to an environment. Executing an expression produces a value. Executing a command updates a variable. Commands will appear in a subsequent version of Theta.

Theta Declarations

Executing a Theta declaration binds a new symbol to a type and initial value:

<Declaration> ::= [define <Symbol> <Expression> <Expression>]

For example:

-> [define pi Number 3.14]
ok
-> [define flag Boolean false]
ok
-> [define oops Boolean 0]
Error: type mismatch!

Theta Expressions

There are four types of Theta expressions:

Literals include numerals, true, and false:

<Literal> ::= <Numeral> | true | false

A symbol (also called a name or identifier) is a sequence of alphanumeric characters beginning with a letter.

As in Lisp, a function call is simply a list of one or more expressions delimited by parentheses:

<FunCall> ::= (<Expression>+)

The value of the first expression in the list, called the operator, is a function. The values of the subsequent expressions (called operands) are the arguments to be passed to the function. The value produced is the return value of the function.

Special forms will be introduced in a subsequent version of Theta.

Executing a Theta expression produces a value. Theta values include numbers, Booleans, functions, types, objects, and classes. For example:

-> (+ 2 (* 2 2)) // fun call
6
-> 42.7 // literal
42.7
-> pi // symbol
3.14
-> (and false (< 3 4)) // fun call
false

The Theta Interpreter

We can specify the semantics of Theta (i.e., what behavior should occur when a phrase is executed) by building an interpreter for Theta. This is called operational semantics or semantic prototyping. Our interpreter is implemented in Java. We say that Theta is the object language while Java is the meta language.

Our Theta interpreter customizes the CUI framework and uses the Lex utilities. These come from the jutil package, which can be found at:

http://www.mathcs.sjsu.edu/faculty/pearce/jutil/

Here is the complete code:

import jutil.*;
import java.util.*;

public class ThetaConsole extends Console {

   private String regExp = null;

   public ThetaConsole(Context ctx) {
      super(ctx);
      regExp = Lex.NUMBER;
      regExp = Lex.join(regExp, Lex.SYMBOL);
      regExp = Lex.join(regExp, Lex.OPERATOR);
      regExp = Lex.join(regExp, Lex.PUNCTUATION);
   }

   public ThetaConsole() { this(new Context()); }

   public String execute(String cmmd) throws AppError {
      List tokens = Lex.scan(regExp, cmmd);
      Phrase phrase = Phrase.parse(tokens);
      Type type = phrase.type((Context)model);
      if (type.equals(Type.ERROR))
         throw new AppError("type mismatch!");
      System.out.println("type = " + type);
      Object value = phrase.exec((Context)model);
      return value.toString();
   }

   public static void main(String[] args) {
      ThetaConsole console = new ThetaConsole();
      console.controlLoop();
   }
}

Parsing Theta Phrases

The Theta interpreter uses the Lex utility to scan the phrase entered by the user into a list of tokens. A simple parser converts the list of tokens into an internal tree-like representation of the phrase. We use a hierarchy of classes to represent different types of phrases:

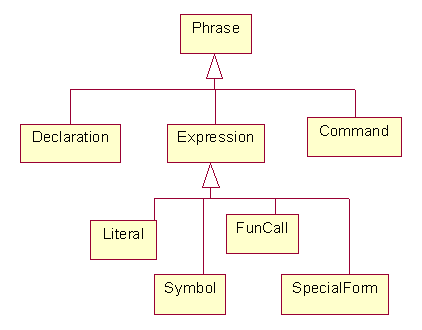
Here's a sketch of the Phrase base class:

abstract public class Phrase {
   public static Phrase parse(List tokens) throws AppError {
      if (Expression.isNext(tokens)) return Expression.parse(tokens);
      if (Command.isNext(tokens)) return Command.parse(tokens);
      if (Declaration.isNext(tokens))
         return Declaration.parse(tokens);
      throw new AppError("Unrecognized phrase");
   }
   public Type type(Context ctx) throws AppError {
      return Type.VOID; // redefine in Expression subclasses
   }
   abstract public Object exec(Context ctx) throws AppError;
}

The Theta Type System

Theta types such as number and Boolean are regarded as ordinary values no different than 3.14 or true. Types are represented by instances of a Java class called Type or of one of its subclasses:

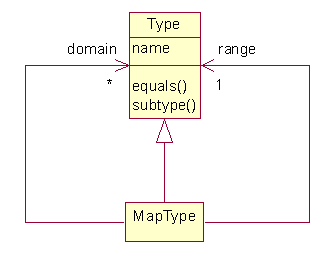
Theta primitive types include Boolean, Error, Number, Void, and Type. Theta composite types include map, the type of all functions. For example, the type of the greaterThan function (>) would be:

(map Number Number Boolean)

Note that Boolean represents the range of greaterThan. The other types represent the domain. We might write this using Mathematical notation as:

Number x Number -> Boolean

Here's a sketch of the declaration of the Type class:

public class Type {
   public static Type BOOLEAN = new Type("Boolean");
   public static Type ERROR = new Type("Error");
   public static Type NUMBER = new Type("Number");
   public static Type TYPE = new Type("Type");
   public static Type VOID = new Type("Void");
   private String name;
   public Type(String name) { this.name = name; }
   public Type() { this("unknown"); }
   public String toString() { return name; }
   public String getName() { return name; }
   public boolean equals(Object other) {
      // ???
   }
   public boolean subtype(Type t) { return false; }
   // etc.
}

A type expression is simply an expression that has a type as its value. For example, we may regard "Number" as a symbol of type Type.Type and value Type.Number. We may regard (map Number Number Boolean) as a call to the map function that produces an instance of MapType as its value.

Note:

What is the type of the map operator? The domain is a list of types and the range is a type, so it would be something like this:

(map Type Type ... Type)

Of course the ... doesn't make any sense. To fix this problem we need to add another type constructor to our type system. This will be the list constructor. So now we can say that the type of map is:

(map (list Type) Type)

Of course you will need to add a new primitive operator, list, to the system, and a new class of values:

class ListType extends Type {
Type elemType;
// etc.
}

With this type we can allow the + and * operators to be of type:

(map (List Number) Number)

Type Checking

The purpose of types is to catch errors before execution. This goal often presents a tradeoff between safety and flexibility.

The Theta Context

The Theta context is the execution environment for all Theta phrases.

The Theta context includes a table containing bindings of names to their types and values. This table is called the environment. It might be represented as a map that associates strings to type-value pairs:

map<String, TypeValuePair> environment;

Initially, the environment should contain bindings of the names of primitive functions (+, *, -, /, <, >, =, and, or, not) and primitive types (Number, Boolean, Type, Errror) to their respective types and values.

Problem

Complete the implementation of version 1.0 of the Theta interpreter.