Design Metrics

Basic Sets

In this section we introduce a simple notational scheme for defining sets of components of a system:

packages(S) =
the set of packages declared in S (including subpackages)

classes(S) =
the set of classes declared in S (including inner classes)

methods(S) =
the set of methods declared in S

Of course these sets can be defined and refined for the components of S:

methods(C) =
the set of methods declared or inherted by class C
attributes(C) =
the set of attributes declared or inherted by class C
declaredMethods(C) =
the set of methods declared by class C
declaredAttributes(C) =
the set of attributes (i.e., fields) declared by class C

Here are some important sets that relate to the dependency graph of a system:

clients(N) = {M | M ref N}
dependents(N) = {M | M dep N} = TC(clients(N))
providers(N)= suppliers(N) = {M | N ref M}
dependencies(N) = {M | N dep M} = TC(providers(N))

Notation:

if X is a set, let #X = the cardinality (i.e., size) of X

Assume X is a set of numbers, then:

sum(X) = sum of all members of X
average(X) = sum(X)/#X
max(X) = the largest element in X
etc.

Basic Metrics

The basic metrics are simply the cardinalities of the basic sets:

NP(S) = #packages(S)
NC(S) = #classes(S)
NM(S) = #methods(S)
NR(S) = #references(S)

We can refine some of these metrics:

NAC(S) = #abstractClasses(S) // includes interfaces

We can extend some of these metrics to the components of S:

NC(P) = #classes(P) // P = some package of S
NM(C) = #methods(C) // S = some class of S
etc.

Some of these extended metrics can be refined, too. For example:

NDM(C) = #declaredMethods(C)

The encumbrance of a component roughly measures its reusability and portability:

encumbrance(N) = #dependencies(N)

The Chidamber & Kemerer (CK) Suite

Download a tool that implements the CK suite from:

http://www.spinellis.gr/sw/ckjm/

Weighted Methods per Class (WMC)

Assume C is a class in system S:

WMC(C) = sum(complexity(m)) for m in declaredMethods(C)
WMC(S) = average(WMC(C)) for C in classes(S)
complexity(m) = 1 or cyclomaticComplexity(m)

Cyclomatic Complexity (CC)

Assume m is in declaredMetods(C). Let control (m) be the control flow graph of a function. This is a directed graph in which nodes are statements and an arrow connecting node s1 to node s2 indicates that s2 might be executed immediately after s1. In essence, control(m) is a flow chart.

e = # edges in control(m)
n = # nodes in control(m)
d = # decision nodes in control(m) =
# nodes with multiple exiting arrows
cyclomaticComplexity(m) = e - n + 2 = # paths = d + 1

Note: From graph theory we have Euler's theorem:

f - e + n = 2

where

f = # faces in a graph G

A face is a region in the plane bounded by edges of a graph. Clearly the boundary of the face represents two paths in the graph.

We can get a good estimate of cyclomaticComplexity(m) by counting the number of branching statements that occur in the body of m. These include:

if, else, while, for, do, case

Depth of Inheritance Tree (DIT)

The more classes a class C inherits from, the more complex it becomes. In general, tall inheritance hierarchies are less desirable than short ones.

Assume C and B are classes:

DIT(C) = max (1 + DIT(B)) where C is in extensions(B)
DIT(S) = average(DIT(C)) for C in classes(S)

Number of Children (NOC)

While DIT measures the depth of an inheritance hierarchy, NOC measures its width. If class C has many children, then a small change in C can have a big impact. C must be tested more exhaustively than other classes. Ideally, if NOC(C) is large, then DIT(C) should be small since this increases the reusability of C.

Assume C is a class:

NOC(C) = #extensions(C)
NOC(S) = average(NOC(C)) for C in classes(S)

Coupling Between Objects (CBO)

We have already discussed the desirability of a low coupling degree. C&K simply take coupling degree of class C to be the number of references it contains to other classes. (Note: C&K use the phrase "A is coupled to B" the same way I use the term "A references B".)

Recall

Ce(N) = the set of efferent coulings of N

CBO(C) = #Ce(C)
CBO(S) = average(CBO(C)) for C in classes(S)

Response for a Class (RFC)

RFC measures the number of methods that might be involved when an object receives a message. A large value of RFC indicates a more complex class with a large set of dependencies. Such a class can be difficult to understand and maintain.

Assume m is in DeclaredMethods(C).

Calls(m) = all methods called by m
CallGraph(m) = transitive closure of Calls(m)

RFC(m) = #Calls(m) or #CallGraph(m)
RFC(C) = max RFC(m) for m in DeclaredMethods(C)
RFC = average RFC(C) for all C

Lack of Cohesion for Methods (LCOM)

The methods of a cohesive class work together to achieve a common goal. Classes that try to do too many marginally related tasks are difficult to understand, reuse, and maintain.

Although there is no precise way to measure the cohesiveness of a class, we can identify several common "degrees" of cohesiveness. At the low end of our spectrum is coincidental cohesion. A class exhibits coincidental cohesion if the tasks its methods perform are totally unrelated:

class MyFuns {
void initPrinter() { ... }
double calcInterest() { ... }
Date getDate() { ... }
}

The next step up from coincidental cohesion is logical cohesion. A class exhibits logical cohesion if the tasks its methods perform are conceptually related. For example, the methods of the following class are related by the mathematical concept of area:

class AreaFuns {
double circleArea() { ... }
double rectangleArea() { ... }
double triangleArea() { ... }
}

A logically cohesive class also exhibits temporal cohesion if the tasks its methods perform are invoked at or near the same time. For example, the methods of the following class are related by the device initialization concept, and they are all invoked at system boot time:

class InitFuns {
void initDisk() { ... }
void initPrinter() { ... }
void initMonitor() { ... }
}

One reason why coincidental, logical, and temporal cohesion are at the low end of our cohesion scale is because instances of such classes are unrelated to objects in the application domain. For example, suppose x and y are instances of the InitFuns class:

InitFuns x = InitFuns(), y = new InitFuns();

How can we interpret x, and y? What do they represent? How are they different?

A class exhibits procedural cohesion, the next step up in our cohesion scale, if the tasks its methods perform are steps in the same application domain process. For example, if the application domain is a kitchen, then cake making is an important application domain process. Each cake we bake is the product of an instance of a MakeCake class:

class MakeCake {
void addIngredients() { ... }
void mix() { ... }
void bake() { ... }
}

A class exhibits informational cohesion if the tasks its methods perform are services performed by application domain objects. Our Airplane class exhibits informational cohesion, because different instances represent different airplanes:

class Airplane {
void takeoff() { ... }
void fly() { ... }
void land() { ... }
}

Note that the informational cohesion of this class is ruined if we add a method for computing taxes or browsing web pages.

C&K measure the inverse of cohesion called lack of cohesion. There are several variants of this metric (LCOM2, LCOM3) that improve on the original LCOM1:

LCOM1

A class C can be represented as a weighted undirected graph G(C) = <N, E>. N, the nodes of G(C), are the declared methods of C. An edge in E connects two methods if those methods reference a common attribute of C. The weight of an edge is the number of common fields referenced.

LCOM1(C) = max(0, #(N x N) - 2 * #E)

In other words, LCOM1(C) is the number of pairs of methods that don't share attributes minus the number of pairs of methods that do share attributes.

A low value of LCOM1(C) indicates a high degree of coupling between the methods of C, hence we can suppose C has a high degree of cohesion.

LCOM2 and LCOM3

LCOM2 is an improved version of LCOM1.

m = #declaredMethods(C)
a = #declaredAttributes(C)
m(A) = # of methods in C that reference attribute A
s = sum(m(A)) for A in declaredAttributes(C)
LCOM2(C) = 1 - s/(m * a)

LCOM3 is another improvement:

LCOM3(C) = (m - s/a)/(m - 1)

Note:

0 <= LCOM3(C) <= 2

If LCOM3(C) > 1, then C should probably be refactored into two classes.

Stability and Independence (from Martin's paper)

Let K be a collaboration (category). This is a collection of classes that 1) change together if ever, 2) Reused together, 3) Have a common goal. Design patterns are recurring collaborations.

Ca(K) = #classes outside of K that depend on classes in K
Ce(K) = #classes in K that depend on classes outside of K
instability(K) = Ce(K)/(Ca(K) + Ce(K))

A collaboration K is responsible if Ca(K) is large. K is independent if Ce(K) is small.

Note that:

0 <= instability(K) <= 1

K is stable if instability(K) is close to 0. In this case K has few dependencies on other classes. These classes can change without affecting K. Also, K is responsible since more classes depend on K rather than the other way around.

If instability(K) is close to 1, then most of the references are efferent. Changes to classes outside of K may affect K.

We can have our cake and eat it to. The behavior of K can be changed without changing the members of K if K contains a lot of abstract classes:

abstractness(K) = #abstract classes in K/# classes in K

Note:

0 <= abstractness(K) <= 1

For every collaboration K we can plot its abstraction and instability:

(instability(K), abstractness(K)) = (A, I)

K is well balanced if instability and abstractness are close. We can measure this by measuring the distance from the point (A, I) to the line a + i = 1. This line is called the main sequence (a graph in astronomy that plots the size and brightness of stars):

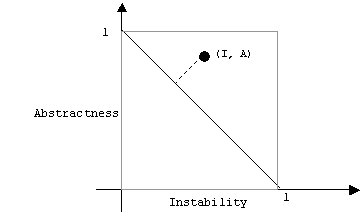
The distance from (I, A) to the main sequence is given by the formula:

dist(K) = |(A + I - 1)/2|

This should be close to 0.

Metrics for Object-Oriented Design (MOOD)

Method Hiding Factor (MHF)

Let m be in methods(S):

invisibility(m) = #classes(S) where m is invisible/#classes(S)
MHF(S) = sum(#invisibility(m)) for m in methods(S)/#methods(S)

Attribute Hiding Factor (AHF)

Let a be in attributes(S):

invisibility(a) = #classes(S) where a is invisible/#classes(S)
AHF(S) = sum(#invisibility(a)) for a in attributes(S)/#attributes(S)

Method Inheritance Factor (MIF)

inheritedMethods(C) = all methods inherited by C
MIF(C) = #inheritedMethods(C)/#methods(C)
MIF(S) = avg(MIF(C)) for C in classes(S)

Attribute Inheritance Factor (AIF)

inheritedAttributes(C) = all attributes inherited by C
AIF(C) = #inheritedAttributes(C)/#attributes(C)
AIF(S) = avg(AIF(C)) for C in classes(S)

Polymorphism Factor (PF)

This is the number of overridden methods divided by the number of possible overrides.

PF(S) = # of overides/sum(#methods(C) * #subclasses(C))

Coupling Factor (CF)

#(classes(S) x classes(S))/#associations(S)