Artificial Life

Here's a good definition of A-Life that I found on the web (but couldn't find where it came from):

"A-life" attempts to model biological processes and phenomena on computers. Some main themes in a-life are emergence and adaptation. Emergence is when behavior on a group level transcends the simpler actions of its individuals, and adaptation is when individuals or groups respond to changes in an environment. Of particular interest to a-life researchers is adaptation through evolution. Complexity research, particularly at the Santa Fe Institute, is closely allied to a-life.

A popular A-life model is the cellular automaton (CA). Here's a definition of CA from Wikipedia:

It (a CA) consists of an infinite, regular grid of cells, each in one of a finite number of states. The grid can be in any finite number of dimensions. Time is also discrete, and the state of a cell at time t is a function of the state of a finite number of cells called the neighborhood at time t-1. These neighbors are a selection of cells relative to some specified, and does not change (Though the cell itself may be in its neighborhood, it is not usually considered a neighbor). Every cell has the same rule for updating, based on the values in this neighbourhood. Each time the rules are applied to the whole grid a new generation is produced.

Conway's Game of Life was an interesting early example of a CA.

Clearly the cells of finite, two-dimensional CAs can be represented by NetLogo patches.

References

http://www.math.com/students/wonders/life/life.html

http://www.alife.org/

http://www.alcyone.com/max/links/alife.html

http://en.wikipedia.org/wiki/Artificial_Life

A simple voting model

Ever wonder about the blue state/red state phenomenon? Why aren't republicans and democrats more evenly distributed? The simplest example of emergence occurs when the state of an (stationary) agent is determined by the states of his neighbors. It's surprising that this sort of provincial behavior can generate global behavior patterns.

Screen Shots

Red patches represent republican counties, blue patches represent democratic counties, and green patches represent counties of undecided or unaligned voters.

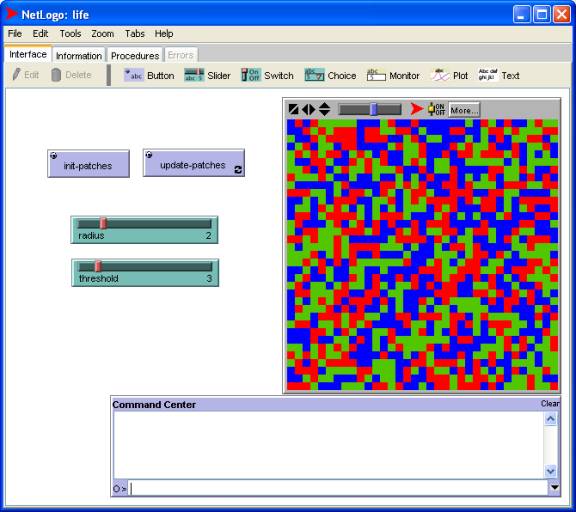
Before

We are using the rule that a county will become republican (democrat) if at least N counties within an M-county radius are republican (democrat), while the number of democratic (republican) counties is less than N.

Initially, we assume the distribution of republican, democratic, and undecided counties is random. In the run below N = threshold = 3 and M = radius = 2.

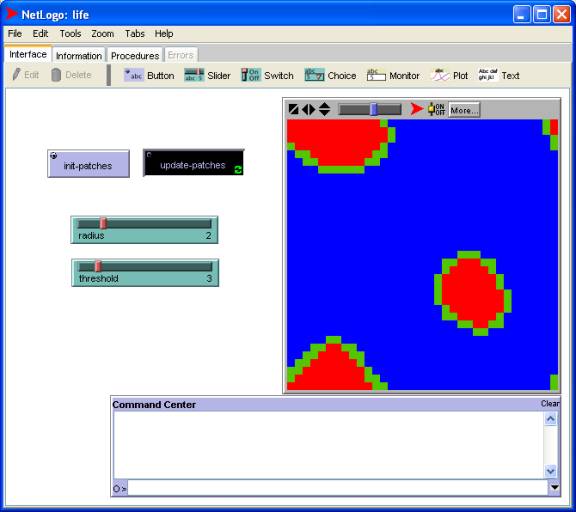
After

After several cycles we notice islands of republicans buffered from oceans of democrats by beaches of undecided voters:

Procedures

Initializing patches

to init-patches
ca
ask patches [init-patch]
end

to init-patch
locals [i]
set i random 3
ifelse i = 0
[set pcolor red]
[ifelse i = 1
[set pcolor blue]
[set pcolor green]]
end

Updating patches

to update-patches
ask patches [update-patch]
end

We use the "with" operator combined with the in-radius operator:

agent-set in-radius R with [property = p]

This generates the set of all agents within radius R of any agent in agent-set. We filter all agents from this set that don't satisfy property = p.

to update-patch
locals [republicans democrats undecided]
set republicans count
(patches in-radius radius with [pcolor = red])
set democrats count
(patches in-radius radius with [pcolor = blue])
set undecided count
(patches in-radius radius with [pcolor = green])
ifelse (republicans > threshold) and (democrats < threshold)
[set pcolor red]
[ifelse (democrats > threshold and republicans < threshold)
[set pcolor blue]
[set pcolor green]]
end

The GUI

The GUI consists of buttons associated with the init-patches and update-patches procedures. The second button is a forever button. Sliders set the global variables threshold and radius.