Epsilon

Epsilon extends Delta by adding user-defined functions and procedures.

Syntax

Epsilon programmers create functions and procedures using expression and command abstractions, respectively:

<SpecialForm> ::= <ExpAbstraction> | <CmmdAbstraction> | etc.

More specifically, a function is created from an expression (called the body or implementation) and a list of parameters by using the fun operator. A procedure is created from a command (also called the body or implementation) and a list of parameters by using the proc operator:

<ExpAbstraction> ::= (fun (<Symbol>*) <Expression>)
<CmmdAbstraction> ::= (proc (<Symbol>*) <Command>)

A procedure call is a new type of command:

<Command> ::= <ProcCall> | etc.

In Epsilon a function call is simply a list of one or more expressions surrounded by parenthesis, while a procedure call is a list of one or more expressions surrounded by curly braces:

<ProcCall> ::= {<Expression>+}
<FunCall> ::= (<Expression>+)

The first expression in the list is the operator (this is usually just a symbol). The subsequent expressions are the operands.

Demonstration

Here's how an Epsilon programmer defines a variable, a function, and a procedure:

-> [define w (var 10)]
done
-> [define square (fun (x) (* x x))]
done
-> [define incW (proc (y) {assign w (+ (val w) y)})]
done
-> w
var<10>
-> square
<function>
-> incW
<procedure>

Now lets call square and incW:

-> (square (val w))
100
-> {incW 2}
ok
-> w
var<12>

Of course calls can be nested:

-> {incW (square (+ 2 3))}
ok
-> w
var<37>

Epsilon permits anonymous function and procedure calls:

-> ((fun (x) (* 2 x)) 3)
6

Functions (and procedures) can be the return values of other functions:

-> [define incX (fun (x) (fun (y) (+ x y)))]
done
-> [define inc3 (incX 3)]
done
-> inc3
<function>
-> (inc3 7)
10

Epsilon employs the static scope rule. This means that the values of non-locals (i.e., symbols appearing in the body that are neither parameters nor symbols defined in a nested block) are determined by the function's defining environment, not its calling environment. Consider the following example:

-> [define a 100]
done
-> [deine addA
(let [[define a 50] [define b 30]] (fun (c) (+ a b c)))]
done
-> (let [[define b 500]] (addA 20))
100

The body of the addA function contains four symbols: +, a, b, and c. In the environment in which addA is defined a = 50, b = 30, + = the primitive add function, and c is a parameter. However, in the environment in which addA is called a = 100 and b = 500. Nevertheless, the value returned is (+ 50 30 20) = 100.

Semantics

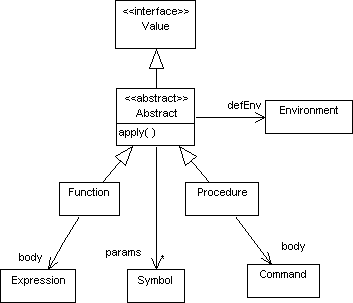
Functions and Procedures are Abstracts. An abstract (also called a closure) contains an abstract apply method, a protected list of parameters, and a protected reference to its defining environment:

Implementation

Here's a sketch of the Abstract class:

abstract class Abstract {
protected Environment defEnv;
protected List<Symbol> params;
abstract Value apply(List<Value> args, Environment env) throw AppError;
}

Notice that I've made a few changes from Alpha. Abstract is now an abstract class rather than an interface. This is because I added the two fields defEnv and params. Of course you will need to provide constructors to initialize these fields.

Here's a sketch of how the Function class might be implemented:

class Function extends Abstract {
Expression body; // = Command in Procedure
Value apply(List<Value> args, Environment env) throw AppError {
1. tempEnv = new Environment with ce = env and de = defEnv
2. put params_i = args_i into tempEnv
3. return body.eval(tempEnv)
}
}

Here's a sketch of how ExpAbstraction might be implemented:

class ExpAbstraction extends SpecialForm {
List<Symbol> params;
Expression body;

static boolean isNext(List<String> tokens) { ... }

static Phrase parse(List<String> tokens) throws AppError {
1. ExpAbstration result = new ExpAbstraction();
2. iteratively call Symbol.parse to init result.params
3. call Expression.parse() to init result.body
4. return result
}

Value eval(Environment env) throws AppError {
return new Function(params, env, body);
}
}

Notice that an instance of ExpAbstraction looks just like an instance of Function. Both contain a parameter list and a body. The similarity is analogous to the similarity between NumberLiteral and NumberValue.