Modules
The Modularity Principle
Programs should be decomposed into a collection of cohesive, loosely coupled modules.
Frames as Bindables
Recall that a frame is a table of bindings.
So far, bindables include:
Number, Boolean, Location, Function, Procedure
The Zeta language extends Epsilon by allowing frames to be bindables. A frame used as a bindable is called a module.
Accessing Nested Bindings
We introduce the following syntax to Zeta:
<Expression> ::= <Qualified Symbol> | etc.
<Qualified Symbol> ::= <Symbol>(.<Symbol>)+
Assume the current frame contains the binding of the symbol f to a frame that contains the binding x = 10. We can access this value as follows:
(+ 3 f.x) // = 13
Note: The idea of a frame as a bindable isn't really so radical. We can think of a frame as a finite function of type:
String -> Object
I call this type of function a dispatch function.
Here's a picture of a frame containing two bindings: m1 and m2. Both are names of modules. The m1 module contains a module binding for m3. The m2 module contains a module binding for m4:
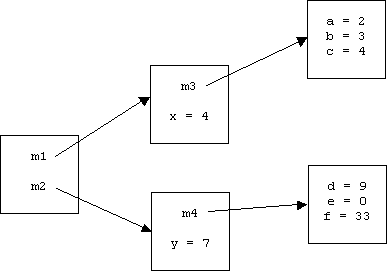
What are the values of the following qualified names:
m1.x =
m1.m3.a =
m2.y =
m2.m4.e =
m1.m3.e =
Declaring Modules in Zeta
Creating a module is similar to creating a function or procedure:
<Expression> ::= (module <Declaration>+) | etc.
When evaluated, a module expression produces a module as its value. As we said earlier, a module is simple a frame, a frame containing the bindings produced by elaborating the declarations inside the module expression. (We are assuming that modules, like abstracts, are statically scoped. Thus, each module contains a pointer to its defining frame.)
Here are some examples of module declarations:
Modules can be objects:
[define myAccount
(module [define balance (var 0)]
[define deposit
(proc (amt)
{assign balance (+ (val
balance) amt)})]
[define withdraw
(proc (amt)
{assign balance (- (val
balance) amt)})]
)
]
Modules can be libraries:
[define utils
(module [define square (fun (x) (* x
x))]
[define cube (fun (x) (* x (square x)))]
[define abs (fun (x) (if (< x 0) (- 0 x) x))]
)
]
Modules can be programs:
[define myProgram
(module [define radius (var 0)]
[define pi 3.14]
[define area (var 0)]
[define main (proc ()
{ begin
{read radius}
{assign area (* (val
radius) (val radius) pi)}
{ print (val area) }
}
]
)
]
Notice that inside a module names of other module members (such as radius, pi, and area) don't need to be qualified.
Here are some examples of how these modules might be used:
{myAccount.deposit 50} // deposit $50 into myAccount
{myAccount.withdraw 20} // withdraw $20 from myAccount
{print (val myAccount.balance)} // prints $30
{print (utils.cube (utils.abs -3)) } // prints 27
{myProgram.main}
Extending Modules
Modules are extensible. We can create new modules by adding bindings to an existing module.
<Expression> ::= (extend <Module> <Declaration>+) | etc.
For example:
[define utils2
(extend utils
[define pi 3.1416]
[define double (fun (x) (+ x x))]
)
]
We can still access the members of utils through utils2:
(utils2.double 5) // = 10
(utils2.square 7) // = 49
(utils2.cube 2) // = 8
We can think of this as a form of inheritance. Utils2 inherits the features of utils. Utils2 may also override (i.e., redefine) any of these features.
Modules as Block Bodies
Modules are expressions, so they can appear as expression block bodies:
(<Let> [<Dec> ... <Dec>] (module <Dec> ... <Dec>))
For example:
(define myAccount
(let [[define balance (var 0)]
(module
[define deposit
(proc (amt)
{assign balance (+ (val
balance) amt)})]
[define withdraw
(proc (amt)
{assign balance (- (val
balance) amt)})]
)
]
In this case balance can only be accessed inside the module:
{myAccount.deposit 50} // deposit $50 into myAccount
{myAccount.withdraw 20} // withdraw $20 from myAccount
{print myAccount.balance} // fails, balance not accessible (NOT)
Packages
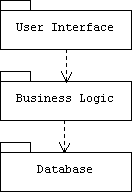
We can represent packages using modules. A package is a named set of related classes, interfaces, and sub-packages. A UML package diagram shows a system's important packages and their dependencies. Packages appear in these diagrams as labeled folders called package icons. A dependency is a dashed arrow pointing from an importer package to an exporter package, and indicates that changes to the exporter package may force changes to the importer package.
For example, the following package diagram indicates that components in the Business Logic package import (use) components defined in the Database package, while components in the User Interface package import components defined in the Business Logic package. Of course some of these components may have been imported by the Business Logic package, so the dependency relationship is transitive.
In a unidirectional dependency the exporter is also called the provider or server, while the importer is called the client. In a bi-directional dependency both packages are called peers:
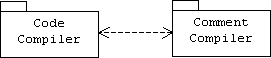
Packages can be implemented in C++ using names spaces:
namespace Database
{
class Query { ... };
class Table { ... };
// etc.
}
namespace BusinessLogic
{
using namespace Database;
class Transaction { ... };
class Customer { ... };
// etc.
}
namespace UserInterface
{
using namespace BusinessLogic;
class DialogBox { ... };
class Menu { ... };
// etc.
}
Placing a package declaration of the form:
package business;
at the top of a .java file puts all of the classes and interfaces declared in the file into the business package.
Exporting and Importing Bindings
Dependencies between Modules
Cohesion, Coupling, and Encumbrance
The cohesion of a module is the degree to which the members of the module are related.
If module M1 depends on (i.e. imports from) module M2, then the coupling degree is the probability that a change in M2 will require a change in M1.
The transitive closure of a module, TC(M), is the set of all modules upon which M depends, including itself.
The encumbrance of a module M is the size of TC(M).
Modules as Function Bodies
Modules are expressions, so they can appear as function bodies:
(fun (x y z ...) (module <Dec> ... <Dec>))
A function that returns a module is called a constructor. For example:
(define makeAccount
(fun (init)
(module
[define balance (var init)]
[define deposit
(proc (amt)
{assign balance (+ (val
balance) amt)})]
[define withdraw
(proc (amt)
{assign balance (- (val
balance) amt)})]
)
)
)
Now we can make lots of accounts:
[define checking (makeAccount 0)
[define savings (makeAccount 20)]
{checking.deposit 30} // deposits $30 in checking account
{savings.withdraw 15} // only $5 left in savings!
Classes, Objects, and Generics
It should be clear by now that objects are modules. We can identify classes with constructors.
We can go one step further and define a function that returns a constructor (class) as a value. We can identify a function like this with a C++ style template or a Java generic.